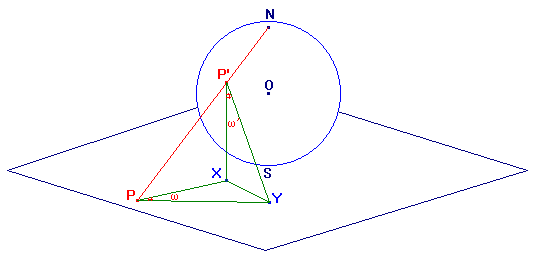
Per dimostrare la conformità prendiamo in esame la figura seguente, dove si è considerato un angolo ω’ sulla sfera, la cui misura è per definizione quella dell’angolo rettilineo formato dalle tangenti agli archi di circonferenza che determinano i suoi lati.

La proiezione sul piano π dell’angolo formato dalle tangenti è l’angolo ω in figura. Si tratta di dimostrare che ω=ω’.

Supponiamo dapprima che X appartenga al piano PNS verticale perpendicolare a π. Allora, poiché i piani NPS e P’XY sono ortogonali, i due triangoli PXY e P’XY sono rettangoli, per cui basta dimostrare che PX=P’X, ossia che il triangolo P’PX è isoscele, come risulta evidente dalla figura che mostra la sezione col piano P’NS (dalle proprietà del cerchio e della sua tangente).

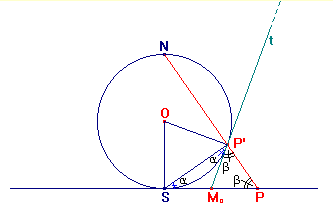
Ne segue in particolare che anche PY=P’Y quindi in ogni caso il segmento di tangente che ha come estremi il punto P’ e l’intersezione della tangente col piano π è congruente alla sua proiezione sul piano π. Da qui segue il risultato generale.