|
Nell'insegnamento della Geometria si possono distinguere due metodi: uno sperimentale (i concetti geometrici fondamentali si acquisiscono attraverso l'esperienza e le loro proprietà sono riconosciute dall'esperienza) e l'altro ipotetico-deduttivo (scienza puramente deduttiva, astratta i cui oggetti sono frutto del solo pensiero). In realtà anche una geometria basata su un sistema puramente logico necessita di essere riconosciuta da tutti e non contraddetta dall'esperienza.
Nello studio delle figure piane, in particolare delle relazioni di equivalenza, congruenza, uguaglianza, occorre costruire un percorso didattico motivante per l'allievo senza rinunciare alla correttezza formale. La manipolazione, l'esplorazione, la ricerca di proprietà, la formulazione di congetture, renderanno vive le lezioni di geometria andando via via a costruire le basi per uno studio assiomatico che a livello di scuola media si dimostra ancora prematuro. Nel corso degli studi sarà comunque importante far percepire che ogni teoria è costruita attraverso un laborioso cammino, fatto di ipotesi differenti, imprecisioni, errori, in un clima di collaborazione e competizione. Si giungerà quindi a capire che non esiste una matematica ma più matematiche ciascuna delle quali si fonda su un insieme di assiomi dai quali si deducono con procedimento ipotetico-deduttivo, i teoremi; ognuna di esse potrà considerarsi vera se, ciascuna teoria sulla quale viene edificata, non presenta contraddizioni, se coerente, ugualmente valida. |
|
Proviamo a considerare l'esempio dell'uguaglianza (estensiva) di grandezze: quando si considerano solo segmenti o angoli la congruenza, la sovrapponibilità e l'uguaglianza estensiva (o equivalenza) si identificano. Ma per le superfici poligonali? Euclide, considerando il concetto di area come primitivo, fonda la sua teoria dell'equivalenza dei poligoni su alcuni postulati:
Ma perché l'uguaglianza di estensione possa essere oggetto di studio rigoroso, è necessaria un'analisi approfondita, che manca in Euclide e fu compiuta soltanto in tempi recenti. Diversi furono i matematici che si impegnarono a costruire una teoria della equivalenza di poligoni fino a giungere a dimostrare
E da questi derivano i teoremi:
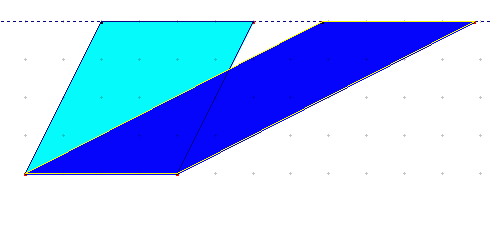
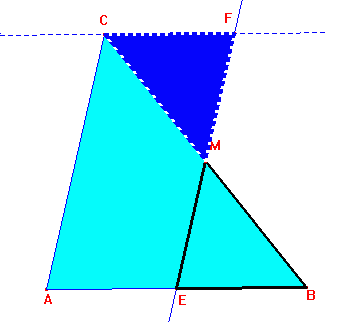
1a Due parallelogrammi aventi uguali le basi e le altezze relative, sono equivalenti
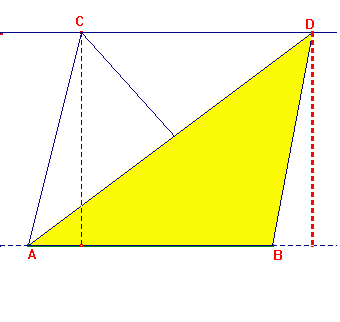
2a. Due triangoli di base e altezza uguali sono equivalenti
|