![]()
Orologio con due ore.
Prendiamo un orologio con due ore: 0 e 1. (Abbiamo scritto 0 e 1 invece di 1 e 2 perchè i possibili resti nella divisione per 2 sono 0 e 1; se preferite 1 e 2 è lo stesso purchè 1 = 1 e 2 = 0). Se facciamo la somma delle ore con questo orologio viene:
0 + 0 = 0 (mod 2)
1 + 0 = 0 + 1 = 1 (mod 2)
1 + 1 = 0 (mod 2)
Tutto regolare tranne l'ultima uguaglianza, ma se guardiamo all'orologio, anche questa torna.
Un altro modo di vedere le cose è il seguente: n = 0 (mod 2) se e solo se n è pari; invece n = 1 (mod 2) se e solo se n è dispari.
-la somma di due numeri pari è un numero pari (cioè 0+0=0 (mod 2))
-la somma di un numero pari e di un numero dispari è un numero dispari (cioè 1+0=1 (mod 2))
-la somma di due numeri dispari è un numero pari (cioè 1+1=0 (mod 2)).
Possiamo riassumere la legge dell'addizione dei numeri dell'orologio con due ore (in matematichese: "dei numeri modulo 2") con la seguente tabella:
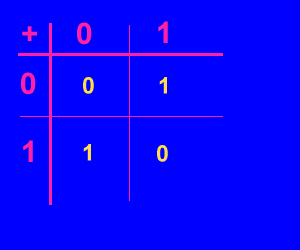
Passiamo ora alla moltiplicazione. Abbiamo:
0x0 = 0 (mod 2), 1x0 = 0x1 = 0 (mod 2) e 1x1 = 1 (mod 2)
Infatti il prodotto di due numeri pari è un numero pari; il prodotto di un numero pari con un numero dispari è un numero pari; il prodotto di due numeri dispari è un numero dispari.
Abbiamo quindi la seguente tabella per la moltiplicazione: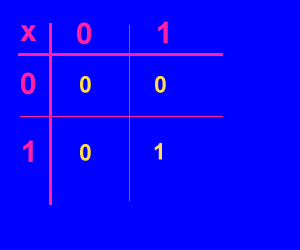
![]()
Orologio con quattro ore.
Questa volta il nostro orologio ha quattro ore: 0, 1, 2, 3 (che sono i possibili resti nella divisione per 4).
Abbiamo: 0+0 = 0 (mod 4); 0+1 = 1 (mod 4); 0+2 = 2 (mod 4); 0+3 = 3 (mod 4); e poi:
1+1 = 2 (mod 4); 1+2 = 3 (mod 4); 1+3 = 0 (mod 4), 2+2 = 0 (mod 4).
Le cose notevoli sono: 1+3 = 0 (mod 4) e 2+2 = 0 (mod 4). Infatti 1+3 = 4 e il resto nella divisione di 4 per 4 è 0. Stessa cosa per 2+2.
Aggiungerei: per fortuna che è così!!
Infatti guardiamo alla tabella dell'addizione "modulo 4": 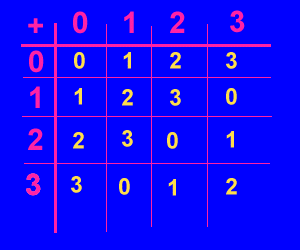
Vediamo che grazie proprio a queste stranezze, l'addizione verifica due proprietà che la solita addizione (con numeri interi positivi e negativi) verifica, cioè:
- esiste lo zero 0 che verifica: n+0 = 0+n = n per ogni numero n (aggiungere 0 non cambia nulla, si dice che 0 è "elemento neutro" per l'addizione)
- per ogni numero n esiste un numero -n tale che: n + (-n) = (-n) + n = 0 (si dice che -n è il "simmetrico" di n per l'addizione. Per esempio -2 è il simmetrico di 2 (e 2 è il simmetrico di -2).
Anche i nostri numeri dell'orologio con 4 ore godono di queste proprietà:
- l'elemento neutro è sempre lo zero.
- ogni elemento ha un simmetrico: il simmetrico di 1 è 3 (e viceversa); il simmetrico di 2 è 2.
Siccome i nostri numeri, come quelli "normali", verificano le proprietà:
- per ogni n e per ogni m: n + m = m + n ("commutatività")
- per ogni n, per ogni m e per ogni t: t + (n +m) = (t + n) + m ("associatività")
vediamo che malgrado (o grazie) alle sue stranezze, l'addizione dei numeri modulo 4 è strutturalmente uguale a quella dei numeri normali (i matematici dicono l'addizione conferisce a questi numeri una struttura di "gruppo"; la nozione di "gruppo" è fondamentale oggigiorno in matematica, ma qui siamo già molto avanti ...)
 Attenzione!!!
Le cose non vanno così bene con la moltiplicazione
Attenzione!!!
Le cose non vanno così bene con la moltiplicazione
Infatti abbiamo: 2x2 = 0 (mod 4), perchè 2x2 = 4 è il resto nella divisione di 4 per 4 è 0.
Questo non succedde con i numeri normali: se axb = 0, allora a = 0 o b = 0.
La tabella della moltiplicazione dei numeri modulo 4 è: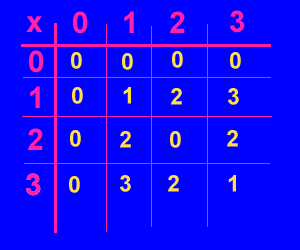
Vediamo che non esiste nessun numero n tale che: 2xn = 1 (mod 4).
Osserviamo però che: 3x3 = 1 (mod 4)
Invece con i numeri normali (ma considerando anche le frazioni) abbiamo che: per ogni n diverso da 0, esiste 1/n tale che: nx(1/n) = 1 (questo è vero anche se n = a/b è una frazione, in questo caso 1/n = b/a). Come per la somma dei numeri interi positivi e negativi, la moltiplicazione conferisce alle frazioni (escluso 0) una struttura di "gruppo" (l'elemento neutro è 1 = 1/1; il simmetrico di n è 1/n).
La moltiplicazione NON conferisce una struttura di "gruppo" ai numeri modulo 4 (escluso lo 0), perchè 3 ha un simmetrico (3x3 = 1 (mod 4)) ma 2 no. Questa volta c'è una differenza strutturale, ben illustrata dal fatto che 2x2 = 0 (mod 4) (se 2 avesse un simmetrico, 2*, questo non sarebbe possibile: 2*x(2x2) = 2*x0, ma 2*x(2x2) = (2*x2)x2 = 1x2 = 2 e si avrebbe 2 = 0, assurdo).
![]()
Orologi con n ore.
Come già detto possiamo considerare orologi con un numero (intero) n, qualsiasi di ore. Il nostro orologio avrà n ore: 0, 1, 2, ...., (n-1) (sono i resti possibili nella divisione per n). Non è troppo difficile convincersi che per l'addizione le cose vanno sempre bene (il simmetrico di 1 è n-1; quello di 2, n-2; quello di 3, n-3; ecc...).
Per la moltiplicazione possono esserci dei problemi. Si dimostra (al primo anno di università) che la moltiplicazione si comporta "bene" se, e solo se, n è un numero primo.
A titolo d'esempio la tabella della moltiplicazione per i numeri modulo 5 è:
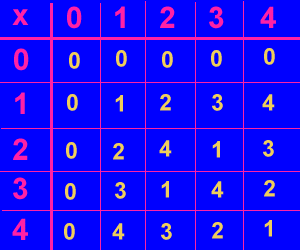
e potete verificare che se t è diverso da zero, esiste sempre t* tale che: txt* = 1 (mod 5) (cioè in ogni riga corrispondente a t diverso da 0, compare 1). Quindi, in particolare, se axb = 0 (mod 5), allora a = 0 o b = 0.
Da cui, ancora una volta, l'importanza di essere primo!