I "numeri dell'orologio".

La lancetta delle ore dell'orologio punta sulle due: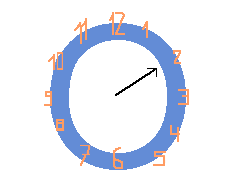

12 ore dopo, la lancetta punta sempre sulle 2 (abbiamo fatto un giro completo). Quindi aggiungere 12 non cambia niente al numero delle ore: 2 + 12 = 2.

I matematici, per indicare che stanno contando le ore, scrivono: 2 + 12 = 2 (mod 12)

Anzi, se facciamo un numero qualsiasi, n, di giri, la lancetta punterà sempre sulle 2: 2 + 12n = 2 (mod12)

Invece 14 ore dopo la lancetta punterà sulle 4: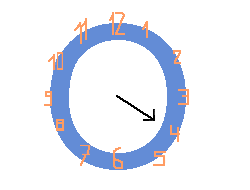

Strano però perchè: 2 + 14 = 16 e non 4?!

In realtà non è cosi strano perchè: 2 + 14 = 2 + (2 + 12) = (2 + 2) + 12 = 4 + 12 = 4 (mod 12)

Stiamo contando "modulo 12"

Se aggiungiamo 47, cosa succedde?

Per vederlo si divide 47 per 12: 47 = 3x12 + 11. Aggiungere 47 è come aggiungere 11, quindi: 11 + 2 = 13, ma 13 = 1 + 12. Finalmente 47 + 2 = 1 (mod 12).

Vediamo che per il numero delle ore, quello che importa non è il numero n ma il suo resto nella divisione per 12. Ci sono 12 resti possibili: 0, 1, 2, ..., 11. Sono le ore dell'orologio (12 = 0 (mod 12))

Altri orologi.

Possiamo considerare orologi con un numero diverso di ore, ecco, per esempio, un orologio con 7 ore (come i giorni della settimana)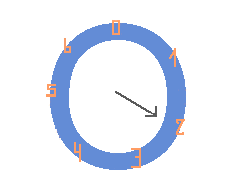

Con questo orologio: 2 + 20 = 1 (mod 7)

Scriviamo (mod 7) per indicare che stiamo usando un orologio con 7 ore.

Infatti: 20 = 2.7 + 6 = 6 (mod 7) e 2 + 6 = 8 = 1 (mod 7)

(Se 1 = Lunedi, 2 = Martedi, ..., 0 = Domenica e se aggiungo 20 giorni a un Martedi, viene un Lunedi.)

Chiaramente possiamo considerare orologi con un numero n qualsiasi di ore.

Per riassumere:

• La scrittura a = b (mod n) significa che a e b hanno lo stesso resto nella divisione per n (dopo avere aggiunto a ore, la lancetta dell'orologio con n ore punterà alla stessa ora che se io avessi aggiunto b ore). Dire che a e b hanno lo stesso resto nella divisione per n significa che a-b è divisibile per n (a = kn+r, b=tn+r, 0<=r<n, quindi a-b=n(k-t))
• Dire che a = r (mod n), con 0<= r <n, è equivalente a dire che a è della forma a = kn+r (un multiplo di n più r).

Per concludere: I "numeri dell'orologio" sono (più o meno) come i numeri normali: possiamo sommarli e moltiplicarli, però certe volte queste operazioni si comportano in modo strano...

                                                        Ritorno alla pagina principale "Congruenze"