
ProbleMATEMATICAmente - Marzo 2001
Daniele Urzì, classe III B, liceo scientifico "G.Galilei" (Catania)
Nella Catottrica Erone Alessandrino si occupa del problema di determinare il percorso di minima lunghezza che un raggio luminoso uscente da una sorgente P deve compiere per raggiungere uno specchio piano e poi l’occhio Q di un osservatore. Possiamo riformulare il problema in questo modo: dati due punti P e Q, giacenti in una stessa parte di piano rispetto ad una retta t, trovare il percorso minimo da P a Q toccando un punto R di t. Erone risolse così il problema: si unisca il punto P', simmetrico di P rispetto a t, con Q determinando il punto R d’intersezione di P’Q con t. E’ facile dimostrare che PR+RQ è il percorso minimo richiesto (fig.1): se V è un punto qualunque di t, si osservi che è PR=P’R e VP=VP’; da questo segue che PR+RQ=P’R+RQ e VP+VQ=VP’+VQ; ricordando che ogni lato di un triangolo è minore della somma degli altri due, si ha, relativamente al triangolo VQP’, la relazione P’Q<VQ+VP’, per cui PR+RQ è sempre minore di VP+VQ . Erone fa notare che l’angolo di incidenza PRV è uguale all’angolo di riflessione QRT (gli angoli QRT, VRP’ sono uguali perché opposti al vertice R, gli angoli PRV, VRP’ sono uguali perché t è la bisettrice dell’angolo al vertice del triangolo isoscele PRP’; per la proprietà transitiva è QRT=PRV).

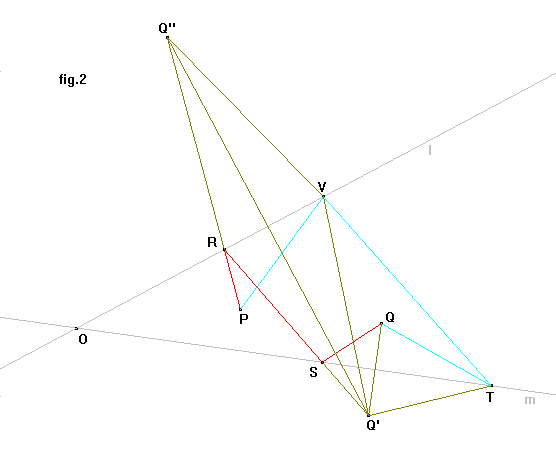
Nel testo Che cos’è la matematica? di Courant e Robbins il problema viene generalizzato considerando due rette qualsiasi l ed m e due punti P e Q come nella figura 2. Sia Q’ il simmetrico di Q rispetto ad m e Q’’ il simmetrico di Q’ rispetto ad l; chiamiamo R ed S rispettivamente le intersezioni di PQ’’ con l e RQ’ con m; la spezzata PRSQ è il percorso minimo richiesto. Lo dimostriamo: siano V e T due punti qualunque rispettivamente di l ed m; dalle relazioni SQ=SQ’ , QT=Q’T seguono le altre due RS+SQ=RS+SQ’=RQ’’ [Nota di probleMATEMATICAmente: quest'ultima uguaglianza dipende dal fatto che RQ'=RQ''] e VT+QT=VT+Q’T; inoltre è VT+Q’T>VQ’=VQ’’ e VP+VQ’’>PQ’’, perciò, essendo VT+Q’T>VQ’’, è ovvia la disuguaglianza VP+VT+Q’T>PQ’’ o anche PR+RS+SQ<VP+VT+TQ, come volevasi dimostrare.
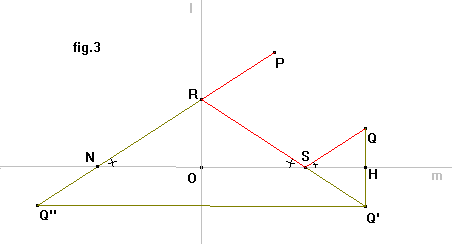
Se l ed m sono perpendicolari, i segmenti RP e SQ sono paralleli: gli angoli QSH, RSN come abbiamo dimostrato sono uguali e il triangolo NRS è isoscele su base NS, quindi per la proprietà transitiva gli angoli RNS, QSH, corrispondenti generati dalle rette PN e QS tagliate dalla trasversale m, sono uguali, da cui segue che le rette PR e SQ sono parallele.
Si può facilmente dimostrare che i segmenti PR e SQ sono paralleli anche quando l ed m sono parallele. Infine, volendo trovare il percorso minimo toccando prima m e poi l, il punto Q’ deve essere simmetrico di Q rispetto a l e Q’’ simmetrico di Q’ rispetto a m.