FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema

Dal vertice A di un triangolo ABC (vedi figura) condurre la retta parallela a BC e su di essa riportare, da parti opposte rispetto ad A, i segmenti AM e AN entrambi congruenti ad AC.

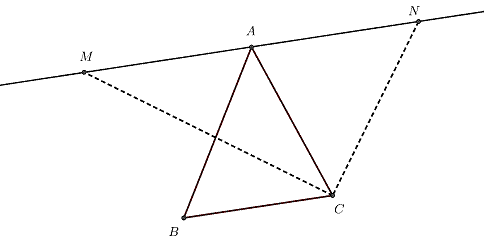
a) Dimostrare che i triangoli ACM e ACN sono equivalenti.

b) Dimostrare che CM e CN sono le bisettrici dei due angoli, interno ed esterno, in C del triangolo ABC.

c) Dimostrare che il triangolo MCN è rettangolo in C.

Giustificare tutte le risposte.

Commento alle soluzioni ricevute

Sono giunte sei risposte, tre provenienti da due diversi Licei scientifici, due da due diversi Licei Classici e una da un Liceo Linguistico.

Il problema poneva tre quesiti relativi alla stessa figura: nel primo si chiedeva di dimostrare l’equivalenza di due triangoli, nel secondo di dimostrare che due segmenti aventi come estremo comune un vertice di un triangolo erano le bisettrici dei due angoli, interno ed esterno, individuati da tale vertice e nell’ultimo di dimostrare che un triangolo risultante dalla costruzione effettuata era rettangolo.

Alla prima domanda tutti, tranne uno, rispondono in modo sostanzialmente corretto, mentre tutti arrivano a risolvere il secondo e il terzo quesito, sia pure con qualche imprecisione.

Ci preme sottolineare innanzi tutto due aspetti importanti della pratica geometrica da tenere presenti nei futuri elaborati: 1) stabilito che, in generale, si indicano con una lettera latina maiuscola i punti caratteristici di una figura (vertici, punti di intersezione, ecc.) e con una terna di lettere un angolo (con il vertice al centro della terna), diventa di conseguenza improprio indicare un angolo di particolare ampiezza con la sola lettera R, se si tratta di un angolo retto, o con la sola lettera P, se si tratta di un angolo piatto; 2) non è accettabile che si usino lettere per indicare punti di cui non è stata precisata in alcun modo la costruzione anche se poi compaiono nelle figure inserite nella soluzione. Infine, come ormai da troppo succede, vogliamo ribadire la necessità di distinguere tra un ente geometrico e la sua misura (in particolare tra un angolo e la misura della sua ampiezza e tra un segmento e la misura della sua lunghezza).

Un’ultima importante considerazione: la dimostrazione di una data implicazione non comporta necessariamente la validità dell’implicazione inversa, che quindi richiede, per la sua validità, una dimostrazione autonoma. In particolare il fatto che in un triangolo rettangolo la mediana relativa all’ipotenusa sia congruente a metà dell’ipotenusa stessa non implica automaticamente che se in un triangolo la mediana relativa ad uno dei lati è congruente alla metà di quel lato il triangolo sia rettangolo (proprietà comunque vera ma che richiede una dimostrazione autonoma).

Sono pervenute risposte dalle seguenti scuole:

• LC “G. Asproni”, Nuoro (NU)

• LS, Scienze applicate, “G. Terragni”, Olgiate Comasco (CO)

• LS “G. Galilei”, Adria (RO)

• Liceo “Stabili-Trebbiani”-indirizzo Linguistico, Ascoli Piceno (AP)

• LC “G. Parini”, Milano (MI)

NOTA. Nelle soluzioni riportate, le correzioni, le aggiunte o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

Come di consueto presentiamo tutti i commenti riuniti in questo unico file pdf (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni, le aggiunte o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

---------

Il gruppo di lavoro che gestisce FLATlandia è composto da:

- Ercole CASTAGNOLA - NRD Università di Napoli “Federico II”

- Giuliano MAZZANTI - Docente di Geometria, Università di Ferrara

- Valter ROSELLI - Ricercatore, Dipartimento di Matematica, Università di Ferrara

- Luigi TOMASI - Insegnante di Matematica, Liceo Scientifico Galilei Adria (RO).

| Home Page Cabri | Torna a FLATlandia | Archivi |