FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema:

Un rettangolo è suddiviso in tre triangoli rettangoli e un pentagono come mostrato in figura, dove sono anche indicate le lunghezze di alcuni segmenti.

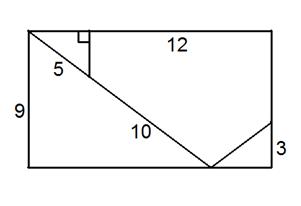
1) Trovare le misure incognite di tutti i lati dei triangoli e del pentagono suddetti.

2) Trovare la misura del lato del quadrato equivalente al rettangolo dato e costruire tale quadrato con riga e compasso.

3) Verificare che è possibile ricomporre i quattro “pezzi” che formano il rettangolo iniziale in modo da ottenere il quadrato di cui al punto 2.

Motivare le risposte.

Commento

Abbiamo ricevuto venticinque risposte così suddivise: due da classi prime delle Scuole Superiori, tredici da classi seconde e quattro da classi terze, sempre di Scuole Superiori e infine in due risposte, ancora di Scuole Superiori, non è precisata la Classe di appartenenza; inoltre abbiamo ricevuto tre risposte da classi di Scuola Media, due di Classi terze e una di Classe seconda, e ancora in una risposta non viene citata né la Classe, né la Scuola.

Il problema poneva tre domande (tra loro collegate): nel primo quesito si chiedeva di determinare la misura di alcuni segmenti presenti nella figura iniziale costituita da un rettangolo suddiviso, tramite opportuni segmenti, in tre triangoli e in un pentagono; nel secondo si chiedeva di costruire con riga e compasso un quadrato equivalente al rettangolo iniziale e nel terzo quesito si chiedeva di verificare la possibilità di riordinare la suddivisione iniziale in modo da formare il quadrato citato nel secondo quesito.

Quasi tutti “intuiscono” la soluzione per i diversi quesiti, ma pochi seguono una strada geometricamente corretta. Innanzi tutto occorre chiarire che il fatto di intuire che un triangolo rettangolo abbia come misure dei lati una terna pitagorica non esime dalla necessità di fornire una dimostrazione di tale proprietà. Inoltre vale la pena di sottolineare che se un triangolo rettangolo ha due lati la cui lunghezza è espressa da un numero intero, questo non implica che anche il terzo lato abbia lunghezza intera. Si nota poi che la costruzione con riga e compasso richiesta dal secondo quesito è quasi sempre stata affrontata con software di Geometria Dinamica che hanno al loro interno già implementate alcune delle costruzioni necessarie (come condurre le rette parallela e perpendicolare ad una data retta passanti per un dato punto). Infine vogliamo ribadire la necessità di fornire una opportuna motivazione per la “ricomposizione” prevista dal terzo quesito.

Per concludere alcune raccomandazioni e richieste per il futuro:

1) non verranno più accettate soluzioni che non riportino chiaramente il nome dei risolutori e la classe di provenienza;

2) non saranno prese in considerazione elaborati con la scrittura della soluzione all’interno del file contenente la figura, in quanto risulta poi impossibile utilizzare tale file per la pubblicazione in rete.

È inoltre auspicabile un’attenta rilettura della soluzione prima del relativo invio per evitare di dover correggere testi scritti con una scarsa accuratezza che a volte ne impedisce la comprensione.

Sono pervenute risposte dalle seguenti scuole:

LS “Alfano da Termoli”, Termoli (CB)

LS “Don Milani”, Montichiari (BS)

LS Scienze Applicate “B. Russell”, Cles (TN)

LS “E. Torricelli”, Faenza (RA)

Liceo delle Scienze Umane presso LC “Mamiani”, Pesaro (PU)

LC “Chris Cappell College”, Anzio (RM)

LS “G. Aselli”, Cremona (CR)

SM “P. Neruda”, Roma (RM)

SM “G.B. Tiepolo”, Milano (MI)

SM “Dimesse”, Udine (UD)

Come di consueto presentiamo tutti i commenti riuniti in questo unico file PDF (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

| Home Page Cabri | Torna a FLATlandia | Archivi |