FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

Il testo del problema
 

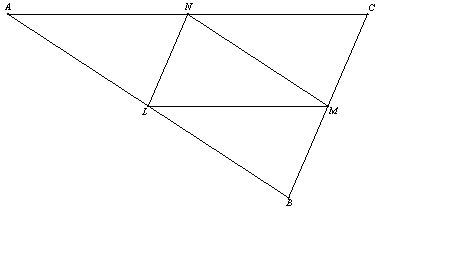
È dato il triangolo LMN. Dare una costruzione di un triangolo ABC, avente come punti medi dei suoi lati L, M, N.

a) Dimostrare che tale triangolo è unico.

b) Provare che ABC ed LMN sono triangoli simili.

c) Trovare il rapporto tra le aree dei triangoli ABC ed LMN.

Commento

Sono giunte dieci risposte, tutte provenienti da classi del primo biennio di Licei Scientifici. In alcuni casi si tratta di singoli studenti o gruppi di studenti all’interno di una classe, in altri di una classe intera. Desta qualche perplessità il fatto che tutte le risposte provengano dallo stesso tipo di scuola, cioè il Liceo Scientifico.

Il problema richiedeva la costruzione di un triangolo, partendo da un triangolo dato e, relativamente a tale costruzione, poneva tre quesiti: nel primo si chiedeva di dimostrare l’unicità del triangolo avente le proprietà richieste; nel secondo di dimostrare la similitudine tra il triangolo dato e il triangolo costruito e nell’ultimo di determinare il valore del rapporto tra le aree dei due triangoli.

Tutti rispondono in modo sostanzialmente corretto ai quesiti (in una sola risposta non viene preso in esame il primo quesito). Tuttavia in molte risposte permane la confusione tra una grandezza geometrica e la sua misura (ad esempio, tra un angolo e la sua ampiezza o tra un segmento e la sua lunghezza).

La dimostrazione dell’unicità del triangolo richiesto è incompleta in quasi tutte le risposte. Tutti iniziano a costruire le rette parallele ai lati passanti rispettivamente per i vertici opposti. Si afferma poi che la parallela è unica, citando il postulato della parallela. È da notare che questo ragionamento dimostra soltanto che il triangolo costruito in questo modo, mandando le parallele ai lati, è unico. Ma ci sarà un altro modo di costruire un triangolo che soddisfa alle richieste del problema? Molti non si pongono questa domanda.

Ancora una raccomandazione: evitare assolutamente di utilizzare il formato pdf per la soluzione da inviare, in quanto risulta poi estremamente difficile ritagliare le parti della soluzione che vengono poi pubblicate. 

Sono pervenute risposte dalle seguenti scuole:

LS “Pitagora”, Rende (CS)

LS “Don Milani”, Montichiari (BS)

LS “Aristosseno”, Taranto

LS “A. Banfi”, Vimercate (MI)

LS “F. Masci”, Chieti

LS “E. Majorana”, Pozzuoli (NA)

LS “T. Gullace”, Roma

LS “C. Cafiero”, Barletta (BA).

Come di consueto presentiamo tutti i commenti riuniti in questo unico file pdf (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono indicate le parti omesse.

| Home Page Cabri | Torna a FLATlandia | Archivi |