FLATlandia - Problema di Maggio 2010

Il testo del problema:
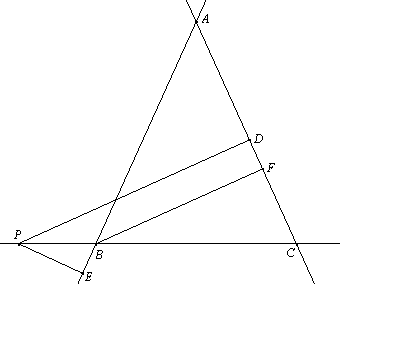
Sia ABC un triangolo isoscele (AB e AC sono i lati uguali). Sul prolungamento di BC dalla parte di B si prenda un punto P e da esso si traccino le perpendicolari PD e PE rispettivamente alle rette dei lati AC e AB. Detta BF l'altezza del triangolo ABC relativa al lato AC, quale relazione esiste tra i segmenti PD, PE e BF ?
Se il punto P è interno al lato BC tale relazione sussiste ancora ? In caso negativo trovarne un'altra.

Commento (scarica qui il commento completo in un unico file pdf )

Abbiamo ricevuto quattordici (!) risposte così suddivise: una da un Educandato Statale, dieci dal biennio delle Scuole Superiori (sei da studenti di una stessa prima) e tre dal triennio delle Scuole Superiori (due del III anno e una addirittura del V anno [che dovrebbe essere considerata “fuori gara”]).

Il problema poneva due domande: nel primo quesito si chiedeva di determinare la relazione esistente tra le lunghezze di tre segmenti indicati in figura; nel secondo quesito si chiedeva di verificare la sussistenza o meno della stessa relazione in seguito alla modifica della posizione di uno dei punti della precedente figura e, in caso di risposta negativa, di trovare la nuova relazione esistente tra detti segmenti.

Se da una parte constatiamo con soddisfazione la grande partecipazione alla soluzione dei problemi di Flatlandia, dall’altra dobbiamo rilevare una certa mancanza di accuratezza nella stesura delle risposte e, in alcuni casi, una scarsa attenzione alla costruzione delle figure, anche se i problemi connessi con l’avvicinarsi della conclusione dell’anno scolastico possono in parte giustificare una  elaborazione “frettolosa”. Riteniamo comunque opportune ribadire alcune norme da seguire nella stesura delle soluzioni:
a) per la scrittura del testo occorre utilizzare un editor compatibile con Word 97-2003 (quindi evitare di inviare file con estensione docx); in particolare non possono essere accettati testi scritti a mano e poi copiati con lo scanner;
b) prima di inserire le figure, controllare che le etichette siano posizionate in modo chiaro in modo da non rendere le figure troppo “affollate” e quindi di difficile lettura [controllare anche che la figura sia aderente al testo del problema ed evitare l’uso del “disegnatore” di Word per la costruzione della figura];
c) se si decide di scrivere la soluzione come la dimostrazione di un teorema (con Ipotesi e Tesi) occorre esplicitare chiaramente anche la Tesi [ad esempio, non si può scrivere in modo generico “la relazione tra i lati ..."].

Il problema di maggio conclude l’impegno di “lavoro” di quest’anno scolastico che ha visto la “rinascita” di Flatlandia.
Cogliamo l’occasione per ringraziare tutti coloro che hanno partecipato a questa rinnovata attività.
Per il prossimo anno scolastico ci auguriamo sia di ritrovare i nostri amici fedeli che di vedere aggiungersi nuovi partecipanti a condividere il progetto Flatlandia.

Sono pervenute risposte dalle seguenti Scuole:

• Educandato Statale “Agli Angeli”, Verona (VR)

• LS “A. Banfi”, Vimercate (MI)

• LS “P. Paleocapa”, Rovigo (RO)

• LS “T. Gullace Talotta”, Roma

• LS “B. Russell”, Roma

• LS "Pitagora", Rende (CS)

• LS “Aristosseno”, Taranto (TA)

• IIS “L. Cremona”, Milano (MI)