 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Marzo/Aprile 2009
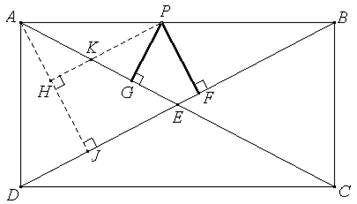
È dato un rettangolo ABCD. Da un punto P del lato AB si conducano i segmenti di perpendicolare PF e PG alle due diagonali AC e BD rispettivamente.
1) Dimostrare che la somma delle lunghezze dei segmenti PF e PG è costante al variare di P su AB.
2) Se P si trova sul prolungamento di AB, la proprietà suddetta (riferita ora alle rette sostegno delle due diagonali) è ancora valida? Se la risposta è affermativa dimostrarlo, in caso contrario modificare opportunamente la proprietà relativa alle lunghezze dei segmenti PF e PG.
Commento
Il problema poneva due quesiti che riguardavano sostanzialmente la stessa
figura: nel primo si chiedeva di dimostrare il permanere di una certa proprietà
al variare della posizione di un punto appartenente a un dato segmento; nel
secondo si chiedeva se tale proprietà era ancora valida nel caso in cui il punto
in questione fosse libero di spostarsi sul prolungamento del precedente segmento
e, in caso di risposta negativa, di modificare opportunamente la proprietà in
esame.
Dobbiamo subito rilevare una certa mancanza di accuratezza nella stesura delle
risposte e, in alcune di queste, una scarsa attenzione alla simbologia impiegata
[forse comincia a farsi sentire la stanchezza di fine anno scolastico!].
In alcune delle risposte pervenute viene dimostrata in modo sostanzialmente
corretto la costanza della somma (punto 1) o della differenza (punto 2) delle
due lunghezze; in alcune viene precisato anche il valore.
Si devono rilevare diverse imprecisioni, sia geometriche che di linguaggio, e
l’utilizzo di certe relazioni geometriche che dovrebbero essere dimostrate.
Inoltre è presente una certa confusione tra un segmento e la relativa lunghezza,
che comporta un passaggio un po’ troppo disinvolto dalla congruenza di segmenti
all’uguaglianza delle loro lunghezze.
Ci preme sottolineare che dire che “un punto sta fuori di un certo segmento” non
equivale ad affermare che tale punto appartiene al prolungamento del segmento in
questione. Inoltre in alcune risposte si afferma che le diagonali di un
rettangolo si dimezzano deducendo che i triangoli formati dalle semidiagonali
sono isosceli: ovviamente occorre precisare anche che le diagonali sono uguali.
Infine in due risposte l’infelice simbologia impiegata ha reso il testo
praticamente illeggibile.
Sono pervenute risposte dalle seguenti scuole:
Si allega QUI il documento PDF con le risposte
NOTA: Nelle soluzioni
riportate, le correzioni o i commenti sono scritti fra parentesi quadre. Con
doppia parentesi quadra vengono indicate le parti omesse.
| Home Page Cabri | Torna a FLATlandia | Archivi |