 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Marzo 2008
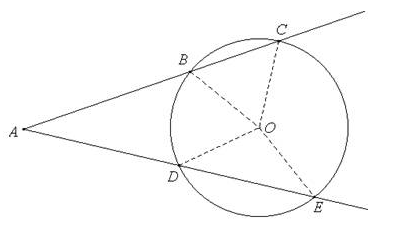
Da un punto A, esterno a una circonferenza di centro O, vengono tracciate due semirette che intersecano la circonferenza rispettivamente nei punti B, C e D, E.
1) Che relazione sussiste tra l’ampiezza dell’angolo ÐA e le ampiezze degli angoli ÐCOE e ÐBOD?
2) Se la distanza tra il punto A e il centro O della circonferenza è uguale al diametro, trovare il valore massimo dell’ampiezza dell’angolo ÐA.
Motivare le risposte.
Commento
Abbiamo ricevuto cinque risposte così suddivise: tre dal biennio delle Scuole Superiori (e due di queste hanno come autori due diversi studenti di una stessa classe) e due dal triennio delle Scuole Superiori (sempre III anno). Il problema poneva due domande (tra loro collegate): nel primo quesito si chiedeva di individuare la relazione esistente tra le ampiezze di tre angoli nella figura proposta; nel secondo quesito si chiedeva di stabilire, in una situazione particolare, il valore dell’ampiezza massima di uno degli angoli individuati nel primo quesito.
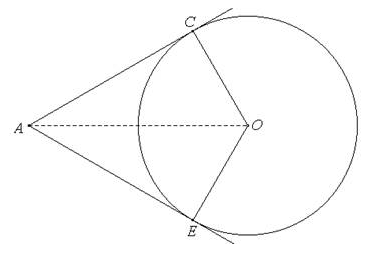
In tutte le risposte pervenute viene risolto in modo sostanzialmente corretto il primo quesito (segnaleremo caso per caso le eventuali imprecisioni). Per il secondo quesito, una sola risposta è da ritenere sufficientemente aderente alle richieste del problema. Innanzi tutto ci preme sottolineare che, indipendentemente dalla distanza del punto A dal centro della circonferenza (purché A rimanga esterno a essa) il valore massimo dell’ampiezza dell’angolo ÐA si raggiunge quando le due semirette diventano tangenti alla circonferenza; la particolare distanza tra i punti A e O prevista dal problema aveva lo scopo di evitare nella risposta l’uso delle funzioni trigonometriche (e questo ha contribuito a non considerare accettabile la risposta fornita da una terza superiore che, avendo utilizzato la prima versione del testo del problema, prevedeva l’uso della funzione arcoseno). La situazione che prevede il secondo quesito è quella rappresentata nella figura seguente
Infine [come osservazione finale divertente], in una risposta al secondo quesito viene citato, come motivazione per la congruenza di due triangoli, il “teorema del triangolo rettangolo”: l’unico teorema riguardante i triangoli rettangoli di cui basta citare il nome con cui è storicamente conosciuto è il “teorema di Pitagora”, di tutti gli altri è bene esplicitare almeno parte dell’enunciato.
Sono pervenute risposte dalle seguenti scuole:
ITCG “Ruffini”, Imperia (IM)
ITCG “E. Majorana”, Castrolibero (CS)
LS “Pitagora”, Rende (CS)
LS “Aristosseno”, Taranto (TA)
Si allega
QUI il documento
PDF con le risposte
NOTA. Nelle soluzioni riportate, le correzioni o i
commenti sono scritti fra parentesi quadre. Con doppia parentesi quadra vengono
indicate le parti omesse.
| Home Page Cabri | Torna a FLATlandia | Archivi |