FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Gennaio 2008

IL TESTO DEL PROBLEMA

1) In un triangolo rettangolo ABC indichiamo con CF la mediana relativa all’ipotenusa AB, con CE la bisettrice dell’angolo ACB (col punto E appartenente all’ipotenusa AB) e con CD l’altezza relativa ad AB. Dimostrare che l’angolo DCE è congruente all’angolo ECF (ÐDCE @ ÐECF).

2) Tracciare la circonferenza circoscritta al triangolo ABC e considerare i punti G, H, I, rispettivamente simmetrici di C nelle simmetrie di centro D, E, F. Quali proprietà si deducono per i  punti G, H, I?

3) La proprietà dimostrata nel punto 1) vale anche se il triangolo non è rettangolo?

 

 


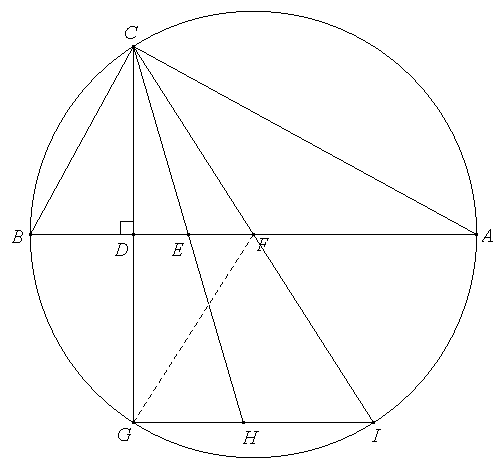
Commento

Abbiamo ricevuto sei risposte così suddivise: una proveniente da una Scuola Media, tre dal biennio delle Scuole Superiori, e due dal triennio delle Scuole Superiori (sempre III anno). Il problema poneva tre domande (tra loro collegate): nel primo quesito si chiedeva di dimostrare la congruenza (o, se si preferisce, l’uguaglianza) di due angoli; nel secondo di determinare di quali proprietà godeva una terna di punti, di cui si dava la costruzione geometrica e nel terzo di verificare se la proprietà dimostrata nel primo punto, a proposito dei triangoli rettangoli, risultava valida anche per altri triangoli.

In tutte le risposte pervenute viene risolto correttamente il primo quesito, ma ci teniamo a sottolineare che in una di queste risulta poco curato l’aspetto linguistico: sarebbe auspicabile in futuro una maggiore cura nell’elaborazione del testo. Per il secondo quesito, solo alcuni rispondono in modo sostanzialmente corretto utilizzando le similitudini tra triangoli o  un’opportuna omotetia. [Vogliamo, inoltre, ricordare che un fascio di rette parallele è costituito dalle infinite rette parallele a una retta data e non da tre rette.] Altri utilizzano, senza averlo preliminarmente dimostrato, il parallelismo di certe rette. [Vogliamo precisare che il teorema di Talete, senza opportune precisazioni, non è in generale invertibile, mentre lo è il suo corollario applicato ai triangoli.] Altri forniscono una soluzione incompleta, oppure, dopo aver verificato con Cabri l’allineamento dei punti in esame, non ne forniscono la dimostrazione [ribadiamo ancora che Cabri non fornisce dimostrazioni geometriche, ma permette solo di fare congetture]. Per quanto riguarda l’ultimo quesito in una sola risposta è presente la dimostrazione per assurdo che se il triangolo non è rettangolo [ma scaleno], allora la proprietà non vale [ma nella risposta non viene preso in esame il caso particolare del triangolo isoscele sulla base AB], altri considerano il caso particolare del triangolo isoscele, ma poi forniscono un’affermazione contraddittoria con quanto dimostrato nel primo quesito affermando che la proprietà non è valida per i triangoli scaleni e dimenticandosi in tal modo che ogni triangolo rettangolo avente i due cateti non congruenti è un particolare triangolo scaleno.

Sono pervenute risposte dalle seguenti scuole:

Si allega QUI il documento PDF con le risposte
NOTA. Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre.

| Home Page Cabri | Torna a FLATlandia | Archivi |