FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Maggio 2007

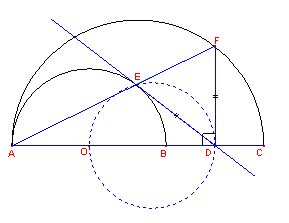
Presi tre punti allineati A, B, C (AB < AC) tracciare in uno stesso semipiano le semicirconferenze di diametro AB e AC.

  1. Detto D il punto medio di BC, costruire la retta per D tangente alla semicirconferenza di diametro AB. Sia E il punto di contatto.

  2. Detto F il punto in cui la retta AE incontra la semicirconferenza di diametro AC, determinare la natura dei triangoli EDF e ADF.

  3. Detto O il punto medio di AB, dedurre che OD^2 – DF^2 = OA^2.

E’ facoltativo studiare il luogo descritto da F al variare di C sulla retta AB

Giustificare la costruzione e motivare le risposte

     

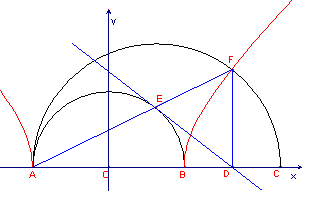
Equazione luogo: x2 – y2 = OA2,   y>0
 

Commento

Abbiamo ricevuto tre soluzioni dalle scuole:

Nel problema proposto, date due semicirconferenze tangenti internamente, si chiedeva di costruire la retta tangente alla minore da un punto assegnato e di individuare le caratteristiche di due triangoli opportunamente ottenuti all’interno della semicirconferenza maggiore. Si chiedeva inoltre di dimo-strare la relazione che intercorre fra i quadrati costruiti su tre segmenti della figura, assegnata in modo da portare poi alla scoperta di un luogo geometrico, il cui studio era richiesto come parte fa-coltativa.

Nella risoluzione proposta dalla classe 2M del LS “Aristosseno” non viene descritta inizialmente la costruzione della retta tangente richiesta.
Si sono comunque dimostrate in modo corretto e completo le successive due richieste; non viene ri-solta la parte facoltativa sul luogo geometrico.

La soluzione proposta della classe 2B ST del “Berenini” presenta la costruzione della retta tangente in modo corretto. Complete anche le parti b) e c), con dimostrazioni analoghe a quelle presentate dalla classe 2M del LS “Aristosseno”.
La risoluzione degli allievi del “Berenini” presenta anche la parte facoltativa, in modo quasi corret-to, in quanto vi si afferma che il luogo è un’iperbole equilatera, mentre il punto F descrive solo una parte dell’iperbole, quella costituita dai punti di ordinata positiva. Si fornisce l’equazione del luogo, ma non si studiano completamente le sue caratteristiche.

Apprezzabile la risoluzione prodotta dagli allievi della classe 3S della scuola media “C.A. Dalla Chiesa” sia per la costruzione della retta tangente sia per la dimostrazione delle caratteristiche dei due triangoli attraverso l’applicazione delle proprietà delle omotetie. Utilizzando il software Cabri hanno anche dedotto che il luogo geometrico descritto dal punto F è un “ramo di iperbole”.

Si allega QUI il documento PDF con le risposte corredate dalle nostre osservazioni in parentesi quadra.
Salutiamo tutti coloro che ci seguono in questa attività, in particolare i ragazzi (e gli insegnanti) più assidui.
 

Buone vacanze !

Giuliana BETTINI
Giuliano MAZZANTI
Franca NOE’
Valter ROSELLI
Luigi TOMASI

| Home Page Cabri | Torna a FLATlandia | Archivi |