 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Dicembre 2006
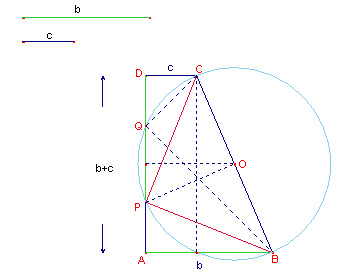
Sono dati due segmenti b e c (b>c).
Disegnare con essi un trapezio rettangolo ABCD di basi AB=b, DC=c e di altezza AD=b+c.
1) Verificare, e poi dimostrare, che la circonferenza di diametro CB incontra il lato AD in due punti che chiameremo P e Q (AP<AQ).
2) Determinare in funzione di b e c la lunghezza della corda PQ, le distanze di P e Q dai vertici A e D del trapezio e l’area del triangolo BPC.
Commento
Abbiamo ricevuto tre risposte dalle seguenti scuole:
Diamo il benvenuto agli studenti del LS “Righi”, contiamo
di vederli ancora impegnati nei quesiti che proporremo.
Nel problema dato si dovevano determinare le intersezioni fra un un lato di un
particolare trapezio rettangolo, costruito mediante due segmenti assegnati, e la
circonferenza avente come diametro il lato obliquo. Per non appesantire il
problema, abbiamo chiesto di dimostrare l’esistenza di tali punti dopo aver
verificato dalla figura che sono interni al lato AD (altezza del trapezio).
Si chiedeva inoltre la misura di alcuni elementi della figura in funzione di
quella dei segmenti dati.
Il trapezio assegnato presentava alcune caratteristiche che potevano essere
giustificate sia con considerazioni di geometria sintetica, sia ricorrendo al
calcolo algebrico.
Questo aspetto risulta anche nelle risposte ricevute; in esse i quesiti vengono
risolti con approcci diversi che commenteremo brevemente:
Si allega QUI il
documento PDF completo. Commenti ed eventuali correzioni, sono in
parentesi quadra nelle risposte. Con doppia parentesi quadra sono indicate le
parti omesse perché ritenute superflue.
| Home Page Cabri | Torna a FLATlandia | Archivi |