Flatlandia - Aprile 2007

FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Si racconta che Leonardo Pisano, detto Fibonacci, appena decenne, avendo smarrito la squadra e non volendo farlo scoprire al padre, avesse ideato un ingegnoso metodo per trovare il punto medio di un segmento con l’uso del solo compasso.
Ecco la costruzione:
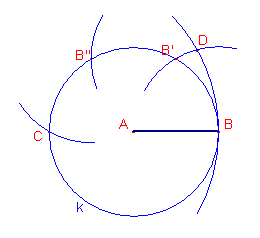
Dato un segmento AB si tracci la circonferenza k di centro A e raggio AB; con lo stesso raggio si traccino un arco di centro B che intersechi k in B’, poi un arco di centro B’ che intersechi k in B’’ e uno di centro B’’ che intersechi k in C.
Ora con centro C si tracci un arco di raggio CB e sia D il punto di intersezione con l’arco di centro B già tracciato.
[[…]]
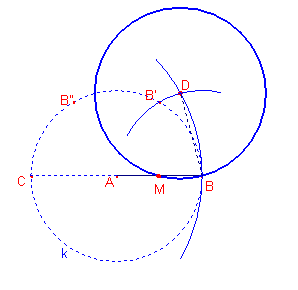
Lasciamo a voi l’ultimo passaggio che permette di individuare il punto medio M di AB

Non sappiamo se il piccolo Leonardo abbia giustificato la sua costruzione.
Volete provarci?

Abbiamo ricevuto tre risposte dalle scuole:

LS “Aristosseno”, Taranto (TA)
SM “C.A. Dalla Chiesa”, San Genesio ed Uniti (PV)
LS “A.Roiti”, Ferrara (FE)

Nel problema dato si descriveva la parte iniziale costruzione del punto medio di un segmento con l’uso del solo compasso, attribuita a Leonardo Pisano, detto Fibonacci, appena decenne, lasciando agli studenti il compito di trovare il passaggio conclusivo e di giustificare il risultato raggiunto.
La costruzione richiesta era abbastanza semplice, ma ci è piaciuta l’idea di presentare agli studenti, mediante un aneddoto, un altro aspetto di questo grande personaggio, noto soprattutto per la celebre successione che porta il suo nome e per la diffusione in Europa delle cifre arabe e della scrittura posizionale dei numeri.
Abbiamo inoltre facilitato la giustificazione suggerendo di dimostrare prima l’allineamento dei punti A, B, C, evitando agli studenti di lasciarsi ingannare dalla evidenza della figura.

Commentiamo ora brevemente ciascuna della risposte ricevute.

LS “Aristosseno”: gli studenti della classe 2M hanno completato la costruzione e fornito una dimostrazione succinta e completa, facendo ricorso alla similitudine. Abbiamo inserito nel testo due correzioni dove la loro esposizione ci è apparsa imprecisa.
SM “C.A. Dalla Chiesa”: una studentessa della classe 3S ha provato di giustificare la costruzione ricorrendo alla simmetria assiale, ma non ha saputo individuare un percorso corretto per giungere alla conclusione. Abbiamo comunque apprezzato il suo tentativo, presenteremo la prima parte della sua risposta e la figura della seconda parte, accompagnata da una breve descrizione, per illustrare la sua idea.
LS “A. Roiti”: Giacomo Bergami della classe 3H, che per la prima volta partecipa a FLATlandia, dopo aver completato la costruzione, l’ha giustificata in due modi. Attratto forse dalle tante circonferenze, ha proposto una dimostrazione analitica in cui abbiamo riscontrato alcune imprecisioni di procedimento e qualche passaggio superfluo. Ha fornito anche una dimostrazione di tipo sintetico, un po’ lunga nella esposizione, ma corretta. Presenteremo solo quest’ultima, anche se analoga a quella degli studenti dell’Aristosseno.

Si allega QUI il documento PDF completo. Commenti ed eventuali correzioni, sono in parentesi quadra nelle risposte. Con doppia parentesi quadra sono indicate le parti omesse perché ritenute superflue.