FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Gennaio 2006

Sia ABCD un quadrilatero convesso inscritto in una circonferenza. Le bisettrici degli angoli interni A, B, C, D incontrano la circonferenza rispettivamente in S, P, Q, R.

1) Di che natura è il quadrilatero SPQR?

2) Quale relazione intercorre fra le diagonali dei due quadrilateri?

3) Indicare una o più ipotesi su ABCD affinché SPQR sia un quadrato.

Motivare le risposte.

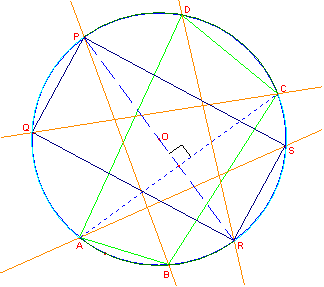Arco AR = arco RC Arco CP = arco PA Quindi Arco AR + arco PA = ½ crf. PR asse di AC

 

---

Commento

Sono giunte cinque risposte dalle seguenti scuole:

• SM “Paisiello”, IC “Buscaglia”, Cinisello Balsamo (MI)
• LS “Aristosseno”, Taranto (TA)
• ITI, LST “Berenini”, Fidenza (PR)
• ITCG “Ruffini” Imperia (IM)
• SM “C.A. Dalla Chiesa”, San Genesio (PV)

Diamo il benvenuto nel mondo di FLATlandia all’alunna della SM “Paisiello”, che, pur frequentando la seconda classe, si è cimentata con il problema di questo mese.

Abbiamo proposto ancora un problema sulla circonferenza, articolato in tre parti e avente come soggetto un qualunque quadrilatero inscritto.
Nella prima parte si doveva scoprire che le bisettrici dei suoi angoli interni incontrano la circonferenza in quattro punti, vertici di un rettangolo.
In tutte le risposte questa parte è stata risolta e motivata, con percorsi talvolta complessi o imprecisi nella esposizione.

Nella seconda si chiedeva di trovare il legame fra le diagonali dei due quadrilateri facilitando così la risposta al terzo quesito: quando quel rettangolo diventa un quadrato?
Non abbiamo chiesto esplicitamente di dimostrare che ogni diagonale del quadrilatero dato è perpendicolare ad una diagonale del rettangolo (e ne è anche l’asse), confidando nell’aiuto del software Cabri che quasi tutti i partecipanti usano. In proposito così scrivono le alunne della SM di San Genesio “Abbiamo verificato con Cabri che la relazione che intercorre tra le diagonali dei due quadrilateri è di perpendicolarità …”. Non hanno giustificato tale scoperta, ma a loro lo perdoniamo.
Abbiamo convenuto di presentare tre delle risposte ricevute, essendo le altre maggiormente incomplete nella risoluzione e/o nelle motivazioni.

• LS “Aristosseno”: è la sola risposta in cui si dimostra che le diagonali del quadrilatero dato sono anche gli assi di quelle del rettangolo.
• ITI, LST “Berenini”: in questa risposta, in cui manca la figura che illustra il punto 1), si fornisce l’esposizione più completa del terzo quesito.
• SM “C. A. Dalla Chiesa”: tutta la risposta, anche se carente nella seconda parte.

Come di consueto presentiamo tutti i commenti riuniti in questo unico file pdf  (richiede il diffuso Acrobat Reader)

| Home Page Cabri | Torna a FLATlandia | Archivi |