FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Aprile 2006

1. In un triangolo isoscele ABC tracciare una corda DE parallela alla base AB in modo da dividere il perimetro in due parti uguali.

2. Provate ad ottenere lo stesso risultato tracciando una corda FG parallela a uno dei due lati congruenti.

Descrivere e motivare le costruzioni.

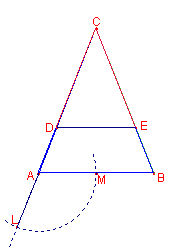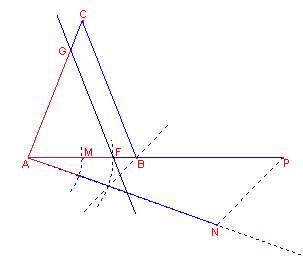LC semiperimetro D punto medio di LC	AN semiperimetro; BP=BC Retta per B parallela a NP

---

Commento

Abbiamo ricevuto sei risposte dalle seguenti scuole:

• LS “G.B. Scorza”, Cosenza (CS)
• SM “Paisiello”, Cinisello Balsamo (MI)
• ITCG “Ruffini”, Imperia (IM)
• SM “C.A. Dalla Chiesa”, San Genesio ed Uniti, (PV) – due risposte
• ITI “Galileo Ferraris”, San Giovanni La Punta (CT)

Nel problema proposto si chiedeva di dividere in due parti uguali il perimetro di un triangolo isoscele, prima tracciando una corda parallela alla base, poi parallela a uno dei due lati congruenti.
Si trattava quindi di procedere a una costruzione motivata o da una dimostrazione sintetica o da una verifica algebrica.
In quasi tutte le risposte gli studenti hanno interpretato correttamente il primo quesito, anche se con motivazioni non sempre esaurienti.
Il secondo quesito ha invece creato qualche difficoltà: c’è chi non lo ha risolto; c’è chi ha fatto ricorso alla risoluzione algebrica senza fornire la costruzione.
Pur essendo corrette, le risoluzioni mediante equazione individuano tramite una misura il punto da cui tracciare la parallela richiesta; si doveva comunque cercare un procedimento geometrico (riga e compasso) per determinare la posizione di tale punto.
L’unico studente che ha fornito una costruzione ben motivata ha “dimenticato” poi di trarre la dovuta conclusione.

Nelle figure che illustrano il testo del problema proponiamo la traccia di due possibili soluzioni alternative a quelle ricevute.

Abbiamo convenuto di presentare le risposte di :

• Gruppo classe 2A ITI “Galileo Ferraris”: solo la prima parte, in cui si fornisce una costruzione correttamente motivata. Una proposta analoga hanno inviato Elda Bistika, SM “C.A. Dalla Chiesa” e Paola Tonussi, SM “Paisiello”.
• Gruppo classe 2S SM “C.A. Dalla Chiesa”: hanno risolto solo il primo punto con una soluzione molto semplice, che presenta però una omissione nelle motivazioni.
• Alfonso Scarpino, 1G LS “G.B. Scorza”: ha individuato un procedimento di costruzione valido sia per la prima che per la seconda parte del problema. Presentiamo la seconda con una nostra nota a conclusione del suo percorso.

Si allega QUI il documento PDF con le risposte corredate dalle nostre osservazioni in parentesi quadra. Con la doppia parentesi quadra vengono indicate le parti omesse perché superflue o inopportune.

| Home Page Cabri | Torna a FLATlandia | Archivi |