 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Ottobre 2004
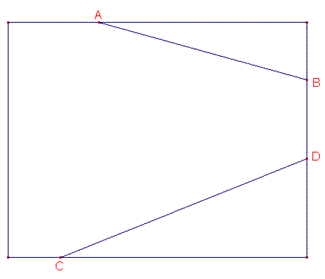
AB e CD sono porzioni di rette che si
incontrano fuori dal foglio qui rappresentato dal rettangolo.
Costruire la bisettrice degli angoli acuti formati dalle due rette mediante
costruzioni eseguite esclusivamente sul foglio assegnato.
Commento
Abbiamo ricevuto numerosi messaggi, ma non tutti leggibili
e qualcuno senza testo né allegato.
Per garantire la ricezione delle vostre risposte a ciascun componente del gruppo
di lavoro, e per facilitare la collocazione in rete delle soluzioni scelte,
proponiamo di NON scrivere il testo nei file delle figure MA di inviare allegati
formato Word contenenti testo e figura insieme.
Siamo riusciti a leggere tredici risposte provenienti dalle scuole:
Non abbiamo invece potuto esaminare quelle delle scuole
Nel problema avevamo proposto di costruire la bisettrice
di un angolo di cui non si vede il vertice, perché fuori dal foglio di lavoro.
Questo era rappresentato da un rettangolo in cui due segmenti dati erano
porzioni dei lati dell’angolo.
La costruzione doveva essere eseguita all’interno del rettangolo assegnato.
In tutte le risposte che abbiamo esaminato la bisettrice è stata individuata nel
modo richiesto, cioè con costruzioni interne alla figura data, ma solo in una ci
si è chiesti se e come il procedimento seguito rispettasse tale condizione (vedi
Giacomo Canevari, LS “Aselli”).
I punti presi in modo “qualunque” sui due segmenti assegnati da cui tracciare
poi rette perpendicolari o parallele, oppure bisettrici di angoli, dovevano
essere scelti in modo “opportuno” affinché le costruzioni successive
risultassero interne al rettangolo. Non si chiedeva in modo esplicito di
determinare le condizioni di esistenza della costruzione, ma sarebbe stato
corretto tener presente quella necessità nella scelta “arbitraria” di quei
punti.
Quando si propone una costruzione, si deve intendere una costruzione eseguibile
con riga e compasso anche se si fa ricorso allo strumento informatico. La
maggior parte ha individuato la bisettrice richiesta mediante due suoi punti
costruiti in modi diversi.
Presenteremo le risposte ritenute più significative per illustrare i diversi
percorsi seguiti per risolvere il quesito. Come al solito le risposte degli
studenti di scuola media inferiore vengono accolte anche se incomplete nelle
giustificazioni.
NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.
Soluzione proposta da:
Giacomo Canevari, classe 3C
Liceo Scientifico “G. Aselli” Cremona (CR)
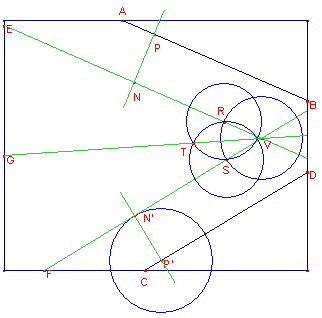
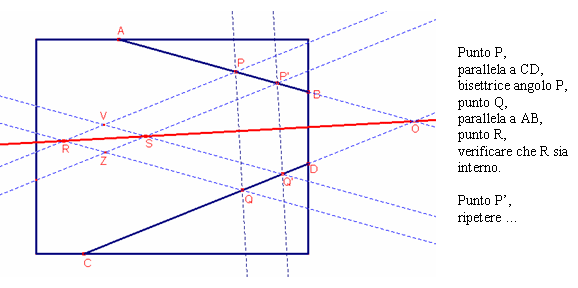
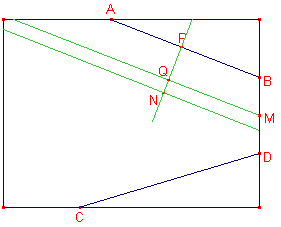
Presi a piacere un punto P su AB e uno P’ CD, tracciamo le perpendicolari ai segmenti passanti per questi. Chiamiamo poi N un punto qualunque della perpendicolare ad AB e disegniamo la parallela al segmento; quindi tracciamo la circonferenza di centro P’ e raggio congruente a PN, che interseca la perpendicolare a BC in punto N’, interno all’angolo determinato dalle rette AB e CD. Disegniamo quindi la parallela a CD per N’, che interseca la parallela ad AB in un punto V.
Tracciata una circonferenza qualsiasi di centro V,
troviamo sulle due rette NV e N’V rispettivamente i punti R ed S; l’intersezione
tra la circonferenza di centro R e raggio RS e quella di centro S e raggio pure
RS è il punto T.
I triangoli RTV e STV sono congruenti per il terzo criterio:
RV = VS per costruzione,
RT = TS per costruzione,
VT è in comune.
Dunque, gli angoli RVT e TVS sono congruenti fra loro; la retta TV è bisettrice
dell’angolo RVS.
Resta da dimostrare che essa è anche bisettrice dell’angolo determinato dalle
rette AB e CD.
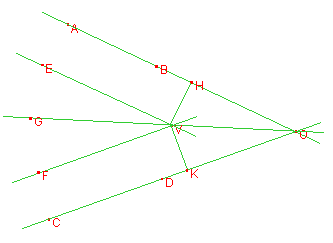
Si congiunga V con O.
Sappiamo che, per costruzione, EV è parallelo ad AB, mentre FV è parallelo a CD;
inoltre, indicati con H e K i piedi delle perpendicolari condotte da V
rispettivamente alla retta AB e alla retta CD, VH = VK. Ora, i triangoli OVH e
OVK sono congruenti tra loro per il quarto criterio, valido per i triangoli
rettangoli:
OP è in comune,
VH = VK,
VHO = VKO = 90°.
Quindi, gli angoli HOV e KOV sono congruenti e la retta OV è bisettrice
dell’angolo AOC. Tale retta è anche bisettrice di HVK, perché HVO = KVO;
inoltre,
EVO = EVH + HVO = KVO + 90° = KVO + KVF = FVO
da cui si ricava che la retta OV è bisettrice dell’angolo
EVF e che, quindi, le bisettrici degli angoli AOC e EVF coincidono tra loro. La
costruzione è pertanto giustificata.
N.B.: la scelta dei punti P e P’ non influisce sulla
costruzione.
Invece, dalla misura di NP dipende la posizione del punto V e va quindi scelto
un punto N tale per cui V cada interno al foglio. Si potrebbe, per esempio,
trovare il punto medio M di BD, tracciare la parallela ad AB per M, che
intersecherà la perpendicolare per P in un punto Q, e scegliere un punto N dalla
parte opposta a Q rispetto a P.
Soluzione proposta da:
Barbanera Mattia, classe 2E
Liceo Scientifico “G. Alessi”, Perugia (PG)
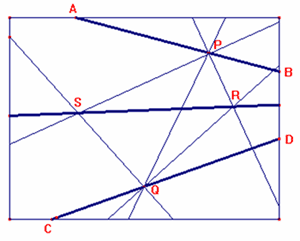
Il procedimento è abbastanza semplice: Sia P un punto
[[qualsiasi]] su AB e sia Q un punto [[qualsiasi]] su CD; si congiunga P con Q e
si traccino le bisettrici degli angoli APQ e CQP, che si incontreranno nel punto
S, e le bisettrici di BPQ e DQP, che si incontreranno nel punto R [R e S debbono
risultare interni al rettangolo e questo dipende dalla scelta di P e Q].
Si può dimostrare che la retta congiungente S e R è la bisettrice dell’angolo
acuto formato da AB e CD.
Infatti il punto R, appartenendo alla bisettrice dell’angolo QPB è equidistante
dai lati PB e PQ; ma R appartiene anche alla bisettrice dell’angolo DQP, quindi
è equidistante dai lati PQ e QD; quindi, per la proprietà transitiva della
congruenza, R è equidistante dai lati PB e QD, cioè dalle rette AB e CD: risulta
pertanto sulla bisettrice richiesta. Analogamente si dimostra che anche il punto
S appartiene alla bisettrice richiesta. Congiungendo dunque il punto R con il
punto S, il problema è risolto.
Soluzione proposta da:
Classe 2F - Istituto tecnico Agrario “G. Pastori” - Brescia (BS)

Traccio le bisettrici degli angoli CAB e DCA , trovo il
loro punto di intersezione M:
per definizione di bisettrice, M è equidistante sia dal lato AB che al lato AC,
perché punto della bisettrice dell'angolo CAB, ma M è anche equidistante dai
lati CD e AC, perché punto della bisettrice dell'angolo DCA.
Per la proprietà transitiva, M è equidistante sia da AB che da CD.
[Presi un punto E su AB e un punto F su CD], ripetiamo la
costruzione alla ricerca di un secondo punto:
Traccio le bisettrici degli angoli DFE e BEF, trovo il loro punto d'intersezione
N:
[N deve risultare interno al rettangolo e questo dipende dalla scelta di E e di
F]
N è equidistante sia dal lato EB che dal lato EF, perché punto della bisettrice
dell'angolo BEF,
ma N è anche equidistante dai lati FD e EF, perché punto della bisettrice
dell'angolo DFE.
Per la proprietà transitiva, N è equidistante sia da EB che da FD, quindi è
equidistante da AB e CD.
Poiché i punti M e N sono equidistanti dai segmenti AB e CD, sono punti appartenenti alla bisettrice dell'angolo avente per lati AB e CD. (l'angolo che si formerebbe col prolungare i due lati fuori dal foglio).
Soluzione proposta da
Thomas Neri e Mattia Rovelli
classe 3P Scuola Media “ C. A. Dalla Chiesa” - San Genesio ed Uniti (Pavia)
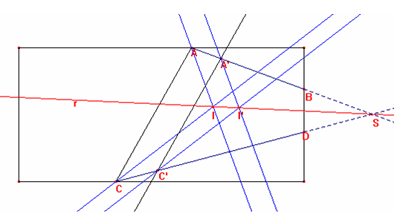
Uniamo A con C e consideriamo l'ipotetico
triangolo ASC (S punto di intersezione delle rette AB e CD).
Noi sappiamo che le bisettrici degli angoli interni di un triangolo si
incontrano in un unico punto.
Tracciamo le bisettrici degli angoli CAS e ACS; il punto di incontro è
l’incentro (I) del triangolo ASC.
Per l’incentro passerà anche la bisettrice dell’angolo ASC ma, dato che con solo
questo punto non possiamo tracciare la bisettrice dell’angolo ASC, tracciamo una
retta parallela al lato AC che interseca AB e CD rispettivamente nei punti A’ e
C’.
I triangoli A’C’S e ACS sono ugualmente disposti e simili, perché hanno gli
angoli interni rispettivamente uguali [perché corrispondenti], CAS=C’A’S ACS=A’C’S,
e l’angolo ASC in comune; quindi le bisettrici dell’angolo ASC e dell’angolo A’SC’
coincidono.
Tracciamo le bisettrici relative agli angoli C’A’S e A’C’S il loro punto di
incontro è l’incentro (I’) relativo al triangolo A’C’S. Da questo incentro
passerà anche la bisettrice dell’angolo A’SC’.
A questo punto [se I’ è interno al rettangolo] tracciamo una retta r passante
per i due incentri; così facendo troviamo la bisettrice dell’angolo ASC=A’SC’.
Soluzione proposta da:
Classe 3F - Scuola Media “G. B. Tiepolo” Milano (MI)

Per tracciare la bisettrice è sufficiente
individuare due punti.
Congiungendo A con C si ottiene un triangolo il cui vertice O è esterno al
foglio di lavoro.
Sapendo che le bisettrici di un triangolo si incontrano nell’incentro e sapendo
che sono sufficienti due bisettrici per poter trovare questo punto, tracciamo le
bisettrici degli angoli A e C.
Troviamo in questo modo il punto I; dal quale siamo sicuri passerà anche la
bisettrice dell’angolo O
Abbiamo così trovato il primo punto necessario per la costruzione della
bisettrice; per trovare il secondo punto tracciamo le perpendicolari ai lati AB
e CD passanti per il punto I, trovando i punti L e M. Il punto I è equidistante
dai due segmenti AB e CD, perciò IL=IM.
Fissiamo un punto sul segmento AB ad una certa distanza dal punto M, riportiamo
un punto anche sul segmento CD, mantenendo la stessa distanza con il punto L.
[[…]]
Chiamiamo i due punti S e T. SM=TL
Da questi due punti tracciamo le perpendicolari rispettivamente al segmento AB e
CD trovando in questo modo il secondo punto della bisettrice chiamato R.
[essendo RS=RT; affermazione che deve però essere dimostrata].
Avendo due punti [equidistanti dai lati] possiamo ora tracciare la bisettrice
all’angolo O, passante per i punti R ed I.
Soluzione proposta da:
alcuni alunni della classe 3C
Scuola Media “F. Besta” - Bologna
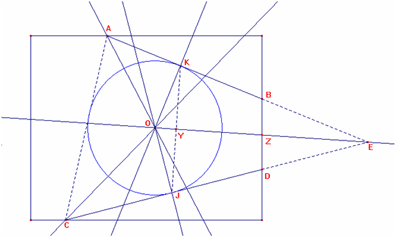
Costruiamo AC e poi le bisettrici degli angoli ACD e CAB. Il loro punto d'intersezione O rappresenta l'incentro del triangolo ACE (il punto E ottenuto prolungando i segmenti AB e CD). Il punto O è anche un punto delle bisettrici richieste dal testo.
Costruiamo da O i segmenti perpendicolari ad AB e CD che chiamiamo OK e OJ. Successivamente tracciamo la circonferenza di centro O inscritta nel triangolo di raggio OK.
Tracciamo il segmento KJ e individuiamo il triangolo isoscele KOJ. Infine tracciamo l'asse del segmento KJ. L'asse rappresenta anche le bisettrici degli angoli acuti formati dal prolungamento di AB e CD. [Conclusione corretta, ma affrettata; poteva essere motivata con maggior precisione]
| Home Page Cabri | Torna a FLATlandia | Archivi |