FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Novembre 2004

ll testo del problema:

1) Costruire un parallelogrammo noti i punti medi di tre lati.

2) Come debbono essere scelti i tre punti per ottenere un rettangolo, un rombo, un quadrato?

Motivare le risposte.

Figura proposta dalla Scuola Media di Vicoforte (CN)

Commento

Questa volta abbiamo ricevuto 24 risposte provenienti dalle scuole:

• LS “G. Aselli” Cremona – due risposte
• SM “F. Besta”, Bologna
• LS “L. da Vinci”, Bisceglie (BA) – tre risposte
• LC “Aristosseno”, Taranto
• LS “G. B. Scorza”, Cosenza
• ITI, LST “Cesaris”, Casalpusterlengo (LO)
• IIS “M. Curie”, Pergine, (TN)
• SM “C. A. Dalla Chiesa”, S. Genesio ed Uniti (PV)
• ITI, LST “F. Berenini”, Fidenza (PR) – tre risposte
• ITG “Ruffini”, Imperia
• LS “N. Copernico”, Bologna – due risposte
• ITI, LST “F. Alberghetti”, Imola (BO)
• SM “Marco Polo”, Rolo (RE)
• SM “G. B. Tiepolo”, Milano
• SM “Zanella”, Roveredo in Piano (PN)
• ITA “G. Pastori”, Brescia
• Scuola media di Gaiarine (TV)
• Scuola media di Vicoforte (CN)

Nel problema avevamo proposto di costruire un parallelogrammo essendo dati i punti medi di tre lati e si chiedeva poi quali ulteriori ipotesi si dovevano fare sui tre punti per ottenere i tre parallelogrammi particolari.
La costruzione era semplice e si poteva effettuare in vari modi: c’è chi ha trovato il risultato con pochi passaggi utilizzando le proprietà dei punti medi e del parallelismo; chi, volendo usare principalmente il compasso, ha fatto ricorso ad una lunga serie di circonferenze; chi, invece del compasso, ha considerato simmetrie centrali o assiali per trasportare punti e segmenti.

Ci siamo trovati in imbarazzo nella scelta delle risposte da proporre all’attenzione dei partecipanti.
La “evidenza” del risultato ha fatto sì che molte costruzioni, semplici e ben fatte, non siano poi state giustificate o lo siano state solo in parte. Non bastava trovare un parallelogrammo, ma si doveva anche dimostrare che avesse quei tre punti come punti medi dei lati.
Si doveva dare una completa giustificazione del caso generale, punto (1), e trarre poi rapide conclusioni nei casi particolari, punto (2).

Riteniamo opportuno fare anche le seguenti osservazioni:

• pochi hanno considerato tutte le possibili varianti una volta scelti i tre punti (si veda la figura presentata con il commento);
• qualcuno ha giustamente osservato che i tre punti scelti non dovevano essere allineati;
• qualcuno ha citato in modo improprio il teorema di Talete.

E’ vero che congiungendo i punti medi di due lati opposti di un parallelogrammo si ottiene un segmento parallelo agli altri due lati, ma il teorema di Talete non afferma questo: NON ESISTE in generale il “teorema inverso” (si vedano la figura e il commento del problema di Gennaio 2004).

Presentiamo in questa pagina:

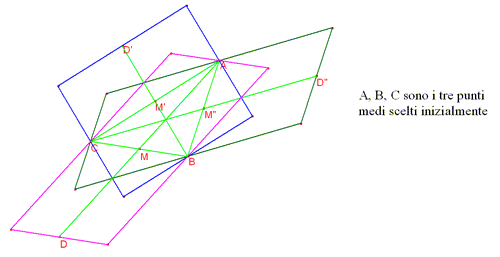
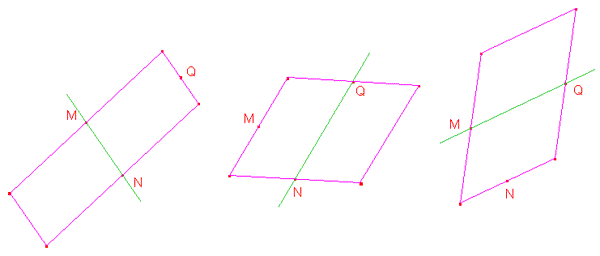
- la figura inviata dalla Scuola Media di Vicoforte (vedi sopra), in cui si mostrano i tre possibili risultati (una figura analoga hanno inviato un gruppo di studenti dell’ITI “Berenini”).

- le risposte provenienti dalle scuole:

• SM “Marco Polo”, prima e seconda parte, in cui si propongono costruzioni semplici e motivate.
• SM “C. A. Dalla Chiesa”, prima parte, in cui si fa prima una analisi della figura da ottenere per giustificare la successiva costruzione
• LS “G. Aselli”, quella di Giacomo Canevari, prima parte, in cui si propone una costruzione un po’ laboriosa e sostanzialmente giustificata.
• LS “L. da Vinci”, quella di Annalisa Todisco (ma simile alle altre), seconda parte, in cui si espongono i tre casi particolari in modo conciso facendo, come richiesto, le ipotesi sui tre punti scelti.

NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.

Soluzione proposta da:
classe 3°, Scuola Media “Marco Polo”, Rolo (RE)
Istituto Comprensivo “Italo Calvino”

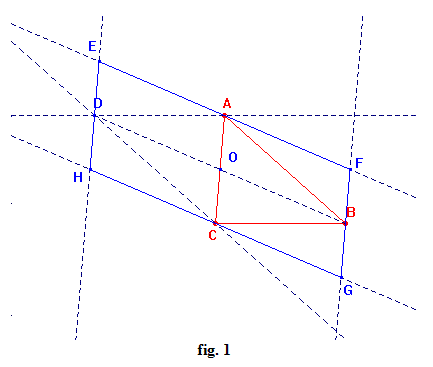
1)

Dati tre punti A, B, C suppongo che A e C siano i punti medi di due lati opposti del parallelogrammo, altrimenti vi sarebbero tre costruzioni possibili.

1. Mando da A la parallela a BC e da C la parallela ad AB e chiamo D il loro punto di intersezione.
2. Il quadrilatero ABCD è un parallelogrammo in quanto ha i lati opposti e paralleli per costruzione.
3. Mando per D e per B le parallele ad AC e per A e per C le parallele a DB ottenendo il parallelogrammo EFGH come in figura 1.
4. Se indico con O il centro del parallelogrammo ABCD [intersezione delle diagonali AC e BD] allora i quadrilateri AOBF e EDOA sono parallelogrammi avendo i lati opposti paralleli.
5. In particolare EA=DO e AF=OB perché lati opposti, ed essendo DO=OB perché in un parallelogrammo le diagonali si bisecano scambievolmente, allora EA=AF per cui A è il punto medio del lato EF. In modo analogo si dimostra che B è il punto medio di FG e che C è il punto medio di HG.

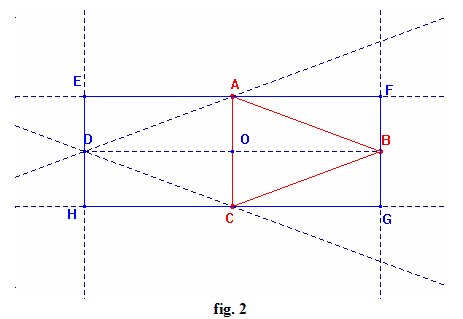
2)

Il parallelogrammo EFGH è rettangolo quando il triangolo ABC è isoscele di vertice B, infatti il parallelogrammo EFGH è rettangolo se e soltanto se AC e BD sono perpendicolari e quindi quando il parallelogrammo ABCD è un rombo (fig. 2).

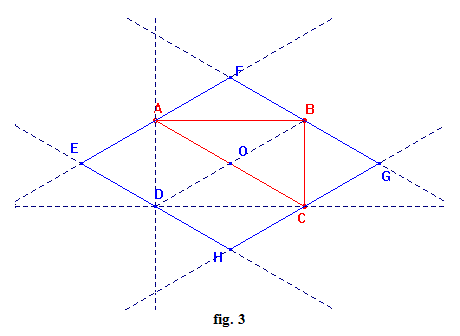
Il parallelogrammo EFGH è un rombo quando il triangolo ABC è rettangolo in B, infatti il parallelogrammo EFGH è un rombo se e soltanto se AC e BD sono uguali e quindi quando il parallelogrammo ABCD è un rettangolo (fig. 3).

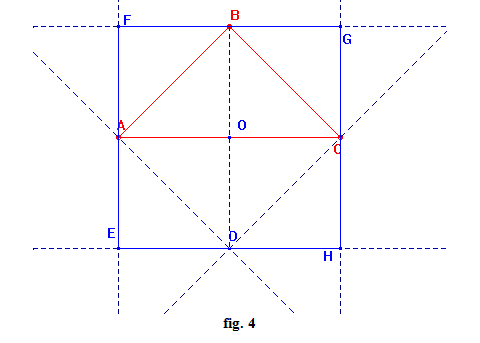
Il parallelogrammo EFGH è poi un quadrato quando il triangolo ABC è isoscele e rettangolo in B essendo un quadrato sia un rettangolo che un rombo (fig. 4).

Soluzione proposta da
Davide Cua, Virginia Lucaccini, Thomas Neri, Mattia Rovelli
classe 3P Scuola Media di San Genesio ed Uniti - (Pavia)

1)

In un parallelogramma il segmento che unisce i punti medi di due lati opposti risulta parallelo agli altri due lati [[per il teorema di Talete]] [vedi commento e la nota qui sotto], e i segmenti che uniscono i punti medi dei lati opposti si tagliano scambievolmente a metà, perché si formano quattro parallelogrammi uguali, simili a quello di partenza, aventi i lati di lunghezza la metà di quello di partenza.
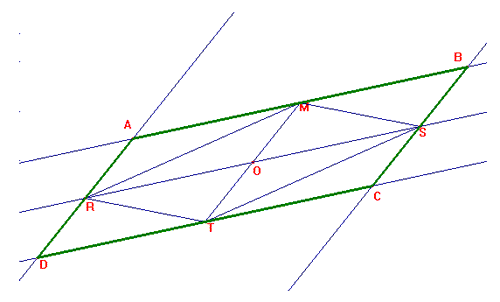
Presi nel piano i punti M, R,T, per trovare il punto medio del quarto lato del parallelogramma uniamo M con T e tracciamo la retta passante per R e per il punto medio O del segmento MT.
Con una simmetria centrale di centro O, troviamo il simmetrico di R che chiamiamo S.
In questo modo abbiamo trovato il punto medio del quarto lato.
Per le osservazioni fatte all’inizio è sufficiente, per costruire il parallelogramma richiesto, mandare le parallele ai segmenti MT ed RS passanti rispettivamente per i punti M, R, T, S. I punti di intersezione di queste quattro rette sono i vertici del parallelogramma ABCD che bisognava cercare.

[Nota: ADTM è un quadrilatero con due lati opposti, DT e AM, sia uguali che paralleli, quindi è un parallelogrammo e si ha AD parallelo a TM,…]

2) [[…]]

Soluzione proposta da:
Giacomo Canevari, classe 3C
Liceo Scientifico “G. Aselli” Cremona (CR)

1)

Costruzione

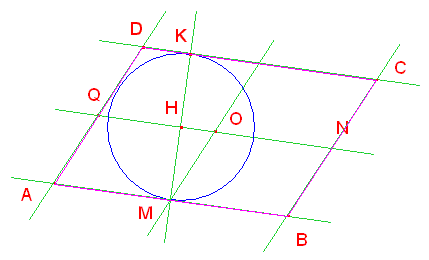
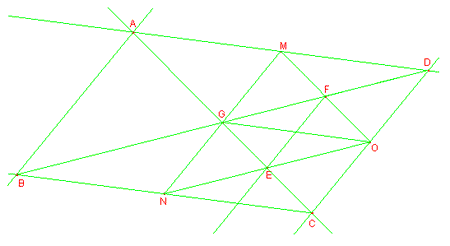
Chiamati M, N e Q i punti assegnati, tracciamo la retta passante per due di essi; consideriamo, per esempio, la retta NQ. Innalziamo la retta perpendicolare a NQ per il punto M, individuando il punto H; disegniamo la circonferenza di centro H e raggio HM, trovando il punto K, poi le rette parallele a NQ per i punti M e K. Trovato il punto medio O del segmento NQ, tracciamo la retta per O e M e le sue parallele per Q ed N; i punti di intersezione tra queste ultime e le parallele a NQ sono i vertici del parallelogrammo ABCD.

Dimostrazione

HP: ABCD parallelogrammo
AM = BM = CP = DP
AQ = DQ = BN = CN

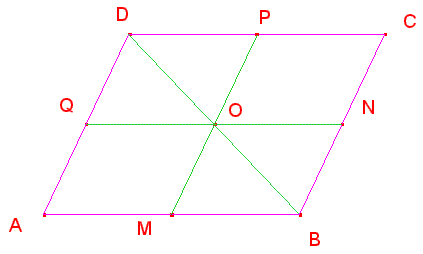
Poiché il parallelogrammo possiede un centro di simmetria O, che è il punto di intersezione delle diagonali [[…]], risulta che DO = BO, quindi che O è il punto medio di BD come Q lo è di AD. Perciò il segmento OQ è parallelo al lato AB, perché è il segmento congiungente i punti medi di due lati del triangolo ABD.
Ripetendo lo stesso ragionamento per la diagonale AC, otteniamo che MP e NQ sono paralleli ai lati e, dunque, dividono il quadrilatero ABCD in quattro parallelogrammi congruenti tra loro e simili ad ABCD secondo il rapporto k = ½, in quanto AM = ½ AB.
Da tutto ciò segue che O è il punto medio di NQ e che l’altezza dei quattro parallelogrammi minori è ½ di quella di ABCD: la costruzione è pertanto giustificata.

N.B.: non esistono limitazioni al problema, in quanto si basa su costruzioni (trasporto di distanze, punto medio, retta parallela) sempre possibili. La soluzione, tuttavia, non è unica: varia a seconda della retta considerata, quindi ne esistono tre per ogni terna di punti presa. Tutti i parallelogrammi ottenuti, però, sono equivalenti in quanto la loro area è il quadruplo dell’area del triangolo MNQ.

2) [[…]]

Soluzione proposta da:
Annalisa Todisco, classe 2D
Liceo Scientifico “L. da Vinci”, Risceglie (BA)

1.
[[…]]

2.
Se i punti medi M, N, O sono i vertici di un triangolo isoscele [[di base MN]] la mediana GO è anche altezza per cui i lati AD e DC che sono paralleli rispettivamente ai segmenti GO e MN risultano perpendicolari per cui il quadrilatero ABCD è un rettangolo.
Se i punti medi M, N, O sono i vertici di un triangolo rettangolo [[in O]], le diagonali del parallelogramma ABCD risultano perpendicolari, perché sono parallele ai cateti del triangolo MNO, quindi il quadrilatero ABCD è un rombo.
Se i punti medi M, N, O sono i vertici di un triangolo rettangolo isoscele il quadrilatero ABCD risulta sia un rettangolo che un rombo quindi è un quadrato.

| Home Page Cabri | Torna a FLATlandia | Archivi |