 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Marzo 2005
Il testo del problema:
1. Dato un segmento di lunghezza
a,
costruire il quadrato equivalente alla
superficie totale del cubo di spigolo
a.
2. Confrontare la diagonale del quadrato ottenuto con quella del cubo.
Commento
Abbiamo ricevuto otto risposte di cui una non è stata
accolta perché priva della costruzione richiesta.
Le risposte accolte provengono dalle scuole:
Nel problema assegnato si chiedeva di costruire un
quadrato equivalente alla superficie di un cubo e di confrontare le diagonali
delle due figure.
Le soluzioni pervenute sono corrette anche se non tutte esaurienti nelle
giustificazioni e/o precise nella esposizione. In esse si espongono tre diversi
percorsi di costruzione, di cui due dedotti dal calcolo della misura del lato
del quadrato richiesto e una basata sulla equivalenza di superfici.
Nelle risposte del LS “Scorza”, della SM “Dalla Chiesa” e
della SM “De Amicis”, si costruisce la “chiocciola” basata sul teorema di
Pitagora per ottenere i segmenti le cui misure, rispetto allo spigolo del cubo,
sono successivamente le radici quadrate dei numeri naturali 2, 3, …
Presenteremo in seguito la risposta della SM “Dalla Chiesa”. Le altre sono
visibili QUI e
QUI in formato PDF.
Nelle risposte del LS “Aristosseno”, della SM “Via Ribolle”
e della SM “Tiepolo” si ricorre ad un opportuno triangolo equilatero per
costruire il segmento che misura la radice quadrata di sei rispetto allo spigolo
del cubo.
Presenteremo in seguito la risposta del LS “Aristosseno”. Le altre sono visibili
QUI e
QUI in formato PDF.
Infine presenteremo la risposta della SM “Zanella”, in cui si utilizzano i teoremi di Euclide per trasformare un rettangolo, equivalente alla superficie del cubo, nel quadrato equiesteso.
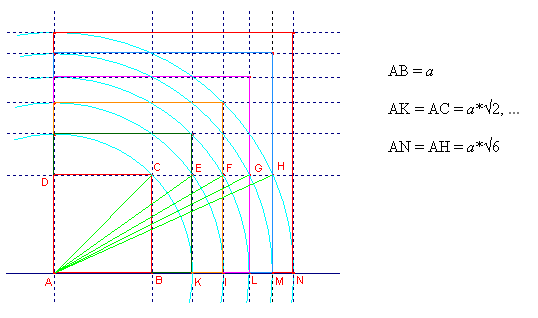
Nella nostra figura, allegata al testo del problema, presentiamo una ulteriore costruzione, basata sul teorema di Pitagora, che permette di ottenere una successione di quadrati di area doppia, tripla, …, rispetto al quadrato iniziale.
NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.
SOLUZIONI
Soluzione proposta da:
Davide Cua, Riccardo Fabbian, Virginia Lucaccini, Thomas Neri, Mattia Rovelli,
classe 3P, Scuola Media “C. A. Dalla Chiesa”
San Genesio ed Uniti (Pavia)
1) Se “a” è lo spigolo del
cubo, l’area di una faccia del cubo è a2 e quindi la
superficie totale del cubo è 6a2.
L’area del quadrato equiesteso alla superficie totale del cubo è 6a2
perciò il lato del quadrato è √(6a2 ) =√6√ (a2 )
=a√6
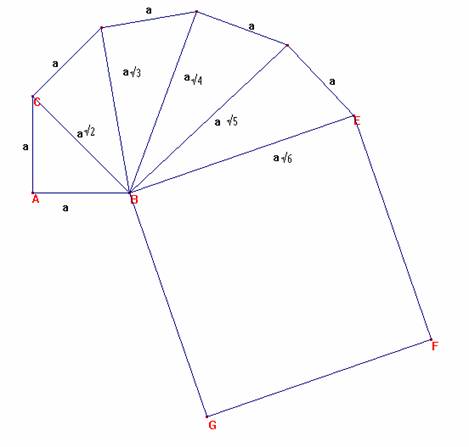
Per costruire il lato del quadrato abbiamo utilizzato la costruzione con
riga e compasso di √2, √3, √4 ecc che avevamo fatto in 2° media:
- Costruiamo
un triangolo rettangolo isoscele ABC con il cateto di misura “a”
-
L’ipotenusa del triangolo misura a√2
-
Mandiamo una retta perpendicolare all’ipotenusa CB passante per il punto C
- Su questa
retta perpendicolare riportiamo un segmento di misura “a”
- Uniamo
l’estremo del segmento con il punto B
- Otteniamo
un triangolo rettangolo la cui ipotenusa misura :
√(a2 + (a √2 ) 2
)=a√3
-
Ripetiamo la procedura fino ad ottenere un segmento la cui misura è
a√ 6
-
Costruiamo su questa ipotenusa il quadrato BEFG la cui area è 6 a2.
2) Diagonale del cubo è a√3
Diagonale del quadrato BEFG è a√6√2 = a√12 = 2a√3. Quindi la
diagonale del quadrato BEFG è il doppio della diagonale del cubo.
Soluzione proposta da:
classe I D - Liceo Scientifico “Aristosseno” Taranto (TA)
1.
Essendo la superficie di un cubo di spigolo a: S = 6*a^2,
il lato del quadrato avente area S sarà:
l = a*sqrt(6) = a*sqrt(3)*sqrt(2). Se allora costruiamo una circonferenza
di raggio a , e quindi il lato del triangolo equilatero in essa inscritto, la
cui misura è l’= a*sqrt(3), il lato l del quadrato richiesto sarà
la diagonale del quadrato che ha per lato l’.
E’ infatti l = l’*sqrt(2) .
La costruzione, effettuata con Cabri Géomètre, è nella seguente figura :
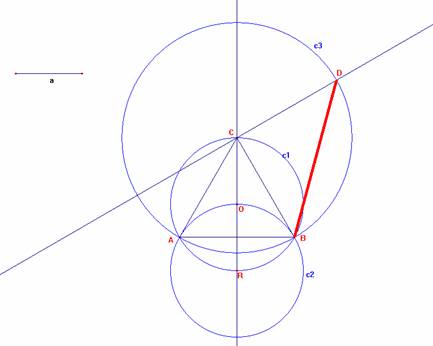
Precisamente: fissato un segmento di misura a, con
lo strumento Compasso del Cabri Géomètre , tracciamo una circonferenza c1 di
raggio a. Tracciato poi un diametro qualunque e detto R uno dei suoi
punti in comune con c1, la circonferenza c2 avente il centro in R e raggio a
individua su c1 gli estremi A e B del lato del triangolo equilatero inscritto in
essa [C, estremo del diametro CR, è il terzo vertice del triangolo].
A partire dal lato CB del triangolo equilatero così ottenuto, costruiamo la
diagonale del quadrato di lato CB tracciando la retta perpendicolare a CB nel
punto C e quindi la circonferenza c3 di centro C e raggio CB.
Il segmento BD è il lato del quadrato richiesto dal problema.
2.
Essendo BD = a*sqrt(6), la diagonale del quadrato di
lato BD sarà d = BD *srqt(2)=2*a*sqrt(3)
mentre la diagonale del cubo di spigolo a è data da: d’ = sqrt(3*a^2)
= a*sqrt(3)
Se ne deduce allora che: d = 2*d’ , cioè la diagonale del quadrato
che abbiamo costruito è doppia di quella del cubo.
Soluzione proposta da:
classe 3A (gruppo di approfondimento)
Scuola Media “Zanella”, Roveredo in Piano (PN)
 |
|
| 2° Teor. Euclide | 1° Teor. Euclide |
1)
- Con i quadrati delle sei facce del cubo
costruiamo un rettangolo (le dimensioni, [rispetto allo spigolo del cubo]
possono essere: 1 e 6 o 2 e 3) che in tal modo risulta equivalente all’area
totale del cubo.
- Nelle
rappresentazioni geometriche dei Teoremi di Euclide il rettangolo può avere per
dimensioni:
- le
proiezioni dei cateti sull’ipotenusa (equivalente al quadrato costruito
sull’altezza rispetto all’ipotenusa, per il 2° teorema );
-
l’ipotenusa e la proiezione di un cateto sull’ipotenusa (equivalente al quadrato
sul cateto considerato, per il 1° teorema).
-
Descriviamo la costruzione che utilizza il 2° Teorema di Euclide.
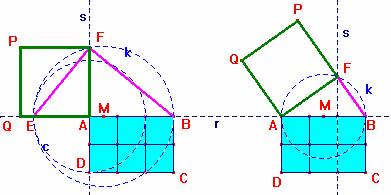
1. Rettangolo ABCD; rette per AB (r) e per AD (s);
2. Circonferenza c di centro A per D e sua intersezione E con la retta r (EB è l’ipotenusa del triangolo rettangolo che stiamo disegnando);
3. Punto medio M tra E e B; circonferenza k di centro M per B e sua intersezione F con la retta s (FA è l’altezza del triangolo rettangolo EBF rispetto l’ipotenusa, rettangolo perché inscritto in una semicirconferenza per costruzione). 4. Costruiamo il quadrato AFPQ che risulterà equivalente al rettangolo ABCD (per il 2° Teorema di Euclide).
2)
Diagonale del cubo: a√3 ;
Lato del quadrato: √(6a2);
Diagonale del quadrato: √(6a2)*√2 = √(12a2) = a √12.
Il rapporto tra la diagonale del cubo e la diagonale del quadrato risulta: √(1/4) = 1/2.
| Home Page Cabri | Torna a FLATlandia | Archivi |