FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Febbraio 2005

Il testo del problema:

Dato un quadrato ABCD siano P e Q due punti qualunque presi rispettivamente sui lati BC e CD.
Congiungendo P e Q con gli estremi dei lati ad essi opposti, si ottiene il quadrilatero ATRS, come si vede nella figura allegata.

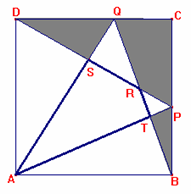
a) Dimostrare che tale quadrilatero è equivalente alla parte di figura colorata in grigio.
b) Se P e Q sono i punti medi dei lati BC e CD, quali caratteristiche assume il quadrilatero ATRS?
c) Calcolare l’area di ATRS del caso b) considerando 1 (uno) la misura del lato del quadrato.

Commento

Ci sono pervenute sette risposte da sei scuole equamente divise fra secondaria inferiore e secondaria superiore:

• LS “G. B. Scorza”, Cosenza (CS)
• LS “Aristosseno” Taranto (TA)
• SM “C. A. Dalla Chiesa”, S. Genesio ed Uniti (PV) – due risposte
• SM “Zanella”, Roveredo in Piano (PN)
• ITI, LST “F. Berenini”, Fidenza (PR)
• SM “G. B. Tiepolo”, Milano (MI)

Il problema proposto in questo mese, per evitare lunghe descrizioni, era accompagnato dalla figura. A questa faremo ora riferimento per descriverne gli aspetti essenziali: presi due punti, P e Q, su due lati consecutivi di un quadrato ABCD, congiungendoli con gli estremi dei lati a loro opposti, si ottiene il quadrilatero ATRS.

• Primo quesito: dimostrare l’equivalenza fra il quadrilatero ATRS e la parte di quadrato colorata in grigio. Le risposte a questo quesito sono, tranne una, corrette e completamente giustificate.
   
• Secondo quesito: osservare, motivandole, le caratteristiche del quadrilatero ATRS nel caso particolare che i punti P e Q siano i punti medi dei lati del quadrato.
  La figura assume una “evidente” simmetria rispetto alla diagonale AC del quadrato e probabilmente per questo motivo in nessuna delle risposte questa parte è stata risolta in modo esauriente.
  Si fa notare che i vertici T, R, S non sono assegnati, ma risultano dalle intersezioni delle congiungenti prima dette. Si doveva quindi valutare il ruolo assunto da questi punti nel caso particolare proposto: S e T diventano vertici di angoli retti; R si viene a trovare sulla diagonale del quadrato e la divide in due parti una doppia dell’altra (infatti R diviene baricentro del triangolo DBC come hanno osservato due studenti dell’ITI “Berenini”).
  L’appartenenza di un punto a un segmento, come pure l’allineamento di tre punti, è una questione “sottile” che spesso sfugge agli studenti, tratti in inganno dalla evidenza della figura.
   
• Terzo quesito: si chiedeva il calcolo dell’area di ATRS, che nel caso particolare diventa un deltoide. Non tutti hanno risposto a questa parte: chi non ha “visto” gli angoli retti in S e T non era in grado di risolverla.

Altre osservazioni:

• non sempre, dove si fa ricorso alle isometrie, le proprietà osservate vengono giustificate in modo esplicito; ribadiamo che prima di affermare che triangoli con un vertice in R sono simmetrici rispetto all’asse AC, si doveva far notare che i segmenti simmetrici BQ e DP si incontrano sull’asse AC;
• per chi ha utilizzato i criteri di congruenza dei triangoli, dimostrare l’allineamento di R con A e C non è immediato, si possono sfruttare le proprietà del triangolo isoscele BDC in cui BQ e DP sono mediane;
• nei calcoli è preferibile esprimere i risultati in forma esatta, ricorrendo agli opportuni simboli (frazioni, radici quadrate, …);
• non si devono confondere i teoremi di Euclide con quello di Talete.

Presentiamo parti delle risposte di seguito elencate, corredate da ulteriori nostri commenti.
Quelle che contengono caratteri speciali sono proposte in formato PDF.

• SM “C. A. Dalla Chiesa”, classe 2P, prima parte, in cui si è scelta una esposizione discorsiva, ma esauriente.
• SM “C. A. Dalla Chiesa”, classe 3P, seconda e terza parte in cui si ricorre alla congruenza dei triangoli e alla similitudine (con figura presa a prestito dalla classe 2P perché mancante).
• SM “Zanella”, seconda e terza parte; nella seconda si utilizzano le isometrie e si dimostra il ruolo assunto dal punto R.
• LS “Aristosseno”, tutta; la seconda parte presenta alcune carenze nelle giustificazioni, ma in essa vengono individuate tutte le caratteristiche della figura.

NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.

Soluzione proposta da
Elda Bistika, Erika Dargenio, Monica Maida
Classe 2P, Scuola Media “C.A. Dalla Chiesa” di San Genesio ed Uniti (PV)

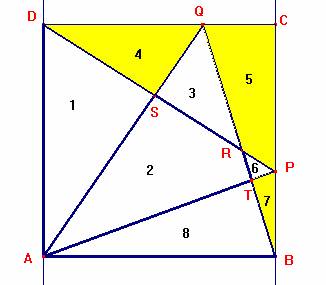
a)

Il triangolo AQB(formato dalle figure 3,2,8) è equiesteso al triangolo DPA (formato dalle figure 1,2,6) perché hanno la stessa base AD=AB e la stessa altezza : infatti la distanza del punto P dal lato DA è uguale alla distanza del punto Q dal lato AB, che è uguale al lato del quadrato.
Inoltre ognuno di questi  triangoli è equiesteso a metà del quadrato in quanto le dimensioni utilizzate nel calcolo dell’ area del triangolo (l*l/2) sono uguali al lato del quadrato (l*l)
Abbiamo visto che i triangoli AQB e DAP hanno in comune la figura indicata con il numero 2, e poiché i due triangoli sono equiestesi vuol dire che la somma delle aree delle figure indicate con 8 e 3 è uguale alla somma delle aree delle figure indicate con 1 e 6 (3+2+8= 1+2+6 per cui 3+8=1+6)
Se il triangolo APD è equiesteso a metà quadrato anche la rimanente superficie (che chiameremo “rimanente”) cioè la somma delle figure 4,3,5,7,8 è equiestesa a metà quadrato.
Se togliamo dal triangolo APD le figure 1+6 e dal “rimanente” le figure 3+8 equiestese a 1+6 otteniamo che la figura 2 è equiestesa alla somma delle figure 4+5+7. Quindi il quadrilatero ASTR è equiesteso alla parte di figura colorata in grigio per differenza di parti equiestese.

 b) [[…]]         

 c) [non risolto]

Soluzione proposta da:
Davide Cua, Riccardo Fabbian, Mattia Rovelli
classe 3P, S.M.S. di San Genesio ed Uniti (PV)

a) [[…]]

b)

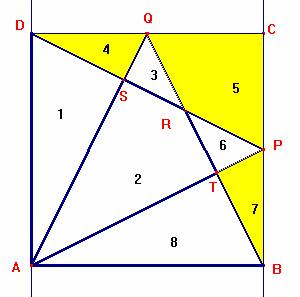
Nel caso in cui i punti P e Q sono punti medi dei lati BC e CD consideriamo i triangoli ADQ, BQC e ABP sono uguali perché hanno i cateti di uguale misura: AD=AB=BC e DQ=BP=QC per costruzione. Indichiamo gli angoli DAQ = PAB=QBC= alfa, allora gli angoli DQA=APB= BQC= (90°-alfa). Consideriamo il triangolo ATB avente l’angolo TAB uguale ad alfa, l’angolo ABT è (90°-alfa), quindi BTP=90°. Si dimostra nello stesso modo che DSA=90°. I triangoli ADS e ABT sono triangoli rettangoli congruenti perché hanno rispettivamente uguale un lato AD=AB e gli angoli uguali pertanto AS=AT. I triangoli ASR e ATR sono triangoli rettangoli congruenti avendo AS=AT e gli angoli SAR=RAT=(45° -alfa) [questa affermazione è vera solo se R appartiene alla diagonale AC, vedi commento], quindi anche SR=RT.
Il quadrilatero ASRT è un deltoide perché ha due coppie di lati consecutivi uguali.

c) I triangoli ATQ e SQR sono triangoli rettangoli (ATQ=QSR=90°) ed inoltre hanno l’angolo AQT in comune, per cui si deduce che gli angoli QAT=QRS perché complementari di angoli uguali e quindi i triangoli sono simili.

AQ = sqrt(AD2+DQ2) = (sqrt (5))/2
DS = (AD*DQ)/AQ = (sqrt (5))/5
SQ = sqrt (DQ2-DS2) = (sqrt (5))/10
AS = AQ-SQ = 2(sqrt (5))/5
QT = sqrt (AQ2-AT2) = 3(sqrt (5))/10
SR/AT = SQ/QT
SR = (AT*SQ)/QT = 2(sqrt (5))/15
Area (ASRT) = AS*SR = 4/15 essendo l’area del quadrato ABCD = 1

Soluzione presentata da
Classe 3A, Scuola Media “ZANELLA”
ROVEREDO IN PIANO (PN)

a) [[…]]
b)

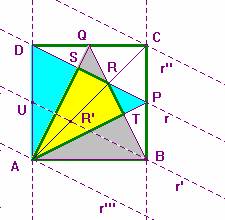
* I lati corrispondenti dei triangoli ABQ e APD sono perpendicolari, perché il triangolo ABQ si ottiene con una rotazione di 90° del triangolo APD attorno al punto medio della diagonale AC del quadrato. Consegue [poiché AP va in BQ e PD in QA] che i triangoli ATR e ASR sono rettangoli rispettivamente in T e S.
(I triangoli ABQ e APD sono simmetrici rispetto la diagonale AC  [quindi i lati corrispondenti BQ e PD si incontrano su AC])

*   I triangoli ABP e AQD sono rettangoli e tra loro congruenti per costruzione; i segmenti BT e DS sono  altezze rispetto l’ipotenusa dei rispettivi triangoli; AT e AS sono le proiezioni del cateto maggiore sull’ipotenusa (tra loro congruenti).

- I triangoli rettangoli ATR e ARS sono congruenti perché AT e AS congruenti per quanto detto sopra e AR è lato in comune. 

- Il segmento AR è 2/3 della diagonale del quadrato per quanto segue.           

*   Retta r per PD; retta r’ parallela ad r per B, sua intersezione U con il lato AD, sua intersezione R’ con AC; retta r’’ parallela ad r per C; retta r’’’ parallela ad r per B. Se P è punto medio del lato BC anche R è punto medio del segmento CR’ per il teorema di Talete; se BP è metà lato, anche DU lo è per lo stesso teorema, consegue che anche R’ è punto medio del segmento RA. I punti R ed R’ dividono la diagonale AC in tre parti uguali.

c)

AP = (sqrt5)/2 (ipotenusa del triangolo rettangolo ABP, teorema di Pitagora)
TB = 1/sqrt5 (cateto*cateto/ipotenusa; 1*1/2/sqrt(5/2); triangolo ABP)
AT = 2/sqrt5 (cateto maggiore del triangolo ABT; teorema di Pitagora)
AR = 2/3*sqrt2 (2/3 diagonale del quadrato di lato 1)
RT = 2/sqrt(45) (cateto minore del triangolo ATR; teorema di Pitagora)
Area del poligono ATRS = 2*(AT*RT )/2 = (2/sqrt5)*(2/sqrt(45)) = 4/15 (dell’area del quadrato)   

Soluzione proposta da
Notaristefano Preethi, classe I G
Liceo “Aristosseno”, Taranto

Vista la presenza di simboli graficamente complessi questa soluzione è disponibile in formato PDF Acrobat. Selezionare QUI per scaricarla.

| Home Page Cabri | Torna a FLATlandia | Archivi |