FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Aprile 2005

Il testo del problema:

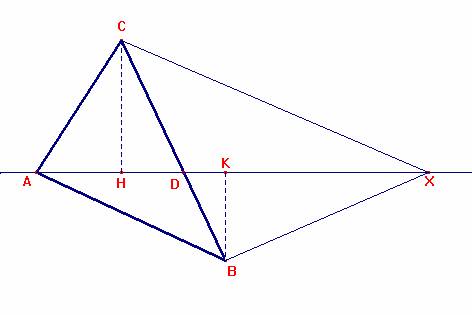
Dato un qualsiasi triangolo ABC ed un punto X sullo stesso piano, sia D il punto in cui la retta AX incontra la retta BC.

1. Dimostrare che il rapporto fra l’area del triangolo AXC e quella del triangolo AXB è uguale al rapporto dei segmenti DC e DB.

2. Esiste sempre tale rapporto?

3. Quali sono le posizioni del punto X per cui i triangoli suddetti risultano equivalenti?

Motivare le risposte.

Figura proposta da:
Mercedes Scarpino
Liceo Scientifico “G. B. Scorza”
Cosenza (CS)

Figura proposta da:

Fabbian Riccardo, Thomas Neri, Mattia Rovelli
3° P, S.M. San Genesio ed Uniti (PV)

Commento

Abbiamo ricevuto 9 risposte provenienti dalle scuole:

• LC “Aristosseno”, Taranto (TA)
• LS “G. B. Scorza”, Cosenza (CS)
• SM “C. A. Dalla Chiesa”, S. Genesio ed Uniti (PV)
• ITIS “F. Berenini”, Fidenza (PR)
• LS Istituto “B. Russell”, Roma (RM)
• SM “De Amicis”, Busto Arsizio (VA)
• SM “G. B. Tiepolo”, Milano (MI)
• SM “Zanella”, Roveredo in Piano (PN)
• LS "Galeazzo Alessi”, Perugia (PU)

Un’ulteriore risposta ci è giunta del LS “G. Aselli” di Cremona, che non possiamo includere nelle proposte da commentare perché realizzata da un alunno della classe terza; ci fa però piacere osservare che l’interesse per la geometria, e per FLATlandia, non si esaurisce nel biennio.

Nel problema di questo mese erano stati assegnati un triangolo ABC e un punto X nello stesso piano. Si doveva tracciare la retta congiungente il vertice A con il punto X, e considerare l’intersezione D di questa con la retta passante per gli altri due vertici del triangolo.
Il primo quesito chiedeva di dimostrare l’uguaglianza del rapporto fra le aree di due particolari triangoli e di due segmenti al variare della posizione di X nel piano.
Il secondo e il terzo chiedevano rispettivamente di verificare se tale rapporto esiste sempre e di considerare un caso particolare.

Tutte le risposte pervenute sono sostanzialmente corrette anche se non tutte sono complete e in alcuni casi contengono delle imprecisioni.
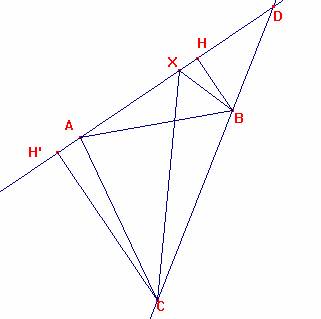
Modificando la posizione del punto X si ottenevano due differenti configurazioni: nella maggior parte delle risposte è stata dimostrata l’uguaglianza del rapporto soltanto in uno dei due casi; chi ha considerato correttamente i due casi non ha però fatto la giusta distinzione rispetto al punto X (si vedano le figure proposte prima del commento e di seguito le due diverse dimostrazioni dell’ ITIS “F. Berenini” di Fidenza e del Liceo “B. Russell” di Roma con le nostre correzioni). Solo nella risposta della scuola Media di Roveredo in Piano (visibile dopo il commento) è stata data un’unica dimostrazione dell’uguaglianza valida per tutte le posizioni del punto X in cui i rapporti considerati esistono.
Anche per il secondo e il terzo quesito solo una risposta proveniente dall’ITIS “Berenini” di Fidenza (visibile dopo il commento) è risultata completa avendo considerato tutti i casi possibili.

Per concludere riteniamo opportuno fare anche le seguenti osservazioni:

• il rapporto fra due grandezze non esiste quando il denominatore è nullo; se è soltanto il numeratore ad essere uguale a zero, allora il rapporto esiste e sarà anch’esso zero.
• qualcuno ha citato in modo improprio l’omotetia quando invece era più opportuno considerare la similitudine;
• Il problema risulta indeterminato nel caso in cui il punto X coincida con il vertice A del triangolo, poiché in questo caso la retta AX non è univocamente determinata.

Presentiamo le risposte di seguito elencate:

• SM “Zanella”, Roveredo in Piano (PN)- prima parte
• LS Istituto “B. Russell”, Roma- prima parte
• ITIS “F. Berenini”, Fidenza (PR)- risposta completa
  

NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.

SOLUZIONI

Soluzione proposta da:

Guendalina Antoniazzi e Stefania Basso Moro

classe 3°A, Scuola Media di Roveredo in Piano (PN)

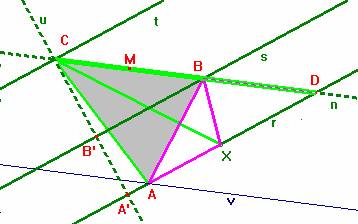
Triangolo ABC; Punto X; Retta n per C e B; Retta r per A e X; Punto D, intersezione di n ed r; Triangoli AXB e AXC.

1.

* Retta u perpendicolare alla retta r e passante per C; retta s parallela ad r per B; intersezione di u con r e con s: A', B'. [la retta s è perpendicolare alla u perché parallela a una sua perpendicolare]
Tracciamo le altezze CA' e B'A' dei triangoli AXC e AXB rispetto al lato AX in comune.
Le aree dei triangoli AXC e AXB avendo il lato AX in comune sono proporzionali alle relative altezze A'C e A'B' [A’B’ è altezza del triangolo AXB relativa ad AX perché r ed s sono parallele]
* Consideriamo il fascio di retta parallele r, s, t (per C) e le due rette u ed n. Per il Teorema di Talete i segmenti CA’ e B’A’ (sulla retta u) sono proporzionali ai segmenti CD e BD (sulla retta n), quindi per la proprietà transitiva anche le Aree dei triangoli AXC e AXB lo sono nei confronti di CD e BD. 

2. [[...]]

3. [[...]]

Soluzione proposta da:
Leonardo del Vecchio
2^a D, Istituto “B. Russell”, Roma

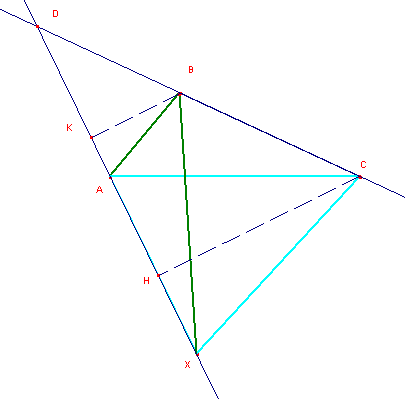
PUNTO 1:

Si disegnino le altezze BK e CH relative alla base AX.

I triangoli DKB e CHD sono simili perché:

BKD=DHK angoli retti per costruzione

KBD=HCD perché angoli corrispondenti formati dalle rette parallele BK e CH tagliate dalla trasversale BC [le rette BK e CH sono parallele perché perpendicolari alla stessa retta AX]

KDB=HDC [angolo in comune]

I triangoli ABX e ACX hanno la base AX in comune e come altezze (relative ad AX) hanno rispettivamente BK e CH, quindi il rapporto tra le aree sarà uguale al rapporto tra le altezze, cioè: A(ACX)/A(ABX)=CH/BK ma, poiché i triangoli DKB e CHD sono simili (come prima dimostrato) hanno i lati in proporzione, in particolare: CH/BK=CD/BD, quindi, si ha che A(ACX)/A(ABX)=CD/BD.

PUNTO 2:

[[...]]

PUNTO 3:

[[...]]

Soluzione proposta da:
2^a B, ITIS “Berenini”, Fidenza

1.      Se X appartiene all’angolo convesso individuato dalle semirette AC e AB (figura 1) [La configurazione della figura 1 si presenta anche quando X è interno all’angolo opposto al vertice dell’angolo convesso CAB, infatti anche in questo secondo caso il punto D è interno al segmento CB]

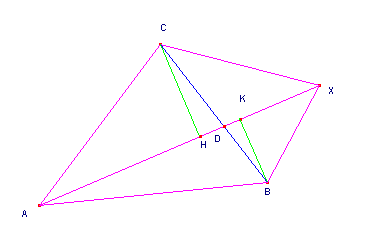
fig.1

o se X non vi appartiene [non appartiene ai due precedenti casi] (figure 2 e 3), i triangoli CDH e BDK sono comunque simili perché hanno i tre angoli rispettivamente congruenti (l’angolo BKD = CHD perché retti; l’angolo CDH = BDK perché opposti al vertice; l’angolo DBK = DCH perché alterni interni [considerazioni valide solo nel caso della figura 1; nel caso della figura 2 e 3: l’angolo BKD = CHD perché retti; l’angolo CDH = BDK perché in comune; l’angolo DBK = DCH perché corrispondenti]).

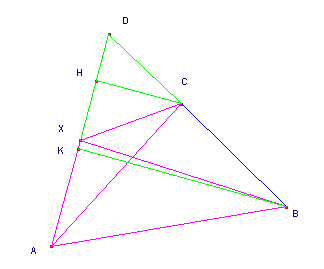fig.2 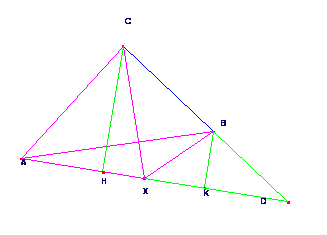fig.3

Quindi esiste la proporzione: CH / BK = CD / BD.
Poiché l’area del triangolo AXC è data (AX * CH)/2 e del triangolo AXB è (AX*BK)/2,   

si ha:

Area AXC/Area AXB=[(AX*CH)/2]/[(AX*BK)/2]=CH/BK=CD/BD  c.v.d.  

2.  Tale rapporto non esiste se BD=0 quindi D coincide con B, ciò succede se X appartiene alla  retta AB (figura 4).   

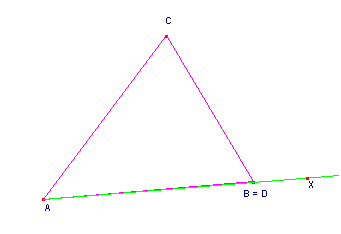fig.4

Inoltre se X sta sulla retta per A parallela a BC, D non esiste (figura 5).

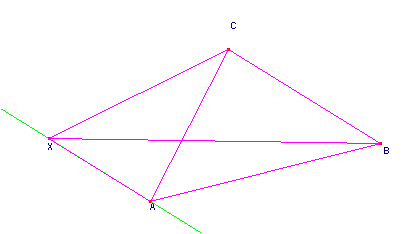fig.5

3.  I triangoli AXB e AXC sono equivalenti se hanno stessa area, quindi se il rapporto delle loro  aree è 1. Per quanto visto al punto 1 in tal caso, anche il rapporto CD/BD vale 1 e ciò si ha se CD=BD.

Quindi i triangoli sono equivalenti se CD=BD cioè se D è punto medio di CB; ciò accade se X sta sulla retta per A e per il punto medio di CB (figura 6).

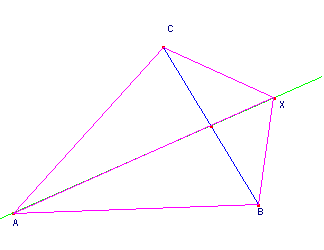 fig.6 

     Inoltre i triangoli sono equivalenti anche se X sta su qualsiasi punto sulla retta parallela al lato BC e passante per A (questo è lo stesso esempio di figura 5): dato che AX è un lato sia di AXB che di AXC e le sue altezze CH e BK sono congruenti (perché distanze tra due rette parallele) i triangoli sono equivalenti (figura 7).

fig.7

| Home Page Cabri | Torna a FLATlandia | Archivi |