 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Ottobre 2003
Il testo del problema:
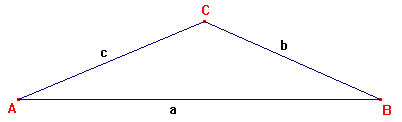
Sia dato un triangolo ABC.
a) Come deve essere fissato un segmento PQ affinché esista un triangolo PQR avente lo stesso perimetro di ABC?
b) Qualora un triangolo PQR del punto a) esista, descriverne almeno un metodo di costruzione.
Motivare le risposte
COMMENTO
 |
|
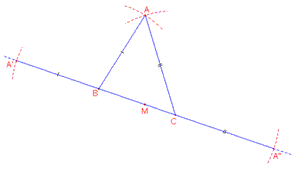
| Figura 1 | |
 |
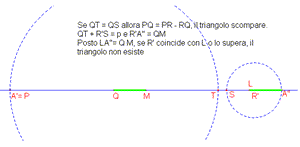 |
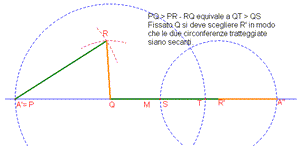
| Figura 2 | Figura 3 |
Ci sono pervenute nove risposte con una partecipazione leggermente superiore da parte della scuola media inferiore rispetto a quella delle superiori. Diamo alle scuole partecipanti il benvenuto o il bentornato alla attività di FLATlandia, invitando i ragazzi che non hanno visto pubblicato il loro lavoro a non demordere, ma a cercare di migliorare di volta in volta le loro risposte.
Queste le scuole che hanno partecipato:
SM “C. A. Dalla Chiesa”, San Genesio ed Uniti (PV)
SM “A. Ferrari”, Maranello (MO)
SM “Bergamaschi” Torrevecchia Pia (PV)
SM “L. da Vinci” Rufina (FI)
SM “Zanella”, Roveredo in Piano (PN)
LS “Benedetto Varchi” Montevarchi (AR) – due risposte
IPSAR “P. Artusi”, Forlimpopoli (FC)
LS “L. da Vinci” Treviso
Nel problema di questo mese abbiamo
proposto una costruzione che apparentemente non presentava difficoltà,
costruire un triangolo di lato assegnato isoperimetrico ad un triangolo
dato. Si chiedeva prima di analizzare le condizioni che rendessero possibile
tale costruzione.
Tale richiesta aveva lo scopo di evitare che venissero presentate soluzioni
trovate in modo sperimentale, senza soffermarsi a riflettere sulla corretta
scelta dei segmenti in gioco.
Le risposte che abbiamo ricevuto sono piuttosto carenti sotto questo
aspetto; si è trascurato di approfondire la ricerca delle condizioni,
dilungandosi piuttosto in elaborate costruzioni.
Qualcuno ha invece semplificato eccessivamente il problema, fornendo la
costruzione richiesta solo in un caso particolare. Le situazioni particolari
vanno eventualmente esaminate dopo aver prodotto una risposta di carattere
generale.
Facendo riferimento alle figure che precedono questo commento, riteniamo
opportuno fare le seguenti precisazioni:
la “disuguaglianza triangolare” afferma che ogni lato è minore della somma degli altri due e da ciò si deduce che PQ deve essere minore del semiperimetro;
dalla “disuguaglianza triangolare” si deduce anche che ogni lato deve essere maggiore della differenza degli altri due quindi, una volta fissato PQ, si deve scegliere R in modo opportuno come illustrato nelle figure;
Precisiamo inoltre che le costruzioni si intendono fatte con riga e compasso, quindi, anche nel caso che si utilizzi il sw Cabri, non è corretto trasportare le misure.
Abbiamo riscontrato una più accurata e completa esposizione in alcune risposte di scuola media rispetto a quelle dei ragazzi di scuola superiore; inoltre, nelle risoluzioni inviate dalla SM “Bergamaschi” e dalla SM “L. da Vinci”, naturalmente sotto la guida degli insegnanti, i ragazzi hanno completato la loro ricerca di costruzione scoprendo il collegamento fra i triangoli isoperimetrici e l’ellisse.
Vengono presentate le seguenti risposte:
SM “Zanella”, nella quale, anche se non giustificate in modo esauriente, vengono analizzate tutte le condizioni che permettono di costruire il triangolo richiesto.
SM “Bergamaschi”, la cui risposta è stata ritenuta esauriente nella prima parte, ma che richiede qualche nostra precisazione nella seconda.
SM “L. da Vinci”, Rufina, di cui, omettendo la descrizione delle operazioni di costruzione già contenute nelle precedenti risposte, riportiamo la premessa con la traccia della soluzione, a testimonianza del metodo di lavoro di quella classe.
NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.
Soluzione proposta da:
Classe 2a A - Scuola Media “Zanella” - Roveredo in Piano (PN)
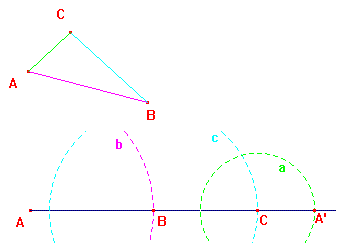
- Riportiamo il perimetro del triangolo
ABC su di una semiretta.
[[…]]
Il segmento AA' [costruito col compasso] è uguale al perimetro del triangolo
dato.
- Ogni lato di un
triangolo è minore della somma degli altri due e maggiore della loro
differenza.
- Disegniamo un triangolo PQR di perimetro AA’: il lato PQ
dovrà essere minore di metà perimetro [affermazione da giustificare].
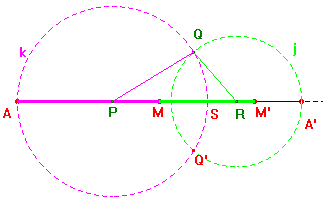
1. Punto medio M di AA’;
2. Punto P sul segmento AM;
3. Circonferenza k di centro P per A (il suo raggio è il lato PQ);
4. S, punto d’intersezione di k con AA’; M’, punto medio tra S ed A’;
5. Punto R sul tratto MM’;
6. Circonferenza j di centro R per A’ (il suo raggio è il lato RQ);
7. Intersezione di k e j: Q, Q’.
Non si può prendere a caso il punto R sul
tratto PA’: escludiamo sicuramente il tratto PM, in questo caso il lato RQ
sarebbe maggiore della somma degli altri due lati; rimane il segmento MA’,
non nel tratto M’A’, il lato PR sarebbe maggiore della somma degli altri due
[quando k e j sono tangenti, R è punto medio di SA’ e PR = PQ + QR].
Concludendo: punto P sul segmento AM (estremi esclusi); punto R sul segmento
MM’ (estremi esclusi).
Soluzione proposta da:
Brambilla Marta, Pirola Selene, Zotti Luca, Ricca Giuseppe,
Gasti Eva, Gambatese Luana, Verdiana Lala
Classe IIIa
M - Scuola Media Statale "Bergamaschi" -
Torrevecchia Pia (PV)


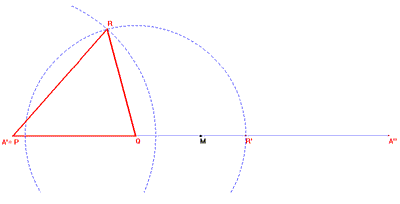
Facendo variare [una volta fissato] Q sul segmento PM, esclusi gli estremi, e [facendo variare] R' sul segmento MA", esclusi gli estremi [affermazione non esatta come si può vedere dalla figura allegata al commento], si ottengono infiniti triangoli con lo stesso perimetro di PQR.
Se, mediante due spilli, fissiamo nei punti P e Q le estremità di un filo lungo 2p – PQ e, tenendo il filo ben teso con una penna, facciamo scorrere la punta della penna sul foglio, otteniamo l’ellisse che ha per fuochi P e Q e tale che per ogni suo punto la somma delle distanze dai fuochi è uguale a 2p – PQ

Disegniamo l’ellisse in un piano
cartesiano [con il sw Cabri]
[[…]]
Soluzione proposta da:
Classe 3aB
- Scuola Media - “L. da Vinci” - Rufina (FI)
In classe abbiamo discusso il problema servendoci di cordicella e aste di
meccano. Abbiamo affrontato l’argomento seguendo le seguenti fasi:
1. Abbiamo stabilito che la cordicella rappresenti il perimetro P di un triangolo qualsiasi ABC.
2. Immediatamente ci siamo accorti che prendendo PQ > P/2 non riusciamo più a chiudere gli estremi della cordicella medesima. Questo vuol dire che per poter costruire il triangolo necessariamente dovremo avere PQ<P/2 [per cui PQ deve essere minore delle somma degli altri due lati].
3. A questo punto abbiamo legato i capi del cordino e considerato una porzione di questo che rispettasse la condizione del punto 2.
Abbiamo poi fissato ad un piano la cordicella con due puntine: la prima puntina rappresenta il punto P, la seconda il punto Q. Con un lapis abbiamo messo la cordicella in tensione in modo che rimanesse descritto un triangolo di vertici P, Q ed R, quest’ultimo rappresentato dal lapis medesimo. Ci siamo quindi accorti che il vertice R è mobile. Nel suo movimento esso assume infinite posizioni a ciascuna delle quali corrisponde un triangolo isoperimetrico a quello di partenza.
Infatti
PQ = costante. Poiché QR + PR = P – PQ, ne consegue che anche QR + PR è costante
4. Ci siamo però accorti che nel movimento del vertice R si verificano due situazioni opposte in cui il triangolo PQR scompare.
Osservando meglio con le aste del meccano questa situazione, ci siamo accorti che il triangolo esiste se un lato è maggiore della differenza degli altri due.
Perciò diremo che se PQ < PR – RQ ( o RQ – PR) il triangolo non si chiude.
Muovendo il vertice R sul nostro modellino, sia nel semipiano superiore che su quello inferiore abbiamo notato che esso descrive una figura particolare: è l’ellisse.
Casi particolari: se i punti P e Q coincidono, il triangolo non esiste, ma si disegna comunque una linea curva, una circonferenza, il cui raggio sarà uguale al semiperimetro del triangolo ABC.
Gli infiniti triangoli PQR ottenuti con questa costruzione hanno tutti uguale base ma altezza variabile con continuità da un valore nullo ad un valore massimo che si ottiene quando il vertice R si trova sull’asse del segmento PQ, per tornare poi a zero. Per questo motivo tra tutti i triangoli isoperimetrici quello di area massima è il triangolo isoscele.
Elenco dei comandi per
realizzare la costruzione:
[[…]]
| Home Page Cabri | Torna a FLATlandia | Archivi |