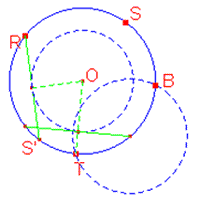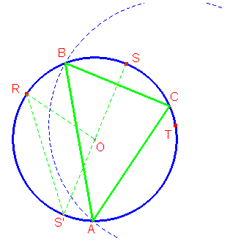
Costruzione: Fissati R,S,T si punta il compasso in T con apertura RS’. La circonferenza ottenuta incontra quella di centro O in A e B. Simmetria assiale di A rispetto OR si trova C.	[Sarebbe più corretto non usare il trasporto di segmento mediante compasso; si può, ad esempio, tracciare la circonferenza di centro O con raggio la distanza di O da RS’e procedere come illustrato nella figura.]

La costruzione è valida anche se R,S,T appartengono alla stessa semicirconferenza. Risultano congruenti gli archi: AT, TB CS, SB CR, RA Il triangolo si riduce ad un segmento se T=S’

---

Abbiamo ricevuto quattordici risposte provenienti dalle seguenti scuole:

• LS “Giovanni Labonia” Rossano (??)

• SM “C.A. Dalla Chiesa” San Genesio ed Uniti (PV)

• LS “Aselli” Cremona (CR)

• SM “G.B. Tiepolo” Milano – tre risposte

• SM “Settembrini” Nova Siri (CS)

• LS “B. Varchi” Montevarchi (AR)

• SM “Bergamaschi” Torrevecchia Pia (PV)

• LS “L. da Vinci” Treviso (TV)

• LS “Farinato”, Enna (EN)

• SM, Istituto Comprensivo di Venasca (CN)

• SM “L. da Vinci” Rufina (FI) – due risposte

In alcune risposte, in maggior parte di scuole medie inferiori, il testo del problema non è stato interpretato in modo corretto: si trattava di prendere (a piacere) tre punti su una circonferenza e di costruire POI il triangolo inscritto che avesse quei punti come punti medi degli archi sottesi dai lati.
Qualcuno ha affermato che, per ottenere il triangolo richiesto, i tre punti non possono appartenere ad una stessa semicirconferenza. Questo è vero solo se si aggiunge la condizione che gli archi che contengono i punti medi non si sovrappongano.
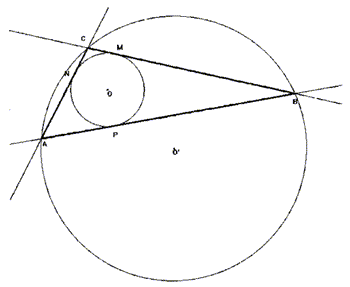
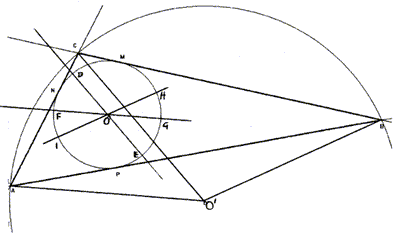
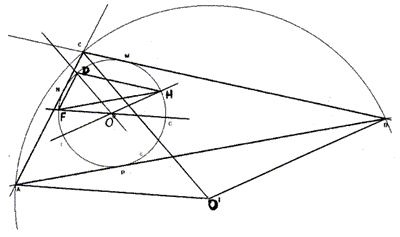
Alleghiamo al testo del problema la costruzione proposta dalla SM “L. da Vinci” (prima figura) con una breve traccia della loro risposta. Nella seconda figura proponiamo una costruzione alternativa basata sulla stessa premessa. Nella terza, da noi ottenuta modificando per trascinamento la prima, si può vedere che la costruzione si applica anche nel caso che i tre punti fissati si trovino in una stessa semicirconferenza. Il triangolo degenera in un segmento quando due dei punti fissati sono estremi di uno stesso diametro.

Gli studenti che hanno affrontato con successo la costruzione hanno dato prova di grande fantasia: varie sono le vie seguite, alcune di notevole efficacia, altre un po’ laboriose, ma tutte testimoniano un apprezzabile interesse per le questioni di geometria.
Facciamo una sintetica esposizione delle varie risoluzioni, in quanto non saranno riportate tutte per motivi di imprecisione o incompletezza nella esposizione o nella presentazione della figura.

• Qualcuno ha “scoperto” il legame fra l’ortocentro del triangolo con vertici nei tre punti medi e l’incentro del triangolo da costruire (SM “Dalla Chiesa”).

• Alcuni hanno cercato il legame fra gli angoli del triangolo da costruire (angoli alla circonferenza)e gli angoli al centro formati dagli assi dei suoi lati (SM “Bergamaschi“ e SM “L. da Vinci”(figura allegata al testo))

• Una risoluzione, semplice nella costruzione, ma piuttosto laboriosa nella giustificazione, è basata sulle relazioni fra gli archi dati e quelli da ottenere.(LS “L. da Vinci”)

• Altri hanno invece considerato il triangolo circoscritto con i lati tangenti nei punti assegnati, simile a quello da costruire, ricorrendo poi a procedimenti diversi: l’omotetia (SM “Tiepolo), il trasporto dell’angolo (LS Aselli), un “teorema” sui triangoli isosceli simili (LS “Farinato”).

NOTA: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.

---

Soluzione proposta da:
Omar Barbieri, Stefano Braschi, Mattia Carioti, Simone Carini, Alessio Mezzadra, Lucilla Zoppi
Classe 3P Scuola Media “C.A. Dalla Chiesa “ - San Genesio ed Uniti (Pavia)

Premessa:
Inizialmente abbiamo cercato un legame tra il triangolo ABC inscritto in una circonferenza ed il triangolo M1M2M3 che si formava unendo i punti medi degli archi sottesi dai lati. Abbiamo trovato due relazioni:

–le bisettrici degli angoli interni di ABC passavano per i punti M1,M2,M3;
–i prolungamenti delle altezze del triangolo M1M2M3 intersecano la circonferenza nei punti A,B,C.

Abbiamo pensato di utilizzare quest’ ultima relazione per la dimostrazione.

Dimostrazione:
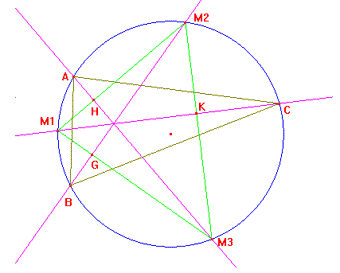
Presi tre punti non allineati M1,M2,M3; costruiamo il triangolo M1M2M3, tracciamo gli assi dei lati, troviamo il circocentro che è il centro della circonferenza circoscritta al triangolo.

Tracciamo le altezze del triangolo M1M2M3 e chiamiamo H,G,K le intersezioni con i lati del triangolo; prolunghiamo le altezze e chiamiamo rispettivamente A,B,C le intersezioni con la circonferenza. Vogliamo dimostrare che i punti A, B e C sono i vertici del triangolo che ha come punti medi degli archi sottesi dai lati i punti M1, M2, M3.

– Dimostriamo che M1 è il punto medio dell’ arco AB:
consideriamo gli angoli alla circonferenza M1M3A ed M1M2B; essi sono uguali perché angoli complementari dell’ angolo M2M1M3 nei triangoli rettangoli M1M2G ed M1M3H.

Siccome sono angoli alla circonferenza della stessa ampiezza, gli archi ad essi sottesi (M1B ed M1A) sono della stessa lunghezza.
Per questo motivo M1 è punto medio dell’ arco AB.
[[…]] [Non occorre ripetere la dimostrazione anche per i punti M2 e M3]

---

Soluzione proposta da:
Classe 3F - Scuola Media “Tiepolo” (Milano)

Dimostrazione

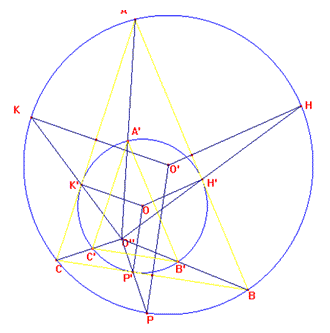
Sulla circonferenza C di centro O ho individuato tre punti: H’, K’, P’; ed ho disegnato i raggi OH’, OK’, OP’, che saranno gli assi del triangolo inscritto.
Ho tracciato tre rette perpendicolari agli assi per i punti prima nominati (H’, K’, P’), ottenendo così il triangolo ABC circoscritto alla circonferenza di centro O. Ho disegnato gli assi di questo triangolo, ottenendo quindi il suo circocentro O’, e ho tracciato la circonferenza circoscritta ad ABC, ottenendo i punti K, H, P, che sono l’intersezione tra [gli assi di ABC] e la circonferenza stessa.
Grazie alle considerazioni precedenti, sappiamo che il triangolo da ricavare è omotetico al triangolo ABC [i lati corrispondenti sono perpendicolari allo stesso segmento].
Per ottenere una omotetia, si deve individuarne il centro; per fare ciò, ho tracciato delle rette passanti per le coppie di punti corrispondenti, quali K e K’, P e P’, H e H’ [sono sufficienti due coppie]; nel punto della loro intersezione O’’ ho ricavato il centro di omotetia. Ho congiunto O’’ con i vertici del triangolo [ABC], e nel punto in cui i segmenti intersecano la circonferenza [di centro O], ho ricavato i vertici del triangolo omotetico richiesto A’B’C’.
[[…]].

---

Soluzione proposta da:
Giacomo Canevari - Classe 2C - Liceo Scientifico “G. Aselli” Cremona

Questa costruzione si basa su una proprietà generale, valida per qualsiasi triangolo ABC di circocentro O.
[[…]]
L’angolo ABC è 1/2 di AOC, che è il suo angolo al centro corrispondente, ed è perciò congruente [nella figura allegata] ad AOM e COM.

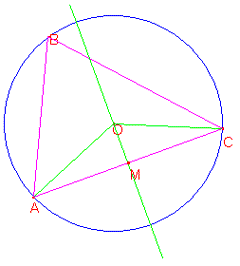
Disegniamo la circonferenza di centro O e prendiamo su di essa tre punti, che chiameremo M, N e P. Essi sono i tre punti medi degli archi sottesi dai lati; sono quindi per definizione equidistanti dagli estremi di ogni lato, cioè appartengono al loro asse. Tracciamo le rette passanti per questi punti e per O, che è anche il circocentro del triangolo cercato, che chiameremo rispettivamente r, s e t: sono gli assi del triangolo. Dovremo perciò fare in modo che i lati del triangolo siano perpendicolari ad essi.
Disegniamo quindi le rette perpendicolari a r, s e t passanti rispettivamente per M, N e P, chiamate r′, s′ e t′, che si intersecheranno nei punti A′, B′ e C′. Il triangolo A′B′C′ è simile a quello cercato ABC.

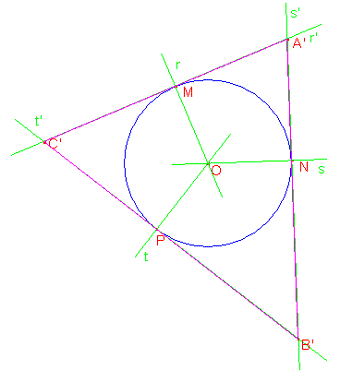
Quindi l’angolo C′A′B′ = CAB (perché corrispondenti di triangoli simili) = POB (per la proprietà prima enunciata). Tracciamo le parallele a s′ e a r′ passanti per O, che intersecheranno la circonferenza in D e in E, poi costruiamo l’asse di PE, che intersecherà la circonferenza in F, e la circonferenza di centro F e raggio FD. L’intersezione tra le due circonferenze è il punto B. Così facendo, infatti, abbiamo riportato l’angolo C′A′B′ tenendo come vertice O e come lato OP [essendo l’arco PB=PF+FB congruente all’arco DE=DF+FE].
Conduciamo da B la perpendicolare a s, trovando sulla circonferenza il punto A, e da A la perpendicolare a r, trovando il punto C. il triangolo ABC è quello cercato.

---

Soluzione proposta da:
Alunni del gruppo "Giochi Matematici"  - Liceo Scientifico "P, Farinato" ENNA
 

Premessa:
E' facilmente dimostrabile la seguente proprietà: "Dati due triangoli isosceli, se i lati congruenti di uno sono paralleli ai lati congruenti dell'altro, i due triangoli sono simili e i terzi lati dei due triangoli risultano paralleli tra di loro".

Soluzione del problema:
Siano M, N e P i tre punti dati e c la circonferenza, di centro O, passante per essi. Consideriamo la tangente alla circonferenza nel punto M e il diametro passante per esso. Tale diametro risulta perpendicolare alla tangente in M e a tutte le corde aventi questo diametro per asse e aventi quindi gli estremi equidistanti da M. Una di queste corde è uno dei lati del triangolo da costruire e la tangente in M è parallela a tale lato.
Considerando le tangenti alla circonferenza c nei tre punti M, N e P si ottiene il triangolo ABC i cui lati, per quanto sopra detto, sono paralleli ai lati del triangolo richiesto.
Consideriamo la circonferenza c1, di centro O', circoscritta al triangolo ABC e tracciamo in essa i raggi: O'A, O'B e O'C. Nella circonferenza c tracciamo i diametri paralleli a O'A, O'B e O'C che secano la circonferenza nei punti D, E, F, G, H, I.
Considerando i triangoli isosceli AO'C e FOD, per la proprietà espressa in premessa, si ha che la corda FD risulta parallela ad AC, tangente in N alla circonferenza c. Allo stesso modo si ha che la corda DH risulta parallela alla tangente in M e la corda FH risulta parallela alla tangente in P.
Il triangolo DFH è il triangolo cercato [anche il triangolo GEI].

Consideriamo una circonferenza di centro O e su di essa si prendano i tre punti M, N, P

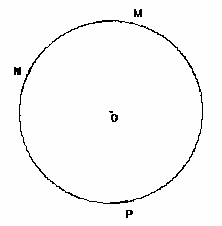
Si tracciano le tangenti alla circonferenza nei punti M, N e P e si considera il triangolo ABC

 

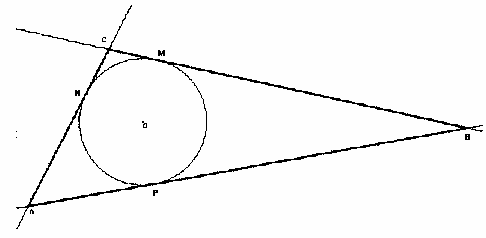
Si costruisce la circonferenza di centro O' circoscritta al triangolo ABC e si tracciano i raggi O'A, O'B, O'C

Si tracciano le rette parallele ai raggi O'A, O'B e O'C passanti per O. Si ottengono i punti D, E, F, G, H, I

Il triangolo DFH è il triangolo cercato