 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Maggio 2004
Dato un angolo convesso di vertice V, sia A un qualunque punto di tale angolo.
a) Costruire le circonferenze
(la circonferenza) passanti per A e tangenti ai lati dell’angolo.
b) Giustificare la costruzione effettuata.
NOTA di Gennaio 2005:
Poiché i ragazzi della scuola media non avevano
giustificato la loro costruzione proponemmo, a chi avesse voluto farlo, di
inviarci, entro il 30 Settembre 2004, una dimostrazione della proprietà da essi
utilizzata.
Abbiamo riproposto il termine del 31 Dicembre, ma non abbiamo ricevuto risposte.
Ecco una traccia della nostra proposta di risoluzione in formato PDF: Seleziona QUI per scarcarla
COMMENTO
Sono giunte tre risposte da studenti delle seguenti scuole:
Nel problema si chiedeva di costruire le circonferenze
tangenti ai lati di un angolo convesso, di vertice V, passanti per un punto A
appartenente all’angolo. La genericità del punto assegnato doveva portare i
solutori ad esaminare tutte le sue possibili posizioni.
Si chiedeva poi di giustificare la costruzione eseguita.
Nessuna delle risposte pervenute è completa. Esaminiamole una per volta.
- SM “C. A. Dalla Chiesa”: alcuni ragazzi
della classe 3P hanno fornito una bella costruzione del caso generale nel senso
classico del termine, cioè eseguibile con “riga e compasso”. Hanno osservato che
la retta VA interseca le circonferenze tangenti ai lati di un angolo in punti
che, congiunti con i rispettivi centri, formano triangoli simili.
Hanno poi preso in esame solo il caso particolare che A sia sulla bisettrice,
senza però darne la costruzione.
Non hanno giustificato la loro costruzione, come richiesto nel punto (b), ma
questo non è obbligatorio per gli studenti della scuola media inferiore [vedi
NOTA 1].
- LS “G. Aselli”: Giacomo Canevari ha invece
eseguito una Cabri-costruzione. Egli ha osservato che, se una circonferenza perA
è tangente ai lati di un angolo, il suo centro è equidistante da A e da ciascun
lato. Deve quindi appartenere, oltre che alla bisettrice dell’angolo, alla
parabola con fuoco in A e direttrice uno dei lati dell’angolo.
Ha giustificato la sua costruzione; non ha considerato il caso particolare in
cui A appartiene alla bisettrice.
Non essendo possibile costruire per punti una curva continua, solo con un
software, come ad esempio Cabri, si possono (apparentemente) visualizzare le
intersezioni della parabola con la bisettrice dell’angolo.
- ITI “Berenini”: gli studenti della classe
2B hanno prima preso in esame il caso particolare in cui A appartiene alla
bisettrice, proponendone una corretta costruzione.
Hanno poi considerato il caso in cui A non sia sulla bisettrice (e neppure su un
lato); hanno valutato le condizioni che caratterizzano le circonferenze
richieste, ma la costruzione allegata non è corretta.
Ricordiamo a questi ragazzi che una costruzione eseguita con Cabri è valida solo
se non perde le sue proprietà per trascinamento dei suoi punti liberi; inoltre
deve essere giustificata.
Altre eventuali osservazioni saranno riportate in parentesi quadra nel testo delle risposte.
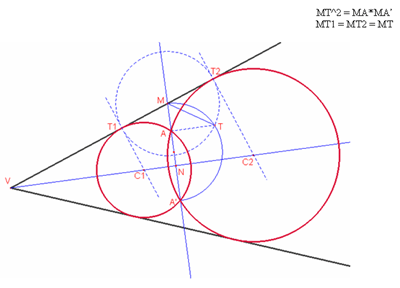
Nella figura allegata al testo del problema viene illustrata una costruzione del tipo “riga e compasso” in cui si fa ricorso al teorema detto “della tangente e della secante”.
SOLUZIONI
Soluzione proposta da:
Stefano Braschi, Fabio Fischetti, Mattia Carioti, Lucilla Zoppi
Classe 3P, Scuola media “C.A. Dalla Chiesa” - San Genesio ed Uniti ( PV)
Dopo aver costruito l’angolo convesso di vertice V
prendiamo un punto A qualunque di questo. Tracciamo la bisettrice dell’angolo.
[Si poteva eventualmente costruire].
Dato che la circonferenza passante per A deve essere tangente ai lati
dell’angolo, il suo centro deve trovarsi sulla bisettrice, perché luogo dei
punti equidistanti dai lati dell’angolo. Tutte le circonferenze tangenti ai lati
dell’angolo hanno i centri sulla bisettrice e sono omotetiche tra loro (in una
omotetia di centro V) [Solo se considerate a due a due, non esiste un unico
rapporto di omotetie per tutte le circonferenze]. Tra queste ci sono quelle
tangenti ai lati e passanti per A.
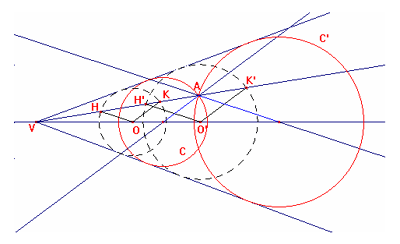
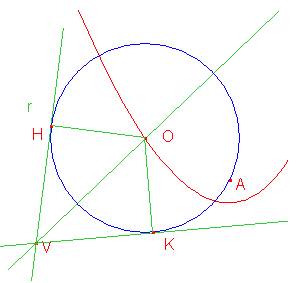
Costruiamo due circonferenze tangenti ai lati dell’angolo, mandando da due punti
qualsiasi del lato dell’angolo la perpendicolare al lato stesso, le intersezioni
di queste perpendicolari con la bisettrice sono i centri delle due circonferenze
(una di centro O e una di centro O’). Tracciamo la semiretta di origine V e
passante per A. Questa semiretta interseca le circonferenze in quattro punti (H
e K ed H’ e K’). Notiamo che i raggi HO e H’O’, KO e K’O’ sono paralleli tra
loro. Allora per trovare i centri delle circonferenze passanti per A e tangenti
ai lati dell’angolo, costruiamo le rette passanti per A e parallele ai raggi OK
e OH. Le intersezioni di queste due rette con la bisettrice dell’angolo di
vertice V saranno i centri delle circonferenze che cerchiamo. Queste sono
secanti nel punto A.
Se il punto A si trovasse sulla bisettrice, le due circonferenze sarebbero tangenti tra loro in questo punto. [Perché? Come si costruiscono?]
Soluzione proposta da:
Giacomo Canevari
Classe 2C, Liceo scientifico “G. Aselli” Cremona (CR)
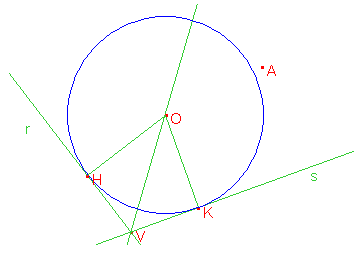
Disegniamo due rette r e s incidenti in un punto V, poi prendiamo un punto qualsiasi A appartenente ad uno degli angoli convessi così creati. Consideriamo una circonferenza di centro O tangente alle due rette e indichiamo i due punti di tangenza con H e K. Sappiamo che OH = OK perché raggi, l’angolo VKO = VHO = 90°, OV è in comune: perciò i triangoli rettangoli VHO e VKO sono congruenti per il quarto criterio. Allora gli angoli OVH e OVK sono congruenti, dunque O appartiene alla bisettrice di HVK.
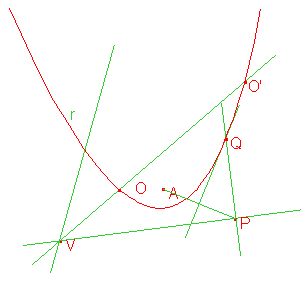
Costruiamo quindi la bisettrice dell’angolo [si poteva
indicare come costruirla].
Su di essa dobbiamo considerare un punto O tale che, chiamata K la sua
proiezione su s, OK = OA: dobbiamo cioè trovare un punto equidistante dalla
retta s e da A. Tale punto apparterrà dunque alla parabola di fuoco A e
direttrice s.
Possiamo costruire la parabola come luogo di punti: consideriamo su s un punto P
a piacere, poi tracciamo la perpendicolare ad s per P e l’asse del segmento AP.
Le due rette si intersecheranno in un punto Q, equidistante da A e da s: il
luogo descritto da Q al variare di P è la parabola cercata.
Le intersezioni tra la parabola e la bisettrice dell’angolo, che chiameremo O e O`, sono i centri delle circonferenze cercate. Sappiamo che AO = OK, dove K è la proiezione di O sulla retta s, per costruzione; inoltre, se consideriamo la distanza OH di O dalla retta r, risulta OH = OK perché i triangoli OVH e OVK sono congruenti per il quarto criterio. Infatti gli angoli HVO e KVO sono congruenti per ipotesi, VHO = VKO = 90°, il segmento OV è in comune. Da ciò si ricava che AO = OH = OK, perciò per i tre punti passa una circonferenza di centro O. Analogo ragionamento si può fare per il punto O`.
Casi particolari:
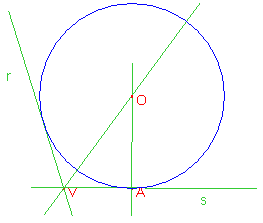
Il punto A appartiene alla retta s, ma non a r. In tal caso, la parabola degenere di fuoco A e direttrice s corrisponde alla perpendicolare ad s passante per A, perciò il punto O, centro della circonferenza cercata, corrisponde all’intersezione fra tale perpendicolare e la bisettrice dell’angolo dato.
Il punto A appartiene alla retta r, ma non a s. Procediamo in modo analogo a prima, ma costruiamo ora la parabola di direttrice r e fuoco A: ricadiamo quindi ancora nel primo dei casi particolari esaminati. Perciò, anche in questo caso, esiste una sola circonferenza che soddisfa le richieste del problema.
Il punto A coincide con V. In tal caso, la circonferenza richiesta è degenere e si riduce al solo punto V.
Soluzione proposta da:
classe 2B st, I.T.I.S. “Berenini”
Fidenza (PR)
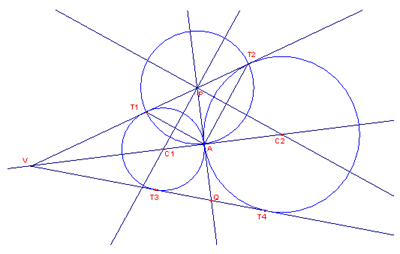
Dato l’angolo di vertice V e lati a e b si tracci la sua
bisettrice [si poteva eventualmente costruire].
Si possono presentare due casi:
1) il punto A appartiene alla bisettrice
2) il punto A non appartiene alla bisettrice.
Nel primo caso si conduce la retta per A perpendicolare
alla bisettrice [perché? Questo passaggio doveva essere giustificato] e si
indicano con P e Q le sue intersezioni con i lati a e b dell’angolo. Puntando il
compasso in P con raggio PA trovo i punti T1 e T2 di intersezione di questa
circonferenza con il lato a dell’angolo.
Il punto C1 di intersezione dell’asse del segmento T1A con la bisettrice
dell’angolo dato è il centro di una delle circonferenze richieste il cui raggio
è dato da C1A=C1T1. Infatti essendo punto dell’asse di T1A è equidistante dagli
estremi perciò CT1=CA ed essendo sulla bisettrice dell’angolo dato è
equidistante dai suoi lati perciò C1T1=C1T3.
Analogamente il punto C2 di intersezione dell’asse del segmento T2A con la
bisettrice dell’angolo dato è il centro dell’altra circonferenza richieste il
cui raggio è dato da C2A=C2T2.
Nel caso A non appartenga alla bisettrice [[…]] [vedi commento]
| Home Page Cabri | Torna a FLATlandia | Archivi |