FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Febbraio 2004

E’ dato un segmento AB e l’asse r di esso.
Si prenda un qualunque punto P su AB ed un qualunque punto Q su r.

1. Dimostrare che: AP*PB = QA2 – QP2

2. Nel caso che sia P sul prolungamento di AB, come deve essere modificata la relazione data?

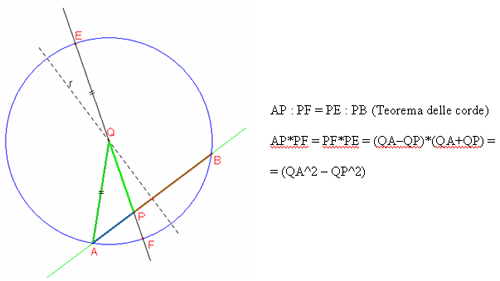
COMMENTO

Abbiamo ricevuto nove risposte da studenti di cinque scuole secondarie inferiori e due superiori:

• LS “G. Aselli”, Cremona (CR) – due risposte
• SM “G.B.Tiepolo”, Milano (MI) – due risposte
• SM “Bergamaschi”, Pavia (PV)
• SM “G. Zanella”, Roveredo in Piano (PN)
• SM “I. Nievo”, Cordignano (TV)
• SM “C.A. Dalla Chiesa”, S. Genesio ed Uniti (PV)
• LS “B. Varchi”, Montevarchi (AR)

Nel problema, dato un segmento AB e il suo asse, preso un punto P sulla retta AB ed un punto Q sull’asse, si chiedeva di dimostrare l’uguaglianza fra il prodotto delle misure di due segmenti (con un estremo in P e l’atro in A o B) e la differenza fra le misure dei quadrati di altri due (con un estremo in Q e l’atro in A o P). Si chiedeva inoltre di distinguere i due casi in cui P fosse all’interno o sul prolungamento di AB.
Il modo in cui è stato posto il quesito ha indotto, in alcune risposte, il ricorso a un metodo di risoluzione algebrico, basato sulla applicazione del teorema di Pitagora o del secondo teorema di Euclide.
In altre invece dopo l’uso del teorema di Pitagora si è utilizzata l’equivalenza di superfici, interpretando geometricamente sia il prodotto dei segmenti sia la differenza dei quadrati.
Una simpatica interpretazione è stata fatta dai ragazzi della Scuola Media di Roveredo in Piano, classe 2A, che hanno immaginato di ritagliare i quadrati su cartoncino e di porli sui piatti di una bilancia per verificare che differenze di superfici equivalenti sono ancora equivalenti.
Nella prima parte qualcuno ha considerato il punto P sulla prima metà di AB, qualcuno sulla seconda; pochi si sono chiesti se la relazione rimanesse invariata modificando la posizione di P.
Questa situazione viene risolta (inconsciamente) nella risposta della Scuola Media di Cordignano che verrà di seguito presentata.
Una interpretazione geometrica, del caso in cui P sia interno ad AB, diversa da quelle proposte, viene da noi illustrata nella figura allegata al testo del problema. Per il caso in cui P sia esterno ad AB vedere la NOTA 1.

Per fornire un quadro completo delle risoluzioni giunte, abbiamo stabilito di presentare le seguenti risposte:

• LS “B. Varchi”, come esempio di risoluzione algebrica. Risposte simili, ma contenenti imprecisioni, sono quelle inviate dagli studenti del LS “G. Aselli”, dalla SM “Bergamaschi”, dalla SM “G.B. Tiepolo” (Velia Cavallini).
• SM “C.A. Dalla Chiesa”, la prima parte, in cui si fa ricorso al II teorema di Euclide.
• SM “I. Nievo”, come esempio di interpretazione geometrica della prima parte; in essa, mediante una simmetria, vengono implicitamente contemplate entrambe le possibilità (vedi commento).
• SM “G.B. Tiepolo” (Giacomo Compagnoni), come esempio di risoluzione geometrica della seconda parte.

NOTA 1: Una interessante interpretazione geometrica della seconda parte è stata fornita da uno studente del LS “P. Farinato” di Enna. Tale studente frequenta il quinto anno, quindi la sua risposta non viene menzionata nel commento in rispetto al regolamento di FLATlandia. Chi fosse interessato a scaricarla in formato Adobe Acrobat può selezionare qui.

NOTA 2: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.

Soluzione proposta da:
Luca Visani - Classe 2C, Liceo scientifico “B. Varchi” - Montevarchi (AR)

1) Prendo il punto P ad esempio compreso tra A ed M, il punto medio di AB.
Si nota che AP = AM-PM e PB = PM+MB, ed essendo, per ipotesi, MB congruente ad AM, risulta che PB = AM+PM.
Quindi AP*PB = (AM-PM)(AM+PM) = AM^2-PM^2.

Si considera poi il triangolo rettangolo AMQ [essendo MQ sull’asse di AB]; per il teorema di Pitagora, si ha:
QA^2 = AM^2+QM^2.
Sempre dal teorema di Pitagora, però nel triangolo PMQ, si ha: QP^2 = PM^2+QM^2; dunque risulta che QA^2-QP^2 = AM^2+QM^2-(PM^2+QM^2) = AM^2+QM^2-PM^2-QM^2 = AM^2-PM^2.

Siccome AP*PB = AM^2-PM^2 e QA^2-QP^2 = AM^2-PM^2, si ha che AP*PB = QA^2-QP^2.

2) Prendo il punto P sul prolungamento di AB dalla parte di B.
AP = AB+PB, quindi AP*PB = (AB+PB)*PB = AB*PB+PB^2.

Sapendo che
QA^2 = AM^2+QM^2 e QP^2 = PM^2+QM^2 = (MB+PB)^2+QM^2 = MB^2+PB^2+2MB*PB+QM^2,

risulta che
QP^2-QA^2 = MB^2+PB^2+2MB*PB+QM^2-(AM^2+QM^2) = MB^2+PB^2+2MB*PB+QM^2-AM^2-QM^2 = PB^2+2MB*PB = PB^2+AB*PB.

La relazione data diventa quindi
AP*PB = QP^2 – QA^2

Soluzione proposta da:
Braschi Stefano, Carioti Mattia, Zoppi Lucilla
Classe 3P, Scuola media “C.A. Dalla Chiesa” - S. Genesio ed Uniti (PV)

PRIMO CASO [[…]]

Poiché QA^2=QM^2+AM^2 e QP^2=QM^2+PM^2 si ha che QA^2-QP^2=QM^2 +AM^2-(QM^2+PM^2)=QM^2+AM^2-QM^2-PM^2=AM^2-PM^2

Ora si tratta di dimostrare che AP*PB=AM^2-PM^2

Abbiamo considerato il cerchio avente come diametro AB. Chiamiamo C il punto della circonferenza la cui proiezione sul diametro AB sia P.

ABC è rettangolo [in C], poiché inscritto in una semicirconferenza.

Per il teorema di Euclide possiamo scrivere:
AP*PB=CP^2
Applicando il teorema di Pitagora al triangolo [CPM], si ha che:
AP*PB=CP^2=CM^2-PM^2
Siccome CM è raggio e quindi uguale ad AM, possiamo scrivere:
AP*PB=CP^2=AM^2-PM^2, che è quello che volevamo dimostrare.

SECONDO CASO

[…]

Soluzione proposta da:
Christian Rosolen, Silvia Grillo, William Zancan.
Classe II C - Scuola media di Cordignano (TV)

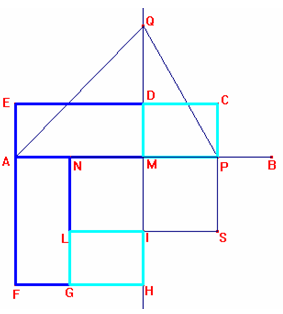
Si consideri il triangolo AQM rettangolo in M per costruzione (definizione di asse)
AQ^2=AM^2+QM^2 per il teorema di Pitagora.

Si consideri il triangolo rettangolo (per costruzione) MPQ, per il teorema di Pitagora
PQ^2=MP^2+QM^2 per cui
AQ^2-PQ^2=AM^2+QM^2-(MP^2+QM^2) quindi AQ^2-PQ^2=AM^2-MP^2

Si costruisca sul segmento AP il rettangolo APCE di superficie AP*PB, con PC=PB per costruzione. Tale rettangolo è equivalente, per il principio di equiscomponibilità , alla somma dei rettangoli EDMA e MPCD.

Si costruisca [il quadrato MPSI e si consideri il suo] simmetrico [[…]] rispetto all’asse r.
La superficie del rettangolo APCE deve essere uguale alla differenza delle superfici dei quadrati AFHM e NLIM .

Per dimostrare questo si prolunghi il lato NL fino ad incontrare il lato FH in G.
Poiché MB=MA=MH e MP=MN=MI per costruzione, risulta che AN=PB=IH per differenza di segmenti congruenti.

Il rettangolo EDMA risulta equivalente al rettangolo ANGF perché hanno congruenti i segmenti.
AF=NG=ED=AM, AN=FG=EA=DM.

Il rettangolo LGHI risulta equivalente al rettangolo DCPM perché DM=CP=IH=GL,DC=MP=GH=LI.

Come volevasi dimostrare.

Soluzione proposta da:
Giacomo Monzio Compagnoni
Classe 3F, Scuola Media “G.B. Tiepolo” - Milano

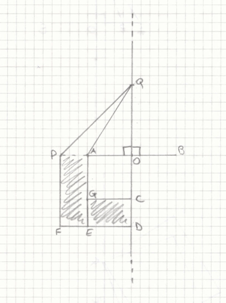
Prima parte
[[…]]

Seconda parte

Nel caso che P sia sul prolungamento di AB la relazione diventa AP * PB = QP^2 – QA^2.
Questo per lo stesso ragionamento esposto precedentemente.
PQ^2 = QO^2 + OP^2
AQ^2 = AO^2 + QO^2
Quindi:
QP^2 – QA^2 = OP^2 – AO^2
CDEG e EFPA sono due rettangoli con stessa [congruente] altezza che possono formare un rettangolo unico con altezza AP e con base PF + ED.
PF = PO
ED = AO = OB (essendo r asse di AB, come già detto nella prima parte)
PO + OB = PB
Conseguentemente alle tre affermazioni precedenti il rettangolo formato ha dimensioni uguali a AP e PB.
Poiché QP^2 – QA^2 = OP^2 – AO^2 e OP^2 – AO^2 = AP * PB, QP^2 – QA^2 = AP * PB

| Home Page Cabri | Torna a FLATlandia | Archivi |