 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Dicembre 2003
Il testo del problema:
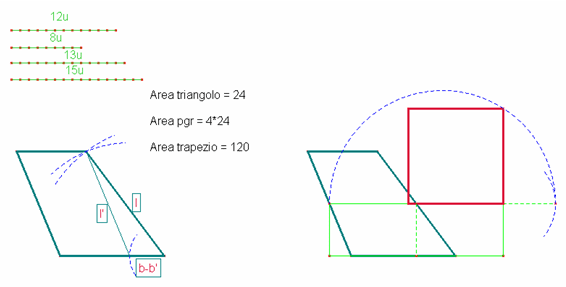
a) Fissata una unità di misura u, costruire il trapezio le cui basi misurano 12u e 8u ed i lati obliqui 13u e 15u.
b) Calcolare l’area del trapezio.
c) Indicare una costruzione che trasformi il trapezio ottenuto in un quadrato ad esso equivalente.
COMMENTO
Abbiamo ricevuto sei risposte, di cui solo due da scuole secondarie superiori. Forse l’argomento dell’equiscomponibilità non è ancora stato affrontato nelle scuole superiori i cui studenti hanno di tanto in tanto partecipato a FLATlandia.
Queste le scuole:
Nel problema proposto si chiedeva di costruire un
trapezio, date le misure delle basi e dei lati obliqui, di calcolarne l’area e
di trasformarlo poi in un quadrato equiesteso. Nelle risposte inviate dalle
scuole medie “Tiepolo” e “Leonardo da Vinci” la costruzione iniziale è stata
risolta utilizzando direttamente i segmenti assegnati.
In quelle inviate dalle scuole medie “C.A. Dalla Chiesa” e “Bergamaschi” sono
state prima analizzate le caratteristiche della figura risultante, prolungandone
i lati obliqui e ricorrendo alla similitudine, per dedurne poi una costruzione
che, però, viene descritta solo dai ragazzi della SM “Bergamaschi”.
Gli studenti di scuola superiore o non hanno affrontato in modo corretto (LS “B.
Varchi”) questa prima costruzione oppure hanno privilegiato un percorso
algebrico (LS” P. Farinato”) per individuare condizioni di esistenza del
trapezio, senza descriverne poi la costruzione.
Anche il calcolo dell’area del trapezio ottenuto è stato realizzato in modo diverso: applicazione della formula di Erone ad un opportuno triangolo, per i ragazzi di scuola media; determinazione dell’altezza mediante equazioni, per gli studenti di scuola superiore.
La terza parte, cioè la trasformazione del trapezio in quadrato, è stata risolta principalmente trasformando il trapezio in un rettangolo e successivamente nel quadrato richiesto, utilizzando uno dei teoremi di Euclide. Fanno eccezione i ragazzi del LS “P. Farinato”, come si può vedere dalla loro risposta. Di ciascuna delle risposte presenteremo le parti che abbiamo ritenuto più significative.
NOTA 1: Le nostre correzioni od osservazioni sono contenute in parentesi quadra. Con doppia parentesi quadra vengono indicate le parti omesse.
NOTA 2: Allegare alle risposte le corrispondenti figure, per una miglior comprensione del testo in caso di errori nelle loro descrizioni.
Soluzione proposta da:
Giacomo Monzio Compagnoni
Classe 3F - S.M. “Tiepolo” - Milano (MI)
[Si fa riferimento alla prima figura precedente al
commento]
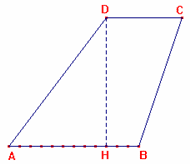
a) Per disegnare il trapezio [ho prima costruito] il triangolo avente
come base la differenza tra le basi del trapezio e, come lati [[…]], i lati
obliqui del trapezio.
Ho disegnato la sua base e ho tracciato due circonferenze aventi come centri gli
estremi della base e ho trovato il punto di intersezione tra loro che insieme ai
due estremi della base è un vertice del triangolo.
Ho [prolungato] la base del triangolo fino a che ha misurato 12U [come la] base
maggiore del trapezio. Ho considerato il lato del triangolo avente un estremo in
comune con un estremo della base di 12 U uno dei lati del trapezio e per
tracciare l’altro lato ho tracciato la parallela all’altro lato del triangolo
passante per l’altro estremo della base di 12 U. Ho tracciato la parallela alla
base maggiore passante per l’estremo del primo lato obliquo [[…]], e ho trovato
il punto di intersezione tra questa retta e l’altro lato obliquo che è l’ultimo
vertice del trapezio.
b) [[…]]
c) [[…]]
Soluzione proposta da:
Classe 3B - Scuola Media “L. da Vinci” - Rufina (FI)
a) Non avendo tra i dati di partenza alcun angolo, abbiamo considerato il trapezio ABCD richiesto come costituito da un triangolo (avente come base la differenza delle basi del trapezio (AB-CD) e gli altri due lati congruenti a quelli del trapezio), e da un parallelogramma avente la base congruente alla base minore assegnata e il lato obliquo coincidente con uno dei lati del triangolo. E’ quindi evidente che i trapezi che si possono così disegnare sono 2, a seconda del lato obliquo scelto per individuare la parallela.
Elenco dei comandi per la costruzione
Abbiamo costruito 4 segmenti AB, CD, BC e AD, che sono misurano 12u, 8u, 15u e 13u, stabilito un segmento unitario (u) che abbiamo utilizzato con unità di misura.
1) Retta r
2) Punto A su di essa
3) Compasso, apertura congruente alla differenza delle basi e centro in A, si
individua A’ all’intersezione della retta con la circonferenza.
4) Compasso, apertura lato obliquo1 e centro in A.
5) Compasso, apertura lato obliquo2 e centro in A’.
6) Punto D all’intersezione delle due circonferenze.
7) Parallela ad r passante per D.
8) Compasso, apertura congruente alla base minore, centro in D, si individua il
punto C.
9) Parallela al lato obliquo2 passante per C, individuo il punto B
all’intersezione della parallela con la retta r.
10) Poligono ABCD
b) [[…]]
c) Per trasformare il trapezio ABCD nel quadrato ad esso equivalente siamo passati attraverso una figura intermedia, il rettangolo equivalente a cui potremo applicare il 1° teorema di Euclide.
Da trapezio scaleno a rettangolo
Per realizzare questa trasformazione abbiamo operato alcuni passaggi fondamentali:
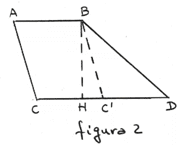
1) Individuare su uno dei lati obliqui, CB, il punto medio M e tracciare la parallela alla base AB passante per M individuando così il punto K all’intersezione della parallela con il lato obliquo AD.
2) Tracciare la perpendicolare alla base minore CD passante per un punto L appartenente ad essa in modo tale che la sua proiezione, N, appartenga alla base maggiore AB; punto O intersezione di LN con la retta MK.
Il trapezio rimane diviso così in due coppie di trapezi
rettangoli, NBMO e MCLO, ANOK e DKOL aventi a due a due il lato obliquo
congruente e gli angoli uguali perché corrispondenti in quanto descritti da
rette parallele (AB, CD, MK) tagliate da una stessa trasversale (
rispettivamente CB e AD):
DAB = DKM; AKM = ADC; ABC = KMC; KMB = DCB,
e supplementari perché coniugati interni:
KMC + KMB = 180°; BCD + ABC = 180°; DKM + AKM = 180°; DAB + ADC = 180°
La simmetria centrale dei poligoni NBMO e ANOK intorno ai punti medi M e K, porta:
a) la esatta sovrapposizione dei lati obliqui, MB su MC,
AK su KD,
b) gli angoli supplementari, adiacenti (ABC adiacente con BCD, BMK adiacente con
KMC ecc.)
c) la perpendicolare a CD, LN, nelle perpendicolari HE e GF, ancora a CD .
Da a) e b) consegue l’allineamento dei punti H e G,
simmetrici di N rispetto ad i punti M e K, sulla retta CD, e in modo analogo dei
punti E ed F, simmetrici di O, sulla retta MK.
La figura che se ne ottiene è il rettangolo EFGH (punto c), equivalente, con il
trapezio di partenza perché equicomposto con esso.
Nota: nel problema abbiamo scelto di posizionare il punto
L in modo che la sua proiezione ortogonale appartenga alla base maggiore per
semplificare la dimostrazione che ne consegue.
Infatti se il punto N cade esternamente alla base maggiore il rettangolo EFGH si
forma comunque ma i trapezi ANOK, KOLD, NBMO e OMCL degenerano in poligoni
intrecciati e non per cui diventa laborioso giustificare l’equivalenza del
trapezio ABCD e del rettangolo EFGH.
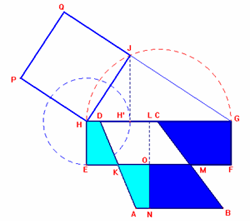
Da Rettangolo a quadrato
Per operare questa trasformazione ci siamo avvalsi del I°
Teorema di Euclide.
Sia la dimensione maggiore del rettangolo, HG, ipotenusa del triangolo
rettangolo HGJ inscritto nella semicirconferenza di uguale diametro.
Sia inoltre H’il punto ottenuto su HG facendo centro in H con apertura HE. Il
segmento HH’ così individuato è la proiezione del cateto HJ.
Si procede alla costruzione di quest’ultimo tramite la perpendicolare ad HG, per
H’che individua sulla semicirconferenza il punto J.
Il quadrato HJQP costruito sul cateto HJ è la figura richiesta dal problema.
Soluzione proposta da:
Marta Brambilla e Selene Pirola
Classe 3M - S.M.“Bergamaschi” - Torrevecchia Pia (PV)
a) Prima di eseguire la costruzione richiesta,
osserviamo che, prolungando i lati obliqui del tra-pezio, otteniamo due
triangoli simili. Chiamiamo E l’intersezione dei prolungamenti dei lati obliqui
AD e BC.
I triangoli ABE e DCE sono simili per il primo criterio di similitudine perché
hanno:
l’angolo AEB in comune
angolo EDC = angolo EAB perché angoli corrispondenti formati dalle parallele
AB e DC tagliate dalla trasversale EA
angolo ECD = angolo ABE perché se due triangoli hanno rispettivamente
congruenti due angoli, hanno congruente anche il terzo, essendo la somma degli
angoli interni di un triango-lo 180°
quindi possiamo scrivere AE : DE = BE : CE = AB : DC e, per la proprietà dello
scomporre,
(AE - DE) : AE = (BE – CE) : BE = (AB – DC) : AB ossia per il nostro trapezio
sarà
15 : AE = 13 : BE = 4 : 12 da cui ricaviamo AE=45u e BE=39u
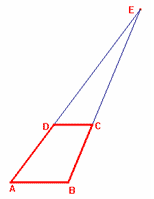
Per costruire il trapezio fissiamo una unità di misura u e [[…]] disegniamo i seguenti segmenti:
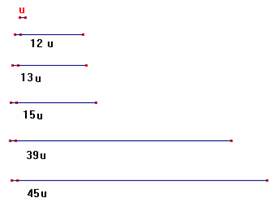
Costruiamo quindi il triangolo ABE i cui lati misurano
45u, 39u, 12u.
Otteniamo il punto D come intersezione di AE con la circonferenza di centro A e
raggio 15u.
In modo analogo otteniamo il punto C, intersezione di BE con la circonferenza di
centro B e raggio 13u.
[[...]]
DC inoltre, per il rapporto di similitudine, misura 8u.
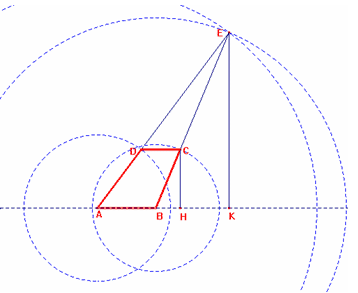
b) Per calcolare l’altezza CH del trapezio, calcoliamo prima l’altezza EK del triangolo ABE, che ricaviamo dopo aver calcolato l’area mediante la formula di Erone.
![]()
EK = 216.2:12 = 36u
Poiché i triangoli CBH e EBK sono simili per il primo
criterio di similitudine, essendo CHB = EKB=90° e l’angolo CBH in comune,
possiamo scrivere EK : CH = BE . BC e quindi
36 : CH = 39 : 13 da cui CH = 12u
Area(ABCD) = (12 + 8) * 12 : 2u2
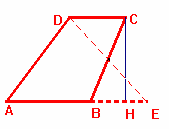
c) Costruiamo il corrispondente del segmento DC nella simmetria centrale di centro il punto medio di BC. Il trapezio è equivalente al triangolo ADE avente per base la somma delle basi del trapezio e per altezza l’altezza del trapezio.
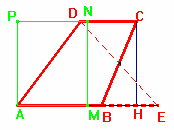
Costruiamo ora il rettangolo AMNP dove M è il punto medio di AE. Tale rettangolo è equivalente al triangolo AED e, per la proprietà transitiva della relazione “equivalenza”, è equivalente al trapezio ABCD
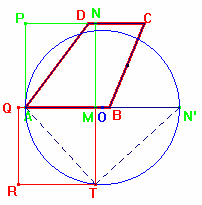
Indichiamo con N’ il punto di intersezione della
circonferenza di centro M e raggio MN con la retta AB e con O il punto medio di
AN’.
Disegniamo la circonferenza di centro O e raggio ON’ e, tracciata la
perpendicolare ad AN’ passante per M, indichiamo con T una delle due
intersezione con la circonferenza.
Nel triangolo ATN’, rettangolo perché inscritto in una semicirconferenza, TM è
l’altezza re-lativa all’ipotenusa.
Per il secondo teorema di Euclide, il quadrato costruito su TM è equivalente al rettangolo avente per dimensioni le proiezioni dei cateti sull’ipotenusa, ma essendo MN’=MN è an-che equivalente al rettangolo AMNP, che a sua volta è equivalente al trapezio ABCD.
Soluzione proposta da:
Classe 3P - S.M. “C.A. Dalla Chiesa” - San Genesio ed Uniti (PV)
a) [[…]] [simile a SM “Bergamaschi”; costruzione non descritta]
b) [manca il calcolo dell’area]
c) Ora trasformiamo il trapezio in un triangolo equiesteso:
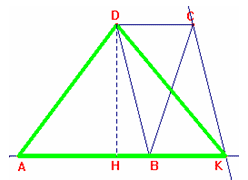
tracciamo la diagonale DB e la parallela ad essa passante
per C; prolunghiamo il lato AB e chiamiamo K il punto di intersezione tra il
prolungamento e la retta. Uniamo D con K.
Il triangolo AKD è equiesteso al trapezio per somma di superfici [equiestese in
quanto] congruenti (DCB=DBK; il trapezio ABCD=ADB+DBC, il triangolo ADK=ADB+DBK)
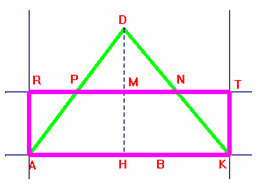
Ora trasformiamo il triangolo ADK in un rettangolo ad esso
equiesteso:
troviamo il punto M ( il punto medio di DH), tracciamo la retta parallela ad AK
passante per M e poi mandiamo le perpendicolari a questa retta passanti per A e
K. Chiamiamo R e T le loro intersezioni.
Il rettangolo AKTR è equiesteso al triangolo ADK per somma di [superfici]
equiestese:
il rettangolo AKTR=AKNP+ARP+NTK, il triangolo AKD=AKNP+PMD+DMN, i triangoli RPA
e PMD [congruenti] poiché AP=PD e gli angoli APR=DPM poiché angoli opposti al
vertice(la stessa cosa avviene per i triangoli KTN e MND ).
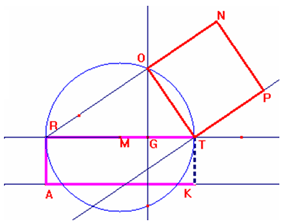
Ora trasformiamo il rettangolo in un quadrato
ad esso equiesteso sfruttando [il primo] teorema di Euclide:
[con centro nel punto medio del lato RT] (M) tracciamo una circonferenza
passante per R e T. Ora riportiamo l’ altezza TK del rettangolo sul lato RT
utilizzando il compasso, e per il punto G ottenuto mandiamo la perpendicolare al
lato RT. Il punto di intersezione di questa con la circonferenza lo chiamiamo O.
Disegniamo il triangolo ROT che sappiamo
essere rettangolo poiché inscritto in una
semicirconferenza. Costruiamo il quadrato sul cateto OT che è equiesteso, per il
primo teorema di Euclide, al rettangolo avente come dimensioni l’ ipotenusa RT e
la proiezione del cateto sull’ ipotenusa.
Questo quadrato è equiesteso al trapezio
iniziale per la proprietà transitiva dell’ equiestensione.
[[...]]
Soluzione proposta
da:
Luca Visani
Classe 2E - L.S. “B. Varchi” - Montevarchi (AR)
a) [[…]]
b) Dal punto C [CD base minore del trapezio, AB base maggiore, CB lato obliquo maggiore] si conduce l’altezza CH, che è il dato che manca per calcolare l’area del trapezio.
Si dichiara l’incognita AH = x; di conseguenza è
BH = AB – AH = 12 – x.
Dato che è noto che BC = 15u, con il teorema di Pitagora si ricava CH:
CH = sqrt(15² - (12 - x )²) = sqrt(225 – 144 – x² + 24x) = sqrt(81 – x² + 24x)
Da D si conduce quindi l’altezza DK e risulta che AK = KH – AH = 8 – x, e dunque DK = sqrt(13² - ( 8 – x )²) = sqrt(169 – 64 – x² + 16x) = sqrt(105 – x² + 16x)
A questo punto possiamo calcolare la x:
sqrt(105 – x² + 16x) = sqrt(81 – x²
+ 24x)
105 – x² + 16x = 81 – x² + 24x
16x – 24x = 81 – 105
- 8x = - 24
x = 3 AH = 3u
AK = 8 – x = 8 – 3 = 5u
DH = CH = sqrt(169 – 25) = sqrt(144) = 12u
Adesso è possibile calcolare la superficie del trapezio:
A(ABCD) = ( 12 + 8 ) * 12 / 2 = 120 u²
c) [[…]]
[la costruzione, simile a quella della SM Dalla Chiesa, presenta alcune imprecisioni]
Soluzione proposta da:
Pierluigi Cameli, Giuseppe Cacciato e Giuseppe Petraia (classe 2E)
Pietro Di Giangi e Gaetano Di Venti, (classe 1C)
Liceo Scientifico “Farinato” - Enna (EN)
a) [[…]] [Calcoli corretti, non descritta la costruzione]
b) [[…]]
L’area del trapezio risulta essere allora:
(CD + AB) * AH / 2 = (12 u + 8 u) * 12 u / 2 = 120 u2
c) Il quadrato di area 120u2 deve avere
lato = u*sqrt(120). [[….]]
Il segmento di lato u*sqrt(120) si può ottenere come secondo cateto di un
triangolo rettangolo avente l’ipotenusa = 13u e un cateto = 7u. Per tracciare il
segmento:
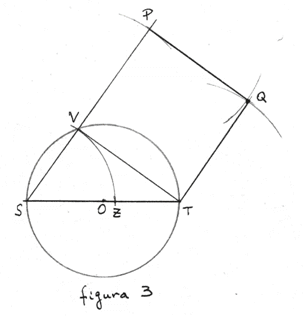
Consideriamo la circonferenza di centro O e diametro ST = 13u (figura 3).
Sul diametro ST prendiamo il punto Z tale che SZ = 7u. Con apertura di compasso
SZ e centro in S, tracciamo l’arco VZ. Il segmento VS è lungo 7u, l’angolo SVT è
retto perché inscritto in una semicirconferenza; VT è il lato del triangolo
cercato.
Per costruire il quadrato si prolunga il lato SV oltre V, puntando il compasso
in V si riporta su questo prolungamento un segmento VP = VT; mantenendo
invariata l’apertura del compasso e centrando nei punti P e T si tracciano i due
archi che si intersecano in Q; il quadrato PQTV è il quadrato richiesto.
| Home Page Cabri | Torna a FLATlandia | Archivi |