 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Novembre 2002
Il testo del problema:
Scelta a piacere una unità di misura OU,
rappresentata da +---+, e dati i tre segmenti
P+---+---+---+---+---+Q
R+---+---+---+S
T+---+---+---+---+---+---+---+V
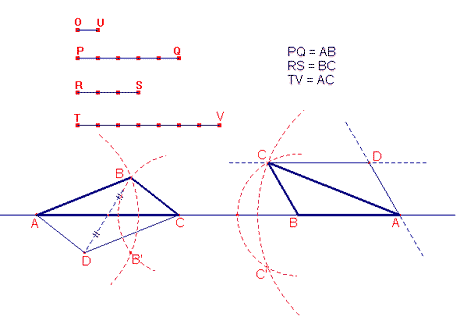
costruire il parallelogrammo ABCD in cui due lati
consecutivi misurino come PQ e RS, e una diagonale misuri come TV.
Sia I il punto medio del lato DC e K il punto in cui il segmento BI incontra
la diagonale AC.
a) Qual è il rapporto fra KC e AC?
b) In quale punto la retta DK incontra il lato CB?
Giustificare le risposte.
Commento
Ci sono giunte risposte da otto scuole, una di queste risposte con due soluzioni distinte e una con due diversi percorsi nel secondo quesito. Anche questa volta ha partecipato una sola scuola media, la stessa dello scorso mese. Si tratta di una caduta di interesse per la geometria? Speriamo di no.
Queste le scuole che hanno partecipato:
Nel problema proposto si assegnavano tre
segmenti costruiti a partire da una unità prefissata e si chiedeva di costruire
con essi un parallelogrammo, dati due lati e una diagonale. Seguivano poi due
quesiti che non dipendevano dai segmenti assegnati, ma dalle caratteristiche
generali dei parallelogrammi.
Lo scopo della costruzione era di invitare i ragazzi ad eseguire con precisione
la figura e ad indagare su eventuali diversi modi per ottenerla. Sono quindi da
considerarsi INCOMPLETE le risposte in cui non è stata illustrata la costruzione
richiesta.
Sono stati individuati due diversi modi per ottenere il parallelogrammo: o
utilizzando la caratteristica dei lati o ricorrendo alla proprietà delle
diagonali. Solo in una risposta è stata valutata la possibilità di ottenere più
figure, fra loro congruenti, ma con lo stesso tipo di costruzione.
Nelle dimostrazioni dei due quesiti
proposti sono stati seguiti diversi percorsi: chi ha utilizzato la similitudine
fra triangoli, chi la congruenza, chi ha fatto ricorso al teorema di Talete
(applicato al triangolo), chi ha usato la proprietà del baricentro.
Le giustificazioni sono in generale corrette e questo ci mette nell'imbarazzo
della scelta delle risposte da riportare all'attenzione di tutti i partecipanti.
Abbiamo riscontrato un solo errore di concetto (che segnaleremo alla classe
interessata), e alcune imprecisioni sulle quali riteniamo opportuno soffermarci:
Nelle costruzioni non è corretto riportare le "misure", le lunghezze si trasportano col compasso;
Le figure che si corrispondono nelle isometrie sono isometriche e quindi "congruenti" (sono anche equivalenti, ma non è vero il contrario: figure equivalenti NON SONO in generale congruenti);
Quando si chiede il rapporto fra due grandezze omogenee, la risposta corretta è un numero (nel nostro caso 1/3) e non la relazione che lega le due grandezze;
Tutte le affermazioni che discendono dalle ipotesi assegnate debbono essere giustificate, anche brevemente, e non basate sulla evidenza della figura.
Abbiamo stabilito di presentare le seguenti risposte:
SM "C. A. Dalla Chiesa", risposta completa in cui si fa ricorso alla similitudine in entrambi i quesiti (analogo percorso hanno seguito i ragazzi del LC "Beccaria" nella loro prima risposta);
LS "G. Galilei", risposta completa; in essa si fa ricorso al teorema di Talete come in quella del LC "Cavour";
LS "F. d'Assisi", risposta completa (dimostrazioni analoghe sono quelle del LST "Cesaris" e del LS "Leonardo (prima soluzione));
LS "Leonardo", a testimonianza dell'impegno dimostrato dalla classe, la parte a) della seconda soluzione, in quanto si differenzia dalle precedenti.
NOTA: come di consueto le correzioni o le osservazioni sono racchiuse in parentesi quadre; in doppia parentesi quadra si trovano invece le parti superflue o quelle omesse.
Soluzione proposta da:
Classe 3a P S.M.S. "C.A.
Dalla Chiesa"
San Genesio ed Uniti (PV)
a) Abbiamo costruito con Cabri i segmenti PQ, RS e
TV partendo da un segmento unitario mediante la simmetria centrale, nei rapporti
stabiliti dal testo del problema.
Mediante la funzione “trasporto di misura” abbiamo costruito il segmento BC
uguale a PQ e con la funzione “compasso” puntando rispettivamente in B e in C e
con aperture rispettivamente uguali a RS e TV abbiamo costruito il lato AB
consecutivo di BC e la diagonale AC del parallelogrammo.
Abbiamo trovato il quarto vertice tracciando la parallela a BC passante per A e
la parallela ad AB passante per C.
Preso il punto I come il punto medio di CD consideriamo i triangoli ABK e CIK:
[[ABK è uguale a CIK perché è il terzo angolo di due
triangoli con due angoli uguali.]]
Per questo motivo ABK e CKI sono triangoli simili e quindi hanno i lati in
proporzione:
CI è uguale a un mezzo di CD quindi CI è uguale a un mezzo di AB, allora CK è
uguale a un mezzo di AK e quindi CK = 1/3 AC [quindi il rapporto fra CK e AC è
1/3, vedi commento].
b) Chiamo F l’intersezione della retta DK con BC.
Considero i triangoli CKF e AKD:
[[ADK è uguale a KFC perché è il terzo angolo di due
triangoli con due angoli rispettivamente uguali]].
Per questo motivo AKD e FKC sono triangoli simili quindi hanno i lati in
proporzione.
Avendo dimostrato al punto a) che KC = 1/2 AK allora FC = 1/2 AD quindi F è il
punto medio del lato BC.
Soluzione proposta da:
Classe 2aB – Liceo Scientifico "E. Amaldi"
Bitetto (BA)
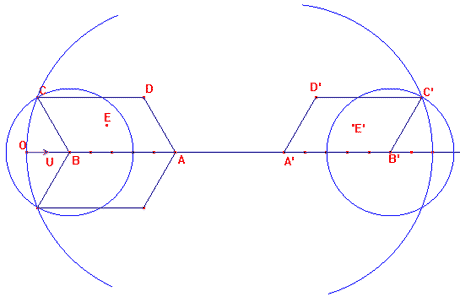
In riferimento alla figura, su una semiretta di origine O, prendiamo un punto U così OU=u (unità di misura) e costruiamo il simmetrico B di O rispetto ad U, di U rispetto a B, sino ad arrivare in A; evidentemente AB=5u.
Dopo disegniamo le circonferenze di centro B e raggio 3u, di centro A e raggio OA=7u; il punto di intersezione C è tale che BC=3u e AC=7u.
Costruiamo il punto medio E tra A e C ed il simmetrico D di B rispetto ad E: il quadrilatero ABCD è un parallelogramma avendo le diagonali che si dimezzano.
Ripetendo la costruzione (traslando in A’, altro punto
della semiretta, il vettore OU), ma con le circonferenze di centro A’ e raggio
7u, di centro B’ e raggio 3u, si costruisce l’altro parallelogramma possibile.
Quindi i parallelogrammi sono due, tra loro equivalenti [congruenti, vedi
commento], poiché il secondo equivale [è congruente] al simmetrico del primo,
rispetto alla retta della base: perciò ci riferiamo a quest’ultimo [in realtà si
ottengono quattro parallelogrammi, considerando anche il simmetrico del secondo
rispetto alla retta della base]
a) [[…]]
b) [[…]]
Soluzione proposta da:
Classe 2a E - Liceo Sciantifico “G.
Galilei”
Bitonto (BA)
Costruiti i segmenti OU, PQ, RS, TV come richiesto con le
funzioni compasso e simmetria centrale, abbiamo ottenuto il parallelogrammo ABCD
nel seguente modo:
tracciata una semiretta di origine A, abbiamo riportato su di essa con la
funzione compasso il segmento AB=PQ; sempre con la funzione compasso abbiamo
trovato il punto C come intersezione delle circonferenze di centro B e raggio RS
e di centro A e raggio TV; infine il punto D è stato individuato come punto di
intersezione delle rette per A parallela a BC e per C parallela ad AB.
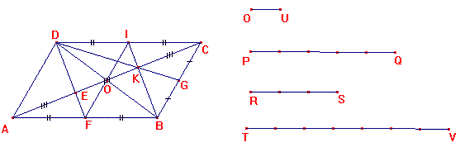
a) Detto I il punto medio del lato DC
e K il punto in cui il segmento BI incontra la diagonale AC,
abbiamo considerato il punto F medio del segmento AB e osservato che il
quadrilatero FBID è un parallelogramma avendo FB parallelo a DI e FB=DI per
costruzione; da ciò segue che DF è parallelo a IB. Sia E il punto intersezione
fra AC e DF.
Applicando il teorema di Talete alle rette
parallele DF e IB tagliate dalle trasversali DC e CA si ha che: essendo DI=IC
per costruzione, anche EK=KC;
applicando ancora il teorema di Talete alle stesse rette parallele tagliate da
CA e AB si ha che: essendo AF=FB per costruzione anche AE =EK;
Per transitività si ha pertanto che AE=EK=KC e quindi il rapporto tra KC e AC è 1/3.
b) Tracciate le diagonali DB e IF del parallelogrammo FBID, queste si incontrano nel punto O medio per ciascuna diagonale poiché in un parallelogrammo le diagonali si tagliano scambievolmente a metà, pertanto DO=OB.
Nel triangolo BCD, il segmento CO è la mediana relativa al lato BD, il segmento BI è la mediana relativa al lato DC e dunque K, loro punto d’incontro, risulta essere il baricentro del triangolo; ne consegue che la retta DK, passando per il baricentro contiene la terza mediana del triangolo e quindi va ad intersecare il lato CB nel suo punto medio G.
Soluzione proposta da:
Classe 2a D - Liceo
Scientifico “Francesco d’Assisi”
Roma
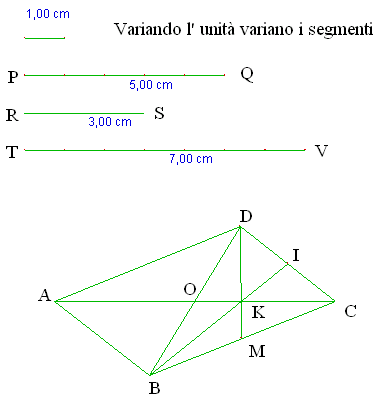
Creo la retta r
Con il trasporto di misura [procedura non corretta, vedi commento] riporto [su r] il segmento TV lungo 7u di estremi AC.
Con centro in A raggio PQ traccio la circonferenza C1; con centro in C e raggio RS traccio la circonferenza C2. IL punto di intersezione tra le circonferenze lo chiamo D.
Creo la semiretta d'origine D passante per O punto medio di AC. Applico una simmetria centrale di centro O per il punto D, trovando così il punto B: questo è il quarto punto del parallelogramma richiesto.
Ho applicato le proprietà dei parallelogrammi:
1) Ogni diagonale lo divide in due triangoli congruenti;
2) Il parallelogramma è un quadrilatero convesso dotato di un centro di
simmetria.
a) Considero il triangolo BCD: K è il suo
baricentro perché punto di incontro delle mediane IB e DM.
Sapendo che il baricentro divide ogni mediana in due parti tali che la parte
contenente il vertice è doppia dell'altra, si ha: KC=2OK. AO =~ OC per le
proprietà dei parallelogrammi. OC=3OK e quindi AC=6OK. Perciò KC/AC=2OK/6OK=1/3.
Quindi il rapporto tra KC e AC è 1/3.
b) La retta DK interseca il lato CB nel suo punto medio M perché K è il baricentro.
Soluzione proposta da:
Classe2a
F- Liceo Scientifico di Stato Sperimentale "Leonardo"
Brescia

| Home Page Cabri | Torna a FLATlandia | Archivi |