Soluzioni Maggio 2003

FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Maggio 2003

Il testo del problema:

a) Dato un qualunque triangolo ABC dividere il lato AB in due parti congruenti.
La circonferenza k di diametro AB incontra l'asse di AB in P.
La circonferenza k' di centro B e raggio BP interseca AB in Q.
Tracciata per Q la retta r parallela ad AC dimostrare che essa divide il triangolo ABC in due parti equiestese.

b) Estendere la costruzione in modo che il triangolo ABC risulti diviso in tre parti equiestese.

Giustificare la costruzione.

COMMENTO


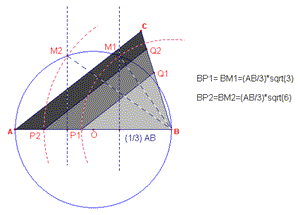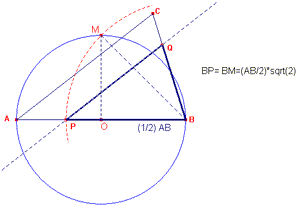
*Figura 1*	*Figura 2*

Avevamo lasciato aperto fino al 30 Settembre il termine per presentare la risoluzione del problema proposto nel mese di Maggio 2003. In esso si esponeva una costruzione per dividere un triangolo in due parti equivalenti mediante una linea parallela ad un lato.
Si chiedeva poi di estendere la costruzione in modo da dividere il triangolo in tre parti equivalenti. A Maggio abbiamo ricevuto risposte dalle scuole:

SM "Zanella", Roveredo in Piano (PN)
ITI "Berenini", Fidenza (PR)

I ragazzi dell'ITI "Berenini", che non avevano interpretato correttamente la seconda domanda, ci hanno inviato ora la costruzione richiesta.

Presentiamo quindi:

la risposta completa della classe 2^a A della SM "Zanella", che, coadiuvata probabilmente dall'insegnante, ha inviato un'esauriente e corretta risoluzione;
la seconda parte della risposta inviata dagli studenti Federica Rapaccioli e Matteo Galli, ora della classe 3^a BST dell'ITI "Berenini" (la prima parte, pur essendo corretta, è esposta in modo impreciso).

In entrambe le risposte non è stato però utilizzato, per risolvere la seconda parte del problema, il procedimento suggerito nel primo punto.
Nella seconda figura allegata al testo, viene da noi illustrato il percorso che permetterà di ottenere con una certa facilità la scomposizione di un triangolo in 3, 4, ...n parti equivalenti mediante segmenti paralleli ad un lato.
Basta dividere il lato AB in 3, 4, ...n parti congruenti e procedere come esposto nella prima parte del problema: tracciare la circonferenza di diametro AB, tracciare le perpendicolari ad AB nei punti di suddivisione, ...

NOTA: Il problema da noi proposto a Maggio è stato presentato in un caso particolare e poi generalizzato da un gruppo di insegnanti che hanno partecipato ad un seminario residenziale, “Progetto Eccellenza: matematica e software didattici”, tenutosi a Fiuggi nel 2001, organizzato dall'IRRE Lazio in collaborazione con l'IRRE Emilia-Romagna. (CLICCA QUI per scaricare il documento relativo in formato Acrobat)

Soluzione proposta da:
classe 2^a A - S.M. "Zanella" - Roveredo in Piano (PN)

1. Il triangolo PMB (M è il punto medio del segmento AB) è rettangolo isoscele per costruzione; se consideriamo MB come segmento unitario il segmento PB misura sqrt(2);

2. Il triangolo QBC’ è simile al triangolo ABC avendo gli angoli [[corrispondenti]] congruenti (consideriamo le rette per AC e QC’ parallele per costruzione e le rette per CB e AB: le coppie di angoli (dei triangoli QBC’ e ABC) di vertici C’ e C e Q e A sono congruenti perché corrispondenti; l'angolo di vertice B è in comune);

3. Se il segmento MB è unitario: il lato AB (triangolo ABC) misura 2 e il lato QB (corrispondente del [omologo di AB nel] triangolo QBR) misura sqrt(2) congruente con PB per costruzione (*); facendo il quadrato del loro rapporto (nelle figure simili il rapporto tra le aree è uguale al quadrato del rapporto delle misure lineari corrispondenti) troviamo che l' Area del triangolo QBC’ è la metà di quella del triangolo ABC quindi uguale a quella del poligono QC’CA.

* Si poteva anche considerare il triangolo ABP, rettangolo e isoscele per costruzione: se un cateto è segmento unitario l’ipotenusa AB misura sqrt(2) e il segmento QB misura 1. Consegue che il rapporto tra le aree dei triangoli (vedi sopra) è 2 a 1.

1. Retta r perpendicolare al segmento PB per P (passa per A, vedi considerazioni al punto precedente);
2. Circonferenza di centro P per M e sua intersezione R con r (BM, MP, PR sono segmenti unitari);
3. Segmento BR che misura sqrt(3) essendo BP di sqrt(2);
4. Circonferenze di centro B per P e per M e loro intersezioni S e T con BR;
5. Rette s e t parallele ad r per S e T, loro intersezioni con AB: A’, A’’.
6. Rette parallele al lato AC per A’’, A’ e loro intersezioni con BC: C’’, C’.

Per il Teorema di Talete i segmenti BA’’, BA’, BA sono in proporzione rispettivamente con 1, sqrt(2), sqrt(3);
le aree dei triangoli BA’’C’’, BA’C’’ BAC sono nei rapporti 1 a 2 a 3 quindi per differenza la aree dei quadrilateri AA’C’C, A’A’’C’’C’ sono uguali a quella del triangolo A’’BC’’.

Soluzione proposta da
Federica Rapaccioli e Matteo Galli
della classe 3^a BST - ITIS Berenini - Fidenza

Soluzione della seconda parte del problema

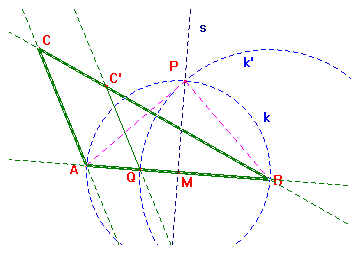
1) Si divide il segmento AB in tre parti congruenti mediante i punti M1 e M2 così determinati:

Si traccia un segmento AF con lunghezza arbitraria partendo dal punto A
Si traccia una circonferenza con centri in A e raggio arbitrario, l’intersezione tra la circonferenza e il segmento AF darà il punto M1’
Si traccia un’altra circonferenza con centro in M1’ raggio M1’A l’intersezione di quest’ultima circonferenza con il segmento AF darà il punto M2’
Con centro in M2’ e raggio M1’ M2’ si traccia un’altra circonferenza la quale interseca il segmento AF nel punto B’
Si traccia il segmento B B’
Si traccia la parallela a B B’ passante per il punto M2’ l’intersezione di questa con AB da il punto M2
Si traccia la parallela a B B’ passante per M1’ l’intersezione di questa con AB da il punto M1

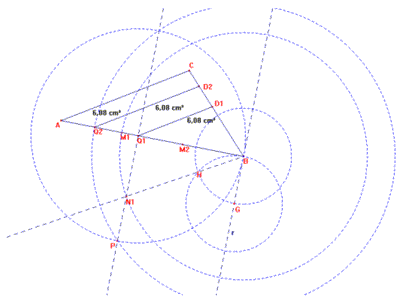
Divisione del triangolo in parti equivalenti:

2) Si traccia la circonferenza con centro B e raggio BM1
3) Si traccia la perpendicolare r ad AB passante per B
4) Si traccia una circonferenza con centro in B e raggio arbitrario che interseca r in G
5) Con centro in G e raggio BG che interseca la circonferenza del punto 4 in H
6) Si traccia la semiretta passante per B e H
7) L’intersezione tra la semiretta e la circonferenza del punto 2 darà il punto N1
8) Si traccia la perpendicolare ad AB passante per N1, tale retta interseca AB in Q1
9) Si traccia la parallela ad AC passante per Q1 che interseca CB in D1
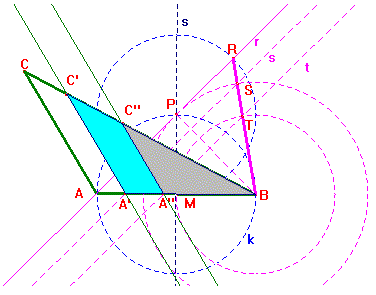
10) Si traccia la circonferenza di centro Q1 e raggio Q1B e la retta perpendicolare ad AB passante per Q1; la loro intersezione è il punto P
11) Si traccia la circonferenza di centro B e raggio BP che interseca AB in Q2
12) Si traccia la parallela ad AC passante per Q2 che interseca CB in D2
13) Si osserva che il quadrilatero AQ2D2C, il quadrilatero Q2Q1D1D2 e il triangolo Q1BD1 sono equivalenti.

Giustificazione:
Q1B è stato costruito come altezza di un triangolo equilatero di lato M1B che è i 2/3 di AB pertanto

Q1B = (sqr(3) / 2) * M1B = (sqr(3) / 3) AB

Pertanto, essendo il rapporto fra le aree di triangoli simili uguale al quadrato del rapporto tra lati omologhi, ed essendo il triangolo Q1BD1 simile al triangolo ABC, l’area del triangolo Q1BD1 è 1/3 dell’area del triangolo ABC

Q2B è stata costruita come diagonale del quadrato di lato Q1B pertanto

Q2B = sqr(2) * Q1B

Pertanto essendo il triangolo Q2BD2 simile al triangolo Q1BD1, l’area del triangolo Q2BD2 è il doppio dell’area del triangolo Q1BD1

Per differenza l’area del quadrilatero Q2Q1D1D2 è 1/3 dell’area del triangolo ABC e Infine ancora per differenza l’area del quadrilatero AQ2D2C è 1/3 dell’area di ABC.

| Home Page Cabri | Torna a FLATlandia | Archivi |