FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)

Gennaio 2003

Il testo del problema:

1. Data una corona circolare, costruire il diametro di un cerchio avente la stessa area della corona.
    
2. Determinare due cerchi concentrici tali che l'area della corona circolare da essi individuata sia uguale all'area del cerchio di raggio minore.

Giustificare le risposte.

Commento

Abbiamo ricevuto dodici risposte, di cui tre provengono da scuole medie e cinque da una stessa scuola superiore (un gruppo di tre allievi di una classe prima e risposte singole o a coppie di allievi di una classe seconda). Siamo compiaciuti per tale partecipazione, anche se alcune di quelle risposte necessitavano di una maggior riflessione.

Queste sono le scuole che hanno partecipato:

• SM "G. B. Tiepolo", Milano (MI)
• Scuola Media, Ist. Compr. di Venasca (CN)
• SM "C. A. Dalla Chiesa", S. Genesio ed Uniti (PV)
• LS "E. Amaldi", Bitetto (BA)
• LS "G. Galilei", Bitonto (BA)
• ITI "Berenini", Fidenza (PA) - cinque risposte
• LS "G. Verdi", Valdobbiadene (TV)
• LS "G. Galilei, Adria (RO)

Il problema di questo mese aveva come argomento la corona circolare e proponeva due costruzioni, di cui la seconda era un caso particolare della prima. In due risposte non è stata eseguita la seconda costruzione; nelle altre, dove sono state individuate entrambe, non sempre sono state giustificate in modo esauriente. Come abbiamo detto più volte, poiché gli anni passano e i ragazzi cambiano, ripetiamo ancora che lo scopo della risoluzione di un problema non è solo trovare il risultato, ma saper giustificare in modo chiaro e completo il proprio operato, anche nei casi più evidenti. Ripetiamo inoltre che saremo più esigenti con i ragazzi del biennio che con quelli della scuola media inferiore.

Il problema non si prestava a molte interpretazioni, ma si sono evidenziati ugualmente due diversi percorsi nella risposta al primo punto, mentre nel secondo punto nessuno è giunto alla conclusione che la corona circolare richiesta fosse formata dalle circonferenze inscritta e circoscritta ad un quadrato.
L’esposizione è in generale corretta, tuttavia ci sembra opportuno fare alcune precisazioni:

• Col termine congruente si indica la “sovrapponibilità” di due grandezze omogenee (coppie di segmenti, di triangoli, di archi,…); la lunghezza, l’area, il volume sono misure e si dovrà dire, ad esempio, che l’area della figura F è uguale all’area della figura F’ qualora le due aree siano rappresentate dallo stesso numero rispetto alla stessa unità di misura.

• La corona circolare e il cerchio sono porzioni di piano di cui si può calcolare l’area; la circonferenza è una linea curva di cui si può calcolare la lunghezza

Le risposte accolte sono sette ma non le presenteremo tutte. Abbiamo scelto le seguenti soluzioni:

Per le scuole medie

• Scuola Media di Venasca, la prima parte.
• SM “C. A. Dalla Chiesa”, la seconda parte.

Per le scuole superiori

• LS “G. Galilei” di Bitonto, risposta completa.
• LS “E. Amaldi”, risposta completa; nella parte a) si fa ricorso alla stessa proprietà utilizzata dai ragazzi del LS Galilei di Bitonto, ma si procede in modo diverso nella costruzione.
• LS “G. Verdi”, la prima parte.
• ITI LST “Berenini”, classe 1Bst, la seconda parte.

Segnaliamo inoltre la soluzione di Federica Rapaccioli e Alessandro Manfredi della classe 2Bst del Berenini, analoga alle due parti citate sopra.

NOTA: come di consueto le correzioni o le osservazioni sono racchiuse in parentesi quadra; in doppia parentesi quadra si trovano invece le parti superflue o quelle omesse.

Soluzione proposta da
Classe 2^a B - Scuola Media dell’Ist. Comprensivo Venasca (CN)

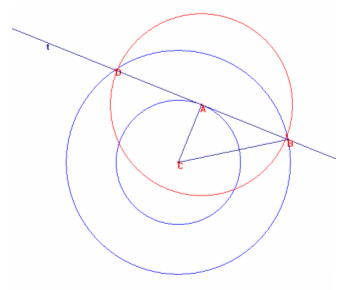
1) Data una circonferenza di raggio r [CA nella figura 1], si costruisca la tangente [t] in A alla circonferenza[tracciando la retta perpendicolare in A al raggio AC]; costruita una seconda circonferenza concentrica con la prima e di raggio maggiore, R, si determinino le intersezioni della seconda circonferenza con la retta tangente t individuando i punti B e D.
Il segmento CB risulta essere, ovviamente, il raggio R della seconda circonferenza e, poiché l’area della corona circolare è data da 3,14(R^2 – r^2), considerando che il triangolo ACB è rettangolo con ipotenusa CB (=R) e cateto CA (=r), il cateto AB risulterà essere il raggio di un cerchio avente la stessa area della corona circolare.

Pertanto la corda BD sarà il diametro del cerchio richiesto.

2) [[…]]

Soluzione proposta da
Classe 3^a P - S.M. “C. A. Dalla Chiesa” - San Genesio ed Uniti (PV)

1) [...]

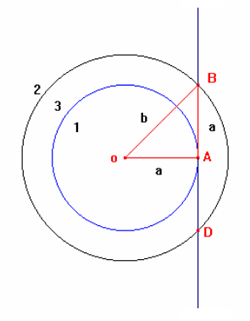
2) Costruiamo una circonferenza C1 di centro O e tracciamo il raggio OA di misura “a” e la tangente a C1 nel punto A; con il compasso, puntando in A, riportiamo la misura di “a” sulla retta tangente e chiamiamo B l’intersezione.
Il triangolo OAB è un triangolo rettangolo avente i cateti uguali [[…]].

[Tracciamo la circonferenza C2 di raggio OB].

Poiché prima abbiamo dimostrato che la corona circolare ha la stessa superficie di un cerchio avente il raggio uguale al cateto AB, in questo caso AB=AO=a e perciò ha la stessa area di C1.

Soluzione proposta da
Classe 2^a E - Liceo scientifico “G. Galilei” - Bitonto (BA)

1) Sia r=EF il raggio del cerchio c e r’=EG il raggio circonferenza della c’ , con r’<r.
L’area della corona circolare individuata da c e c’ misura A” = A-A’ = r²- r’² = (r² - r’²), pertanto il raggio R del cerchio c” di area pari a quella della corona circolare sarà tale che

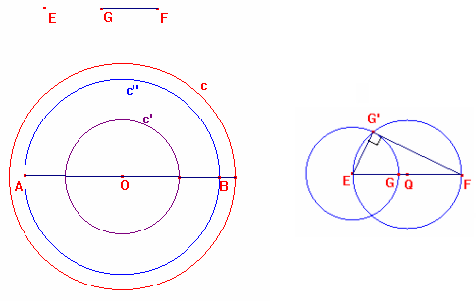
R²= r² – r’² e quindi R =. Questo risultato ci dice che R è il cateto di un triangolo rettan-golo di ipotenusa r e cateto r’. A tal proposito basta tracciare la circonferenza di diametro EF, quella di raggio EG e, detto G’ uno dei loro punti intersezione, G’F sarà il raggio R richiesto.
Puntando nello stesso centro O di c e c’, tracciamo la circonferenza c” di raggio R=G’F e quindi il suo diametro AB=2R.

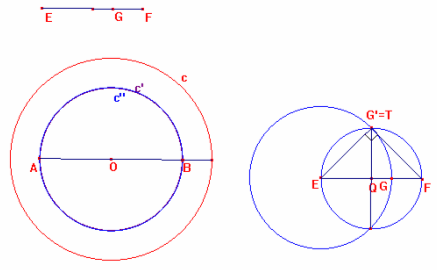
2) Se in particolare si vuole che l’area della corona circolare sia uguale a quella del cerchio di rag-gio minore, si deve avere che:

(r² - r’²) = r’² => r² -r’² = r’² => 2r’² = r² ed infine r’² = r²/2 , relazione che intercorre fra il ca-teto e l’ipotenusa di un triangolo rettangolo isoscele.
A questo punto basta costruire il triangolo rettangolo isoscele di ipotenusa EF (basta tracciare il diametro perpendicolare ad EF nella circonferen-za di diametro EF, per avere ET nella relazione cercata con EF). [[…]] [Poiché T=G’] allora c”=c’.

Pertanto la circonferenza di raggio		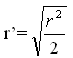divide il cerchio di raggio r, ad esso concentrico,
in due parti equivalenti.

Soluzione proposta da
Classe 2^a B - Liceo Scientifico "E. Amaldi" - Bitetto (BA)

In riferimento alle figure allegate:

a) Se la circonferenza esterna ha raggio OB=R e quella interna concentrica ha raggio OA=r, l'area della corona circolare è pi*(R^2-r^2), dove pi è il “p”greco.

Fissato il punto medio O' del segmento OB, se C è una intersezione della circonferenza di centro O' e raggio OO'=O'B con la circonferenza interna di raggio r=OA=OC, il segmento BC risulta tangente alla circonferenza interna e perpendicolare al raggio r=OC nel punto di tangenza C (l'angolo OCB è 90° perché inscritto in una semicirconferenza).

Essendo quindi OB=R, OC=OA=r e angolo OCB=90°, per il teorema di Pitagora sarà BC^2=R^2-r^2 e la circonferenza [il cerchio] di raggio BC avrà area pi*(R^2-r^2) come quella della corona circolare.
Infine, se D è il punto diametralmente opposto a B nell'ultima circonferenza, il segmento BD è il diametro richiesto.

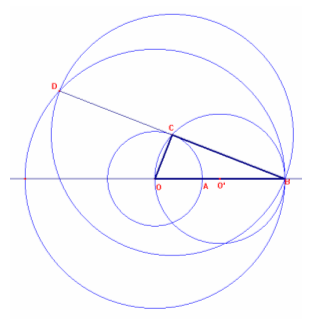
b) Data la circonferenza di raggio OA=r, costruito un quadrato su OA e di lato OA=r, la sua diagonale OC è r*rad(2).

Pertanto la circonferenza ad essa concentrica e di raggio R=OC=r*rad(2)=OB è tale che l'area della corona circolare è pi*(R^2-r^2)=pi*(2r^2-r^2)=pi*r^2, [quindi uguale all’] area della circonferenza [cerchio] interna.

Soluzione proposta da
Elisabetta Andreola, Silvia Piazza e Monica Verri
Classe 2ªA – Liceo scientifico “G. Verdi” - Valdobbiadene – TV

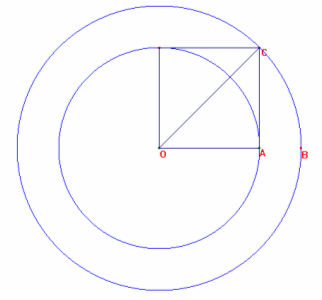
1)
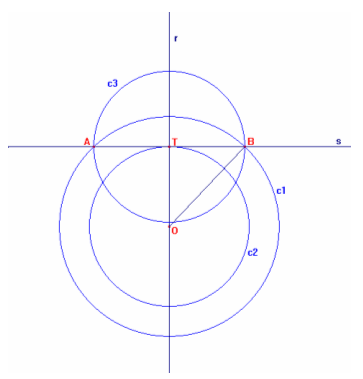
Disegno le circonferenze concentriche c1 e c2 (c2 di raggio minore) di centro O , che individuano una corona circolare.
Traccio per il punto O una retta r e chiamo T un suo punto d’intersezione con la circonferenza c2. Per T traccio la retta s perpendicolare alla retta r ed indico con A e B i punti d’intersezione di s con la circonferenza c1.
Poiché il triangolo OTB è rettangolo, per il teorema di Pitagora , si ha:
a) TB²=OB²-OT²
Dall’uguaglianza a), moltiplicando ciascun termine per , si ottiene l’uguaglianza b):
b) TB²=OB²-OT²
Il secondo membro dell’uguaglianza b) rappresenta l’area della corona circolare data, che è perciò equivalente all’area del cerchio delimitato dalla circonferenza c3 di raggio TB.
AB è una corda della circonferenza c1, perpendicolare ad r. Segue che la retta r divide la corda AB in due parti uguali (TA=TB) ed, essendo TB il raggio della circonferenza c3, AB ne è il diametro.

2) [[…]]

Soluzione proposta da
Classe 1B st - ITI “Berenini” - Fidenza (PR)

1) [...]

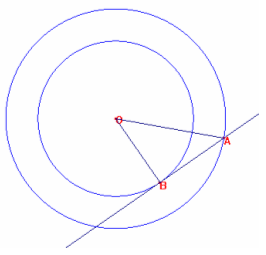
2) Data la circonferenza di raggio minore, disegnare il raggio (OB), trovare la retta perpendicolare a quest’ultimo nel punto B, riportare da B la misura del raggio sulla retta trovando A. Unendo il centro della circonferenza con il punto trovato sulla retta, si trova un triangolo rettangolo isoscele OAB i cui cateti sono congruenti al raggio.

L’ipotenusa OA risulta essere il raggio del cerchio concentrico a quello di partenza e che forma con esso una corona circolare la cui area è uguale all’area del cerchio di raggio minore. Infatti applicando ancora il teorema di Pitagora nel triangolo rettangolo isoscele OAB si ha: OB² = OA² - OB² quindi come nel punto precedente moltiplicando per si ottiene l’uguaglianza tra le aree richieste.

| Home Page Cabri | Torna a FLATlandia | Archivi |