 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo è vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo è vasto e
largo". (Edwin A. Abbott)
Febbraio 2003
Il testo del problema:
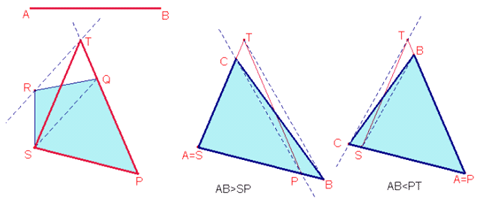
Dato un quadrilatero qualsiasi SPQR ed un segmento AB, trasformare il quadrilatero in un triangolo ABC ad esso equivalente.
Giustificare la costruzione.
Commento
Ci sono giunte sette risposte provenienti da sei scuole (due medie inferiori e quattro superiori). Abbiamo inoltre ricevuto altre risposte da almeno due mittenti, ma abbiamo dovuto eliminarle perché contenenti virus.
Le scuole che hanno inviato risposte sono:
Il problema proposto per questo mese aveva
come argomento l'equivalenza piana, forse non tutti i ragazzi che seguono
FLATlandia hanno già trattato questo tema a scuola.
Si chiedeva di trasformare un quadrilatero in un triangolo equiesteso avente un
lato già assegnato.
Il procedimento ottimale era quello di trasformare il quadrilatero in un
triangolo equivalente e, dopo aver sovrapposto il segmento dato su uno dei lati
del triangolo ottenuto, eseguire ancora una trasformazione con una costruzione
analoga alla precedente.
Solo in tre delle risposte giunte è stato seguito questo percorso, ma in nessuna
di esse sono state esplorate tutte le possibilità che potevano presentarsi: il
segmento dato poteva essere minore, maggiore o banalmente uguale a un lato del
triangolo ottenuto dalla prima trasformazione.
Il metodo di risoluzione era comunque lo stesso.
In due risposte sono stati seguiti percorsi diversi da quello prima citato. Una,
in particolare, in cui sono stati operati nella seconda trasformazione due
successivi passaggi basati sul secondo teorema di Euclide, è stata considerata
corretta, ma eccessivamente laboriosa.
Nelle rimanenti è stato esaminato solo un caso particolare.
Per le scuole superiori è stata scelta la
soluzione del
LS "Leonardo", analoga a quelle inviate da LS "G. Galilei" e da Santi Luca dell'ITI
"Berenini".
A testimonianza dell'impegno dimostrato vengono presentate entrambe le soluzioni proposte dalle due scuole medie inferiori, anche se una presenta solo un caso particolare e l'altra basa la sua costruzione su un calcolo algebrico.
NOTA: come di consueto le correzioni o le osservazioni sono racchiuse in parentesi quadra; in doppia parentesi quadra si trovano invece le parti superflue o quelle omesse.
Soluzione proposta da
Classe 2a F - Liceo Scientifico
Sperimentale “Leonardo” - Brescia (BS)
Fig.1 [accanto al quadrilatero si doveva tracciare anche il segmento AB prescelto]
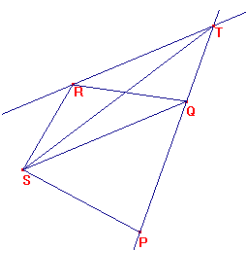
Dato il quadrilatero SPQR traccio la diagonale SQ e la sua
parallela passante per R, indico con T il punto di intersezione tra tale
parallela e il prolungamento del lato PQ.
Il triangolo SPT è equivalente al quadrilatero SPQR in quanto somma di triangoli
equivalenti: entrambi sono composti dallo stesso triangolo SPQ e dai due
triangoli SRQ e SQT equivalenti tra loro perché aventi la stessa base SQ e
la stessa altezza [altezze congruenti] (la distanza fra le due rette parallele).
Fig.2
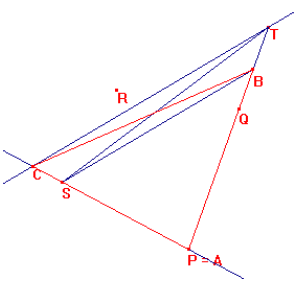
Ora si tratta di trasformare il triangolo SPT in un altro equivalente avente per lato il segmento assegnato AB:
Sulla base PT del triangolo così ottenuto riporto AB in
modo che A coincida con P. Unisco S con B e traccio la parallela a SB passante
per T, indico con C il punto di intersezione tra tale parallele e la retta AS (C
sarà interno al lato PS se B è esterno al lato PT).
Il triangolo ABC così ottenuto è equivalente al triangolo SPT perché somme di
triangoli equivalenti. [affermazione da giustificare come fatto nella prima
parte]
Per la proprietà transitiva dell’equivalenza tra poligoni SPQR è equivalente al
triangolo ABC.
Soluzione proposta da:
Valeria Cua, Andrea Maida, Marco Zetti, Marta Zuffi
Classe 3a P della Scuola Media “C.A.
Dalla Chiesa” di S.Genesio ed Uniti (PV).
Abbiamo risolto parzialmente il problema, cioè solo nel caso cui AB è congruente alla diagonale PR del quadrilatero SPQR; [[…]].
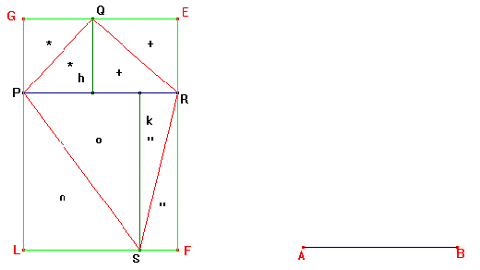
Abbiamo considerato il quadrilatero SPQR e
abbiamo tracciato due rette parallele alla diagonale PR passanti per Q ed S, e
due rette perpendicolari alle precedenti passanti per R e P.
Individuiamo i punti d’incontro delle rette tracciate e otteniamo così un
rettangolo GEFL circoscritto al quadrilatero SPQR.
Il rettangolo ha una superficie doppia del quadrilatero come evidenziato nel
disegno allegato.
Poiché una dimensione del rettangolo è uguale al segmento dato AB, considero il
triangolo di vertici LFC, dove C è un punto qualunque del lato GE.
Questo triangolo avente una superficie che è la metà del rettangolo GEFL è
equiesteso al quadrilatero SPQR.
Soluzione proposta da
Classe 2a B - Scuola Media “L. da
Vinci” - Rufina (FI)
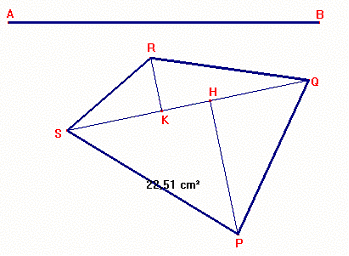
Abbiamo considerato il quadrilatero SPQR costituito dai
due triangoli SPQ e SQR con la base SQ in comune.
Abbiamo inoltre costruito le altezze di tali triangoli, PH ed RK, relativamente
alla base SQ.
Quindi l’area del quadrilatero SPQR può essere considerata come risultato della
somma delle aree dei due triangoli SQR e SQP.
A(SPQR) = A(SQP) + A(SQR)
A(SQP) = (SQ * PH) /2 A(SQR) = (SQ * RK) /2
A(SPQR) = (SQ * PH) /2 + (SQ * RK) /2 e, mettendo in evidenza
A(SPQR) = SQ * (PH + RK) * 1/2
Abbiamo costruito il triangolo ADE avente la base AD congruente alla diagonale SQ e l’altezza EH’ congruente alla somma delle altezze RK e PH [anche se si tratta di una costruzione semplice, sarebbe stato corretto indicare un procedimento (geometrico) per ottenere tale somma].
Quindi
A(SPQR)=A(ADE)
Per trasformare il triangolo ADE in un altro equivalente di base qualsiasi abbiamo seguito il seguente procedimento:
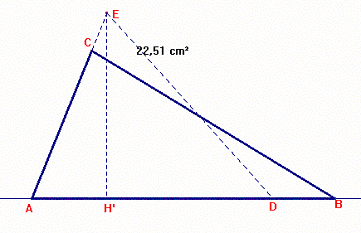
sulla retta r [[…]] [riportiamo il segmento AB (vedi
figura)]. Uniamo il vertice E con il punto B e tracciamo la parallela al
segmento BE passante per il vertice D.
Tale parallela interseca la retta AE nel punto C.
Il triangolo ADE è così composto dai due triangoli ADC e CDE.
Il triangolo CDB, è equivalente al triangolo CDE perché aventi base in comune CD
e altezza congruente alla distanza del segmento BE con la sua parallela CD.
Il triangolo ABC, di base qualunque AB risulta quindi equivalente al triangolo ADE perché equicomposto con esso (ADC in comune e CDB equivalente CDE), e di conseguenza equivalente al quadrilatero dato SPQR.
[[…]]
| Home Page Cabri | Torna a FLATlandia | Archivi |