 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Dicembre 2002
Il testo del problema:
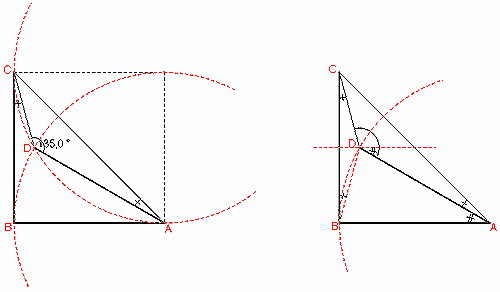
E’ dato un triangolo rettangolo isoscele ABC, di ipotenusa AC.
a) Individuare mediante una costruzione un punto D interno al triangolo, tale che sia DC = BC = BA e l’angolo DCB congruente all’angolo DAC
b) Determinare in tal caso la misura di ciascun angolo del triangolo CAD.
Commento
Abbiamo ricevuto dieci risposte, di cui due provengono da scuole medie inferiori. Alcuni ragazzi partecipano per la prima volta a FLATlandia e, nel caso che non abbiano avuto successo, li invitiamo a non desistere e auguriamo loro un esito più soddisfacente con i prossimi problemi.
Le scuole che hanno partecipato sono:
Nel problema proposto per il mese di Dicembre si chiedeva
di costruire un punto, all'interno di un triangolo rettangolo isoscele, che
soddisfacesse a due particolari condizioni. Sono stati individuati due diversi
modi per ottenere tale punto: intersecando due opportune circonferenze oppure
intersecando una determinata circonferenza con l'asse di un cateto.
Chi ha individuato la prima costruzione ha utilizzato, anche se in modo
inconsapevole, la nozione di arco capace di un dato angolo (cioè tale che tutti
gli angoli in esso inscritti sono congruenti all'angolo dato) ed ha saputo, in
generale, giustificare il proprio operato.
Quelli che hanno invece proposto la seconda costruzione non hanno, nella maggior
parte, saputo giustificarla oppure lo hanno fatto in modo non soddisfacente.
Ricordiamo ancora che le caratteristiche che vengono scoperte indagando su una
figura con il software Cabri, debbono poi essere dimostrate.
Abbiamo stabilito di presentare le seguenti risposte, complete dalle rispettive figure:
NOTA: come di consueto le correzioni o le osservazioni sono racchiuse in parentesi quadra; in doppia parentesi quadra si trovano invece le parti superflue o quelle omesse.
Soluzione proposta dalla Classe 2a
B
Liceo Scientifico "E. Amaldi" - Bitetto (BA)
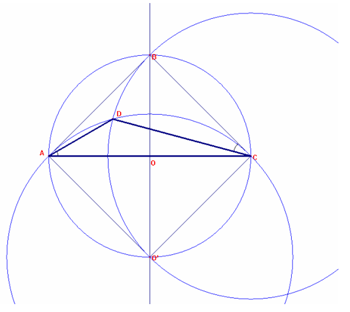
In riferimento alla figura sopra, dato il segmento AC, disegniamo il suo asse e la circonferenza con centro nel punto medio O, di raggio OA. Dette B, O' le intersezioni asse-circonferenza, AC e BO' sono due diametri perpendicolari, per cui otteniamo il triangolo ABC rettangolo isoscele, essendo inscritto in una semicirconferenza ed essendo B sull'asse (lo è anche AO'C con angoloBCO' = 90°).
a) Intersecando la circonferenza di centro C e raggio CB con quella di centro O' e raggio O'C=O'A, otteniamo il punto richiesto D [[...]].
Infatti è DC = BC = AB e [nella circonferenza di centro O'] l'angolo BCD (con lato BC tangente, essendo BO' raggio e BCO' = 90°, e lato CD corda-secante [corda CD lato-secante] ) è corrispondente [congruente] dell'angolo DAC poiché insistono sullo stesso arco DC.
b) Essendo angolo AO'C = 90°, il suo esplementare, concavo, misura 270° e l'angolo ADC alla circonferenza che insiste sullo stesso arco AC [[...]], misura 270°/2 = 135°. Inoltre il triangolo O'CD è equilatero (O'C = O'D perché raggi di una stessa circonferenza e O'C = BC = CD essendo anche [il triangolo] BCO' rettangolo isoscele). Quindi angoloDCA = angoloDCO' - angoloACO' = 60°-45° = 15°. L'angolo DAC misura, infine, 180°-135°-15° = 30°.
Soluzione proposta da Eleonora Bazzo,
classe 1a
D
Liceo Classico "C. Cavour" - Torino (TO)
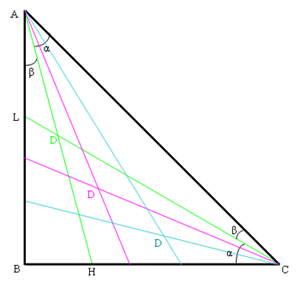
[Nel triangolo rettangolo isoscele ABC, di ipotenusa AC,] si tracci:
Dall’angolo BAC si nota che
alfa+beta
= 45°. Perciò, dal
triangolo ADC, [si ricava che] l’angolo in D =135°.
Cambiando i valori di
alfa (e quindi di
beta), si otterrebbero i punti D’ e D": anche
in questi casi l’angolo in D è sempre uguale a 135°. Si è di fronte ad una serie
di angoli alla circonferenza che insistono sullo stesso arco AC, che appartiene
ad una circonferenza il cui centro è sull’asse del lato AC; il centro è anche
equidistante dai punti D, D’, D" e da A e C. Unendo quattro di questi punti a
due a due, si individuano due segmenti i cui assi si incrociano nel centro della
circonferenza in questione [E].
L’arco di questa circonferenza, quindi, è il luogo dei punti individuati dal
punto D al variare di
alfa (e quindi di
beta).
Il punto D [...], perciò, si individua con l’intersezione dell’arco di
circonferenza AC (con centro in E) con quello di BE (con centro in C [[...]]);
entrambi hanno raggio BC.
[Non viene né qui né in seguito rilevato che il centro E è vertice del quadrato di lati AB e BC in quanto all'angolo alla circonferenza di 135° corrisponde un angolo al centro di 270°. Questa mancanza pregiudicherà la correttezza delle successive conclusioni.]
[[...]]
Soluzione proposta da Valeria Cua,
Andrea Maida, Marco Zetti, classe 3a
P
Scuola Media "C.A. Dalla Chiesa" - San Genesio ed Uniti (PV)
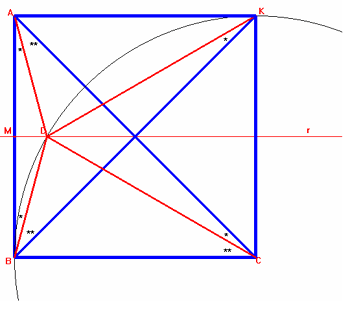
a)
Costruiamo il triangolo [rettangolo] isoscele ABC di ipotenusa AC.
Disegniamo la circonferenza con centro in C e apertura CB, prendiamo il punto
medio di AB e tracciamo la retta "r" parallela a BC passante per esso.
Chiamiamo D il punto di intersezione con la circonferenza, interno al triangolo.
Congiungiamo D con i punti A, C e B.
Costruiamo il simmetrico di ABC rispetto al lato AC e chiamiamo K il simmetrico
di B [essendo anche il triangolo AKC rettangolo e isoscele di ipotenusa AC, il
punto K è vertice del quadrato di lati BC e CA e si trova sulla circonferenza di
centro C e raggio BC]; uniamo K con B. L'angolo BCD è il doppio dell'angolo BKD
perché [[...]] [rispettivamente angolo al centro e angolo alla circonferenza]
che insistono su uno stesso arco, BD.
Chiamiamo "a" l'ampiezza di BKD e "2a" l'ampiezza di BCD.
La retta "r" [[...]], passante per D [,essendo perpendicolare al lato AB] è asse
di simmetria del quadrato [ABCK] e quindi possiamo dire [[...]] che i triangoli
BDK e ADC sono congruenti [essendo B, A e C, K coppie di punti corrispondenti]
di conseguenza gli angoli DCA e DKB sono uguali.
Il triangolo ADB è isoscele perché "r" è l'asse del segmento AB e D si trova
sull'asse: quindi ABD = BAD per costruzione.
Consideriamo il triangolo BCD, isoscele per costruzione:
CBD = (180°-2a)/2 = 90°-a quindi ABD = BAD = a
Poiché DAC = 45°-a, avrà ampiezza uguale a DCB.
b)
[[...]]
| Home Page Cabri | Torna a FLATlandia | Archivi |