FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Ottobre 2001

Il testo del problema:

Siano r ed s due rette incidenti in O e sia P un punto non appartenente ad esse.

a) Costruire un punto A su r ed un punto B su s in modo che il segmento AB abbia P come punto medio.
b) Come deve essere preso il punto P affinché la retta OP sia asse di AB?

Motivare le risposte.

Commento

Care ragazze, cari ragazzi,
abbiamo ricevuto diciotto risposte, una delle quali però non è leggibile causa una errata procedura di spedizione. Sette provengono da scuole medie inferiori e una di queste, come nell'Ottobre dello scorso anno, ci è giunta da Rosario in Argentina.
Anche se le soluzioni inviate non sono tutte valide ci fa piacere riscontrare questo interesse per le questioni di geometria. A chi non ha avuto successo suggeriamo di riprovare!

Le scuole che hanno partecipato sono:

• SM "Panzacchi" Ozzano BO
• SM "Jussi " S. Lazzaro di Savena BO
• SM "Dante Alighieri" Rosario Santa Fe - Argentina
• Scuola Media di San Genesio PV
• SM "De Amicis" (citta'??)
• SM "Zanella" Roveredo in Piano PN
• SM "L. da Vinci" Rufina FI
• LS "E. Boggio Lera" Catania CT (due risposte)
• LS "G.Galilei" Bitonto BA
• ITI "G. Giorgi" Milano MI
• LS "Giorgione" Castelfranco Veneto TV
• LS "F. Buonarroti" Pisa PI
• LS "E. Amaldi" Bitetto BA
• LS "G. Galilei" Adria RO (due risposte)
• LST "B. Pascal" Merano BZ
• LS "E. Majorana" Guidonia RM

Nel problema proposto per il mese di Ottobre si chiedeva di costruire un segmento, con gli estremi vincolati su due rette incidenti, essendo assegnato il suo punto medio e di esaminare poi una situazione particolare.
La risoluzione non presentava eccessive difficoltà ed è stata affrontata in vari modi: c'è chi ha fatto ricorso alla simmetria centrale e/o a quella assiale, chi ha utilizzato le proprietà del parallelogramma e chi il teorema di Talete (o la similitudine).
Un gruppo di scuola media ha proposto una costruzione basata sulla proprietà del baricentro, corretta, ma giudicata eccessivamente laboriosa.
Alcune risposte, come abbiamo già detto, sono state considerate non accettabili o per incompletezza o per notevoli imprecisioni di procedimento; alcune altre, pur avendo positivamente risolto la costruzione, presentano errori o carenze nelle motivazioni e/o nelle descrizioni del procedimento.
Fra le risposte giudicate valide, presenteremo le parti più significative per semplicità nella costruzione e/o per chiarezza nella esposizione, in modo da proporre vari modi di risoluzione.
Riteniamo sia opportuno fare prima alcune osservazioni:

• chi usa un software di geometria per indagare il problema, non può ritenere valida come costruzione una figura ottenuta per successivi aggiustamenti; per COSTRUZIONE si può intendere un insieme di "passaggi" che permettono di ottenere una figura che non perda le sue caratteristiche se si modificano i suoi elementi base;
• chi non ha risolto la prima parte, per risolvere la seconda deve comunque costruire la figura;
• due rette incidenti formano quattro angoli bisecati da due rette bisettrici;
• se AB è diagonale di un parallelogramma, occorre motivare il fatto che, nella nostra costruzione, P appartenga ad essa;
• se A (o B) appartiene ad una retta, è opportuno precisare che il suo corrispondente, in una qualsiasi trasformazione, appartiene alla retta corrispondente;
• per poter applicare il Teorema di Talete, occorrono almeno tre rette parallele.

Per le scuole superiori riportiamo le seguenti risposte:

• La soluzione della classe 2B - LS "E. Amaldi"
• La soluzione della classe 2C - LS "Giorgione" (una costruzione simile, ma incompleta, è stata proposta da un ragazzo del LST "B. Pascal")
• La parte a), secondo modo, della classe 2E - LS "G. Galilei" di Bitonto
• La soluzione della classe 3D - LS "F. Buonarroti" (una risposta analoga, ma confusa nella esposizione, è quella inviata da un gruppo della 3D - SM "De Amicis")

Per le scuole medie inferiori, riportiamo:

• La parte a) della classe 3P - SM di San Genesio
• La parte b) della classe 2A - SM "D. Alighieri" di Rosario
• La parte b) secondo modo, della SM di Rufina
• La soluzione della SM "Zanella"

NOTA 1: Le correzioni al testo o i commenti sono scritti in parentesi quadra. Sono racchiuse in doppia parentesi quadra le parti ritenute superflue.

NOTA 2: Non tutti i componenti del gruppo di FLATlandia ricevono i file Cabri. Quindi NON INVIATE IL TESTO in questo formato, ma SOLO LE FIGURE.

Soluzione proposta da:
Classe 2^a B - Liceo Scientifico Statale "E.Amaldi" - Bitetto (BA)

a) Date le 2 rette r, s incidenti in un punto [O, e un punto] P non appartenente ad esse, costruiamo il simmetrico O' di O rispetto a P (così P diventa punto medio del segmento OO').
Da tale punto O' mandiamo le parallele alle due rette r,s che le intersecano nei punti A, B richiesti (vedi 1ª fig.). Infatti nel parallelogramma O'AOB la diagonale AB dimezza l'altra diagonale proprio nel punto P (unicità del punto medio). Quindi P risulta medio di AB.

b) Prendendo il punto P sulla bisettrice b di [uno degli] angoli formati dalle due rette r,s il parallelogramma diventa un rombo (vedi 2ªfigura). Infatti il triangolo OAO' è isoscele (angoloAOP = angoloPOB perchè b è bisettrice, angoloPOB = angoloAO'O perché alterni interni).
Ricordando che nel rombo le diagonali sono perpendicolari otteniamo che OP è asse di AB.

Soluzione proposta da:
Classe 2a C LS "Giorgione" di Castelfranco V.to (TV)

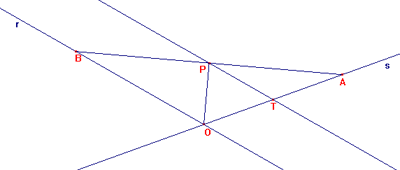
Parte 1^
Traccio la parallela ad una delle due rette (per es. alla retta “r”) passante per il punto P.
Segno il punto A simmetrico del punto O rispetto al punto T, intersezione della retta precedentemente tracciata con la retta “s”.
Traccio una retta passate per A e P e ottengo B sulla retta r. [[Ho ottenuto un fascio di rette parallele]] [Traccio per A la parallela alla retta "r"], applico il teorema di Talete: risulta che siccome AT è congruente a TO anche AP e' congruente a PB.

Parte 2^
Traccio la bisettrice di [uno degli] angoli formati dalle rette “s” e “r” e su di essa fisso il punto P. Traccio la perpendicolare alla bisettrice passante per P e ottengo i punti A, B sull’intersezione con le due rette iniziali.
Voglio dimostrare che AP è congruente a PB.
Considero i triangoli APO e BPO. Essi hanno: PO in comune, AOP[angolo] congruente a BOP[angolo] per ipotesi (bisettrice), APO[angolo] congruente a BPO[angolo] perché retti per costruzione. Pertanto APO congruente a BPO per il 2° criterio di congruenza dei triangoli.
Quindi AP è congruente a PB (lati [omologhi] di triangoli congruenti).

Soluzione proposta da:
Classe 2a E Liceo Scientifico “G. Galilei” Bitonto (BA)

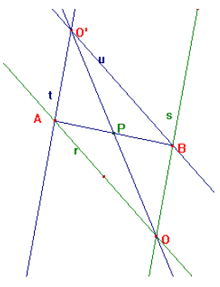
a) Disegnate le due rette incidenti r ed s e il punto P non appartenente ad esse, abbiamo individuato due modi per ottenere la costruzione dei punti A e B richiesti e soddisfacenti le condizioni imposte:
1) A appartenente ad r; 2) B appartenente ad s; 3) P punto medio di AB.

a) [...]

Secondo modo:

Costruita la retta u simmetrica di r rispetto a P e la retta t simmetrica di s rispetto a P, per la proprietà della simmetria assiale, le rette u ed r sono parallele, così pure t ed s. Detti A, B, O’ i punti di intersezione delle coppie di rette (r,t), (s,u) e (t,u), si ha che OBO’A è un parallelogrammo, avendo i lati opposti paralleli, e P ne risulta il centro di simmetria. Ne consegue che P è punto medio di AB.

b) [,,,]

Soluzione proposta da:
Valerio Borsò, classe 3D - LS "F. Buonarroti"

Ipotesi: proprietà delle simmetrie e delle rette parallele; P interno all'angolo.
Tesi: A appartiene ad s, B appartiene a r; AP=PB; A, B , P sono allineati

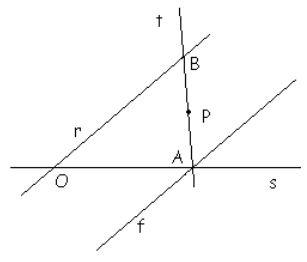
A) Per prima cosa utilizzo la simmetria centrale di centro P e costruisco f, simmetrica alla retta r.
Conoscendo le proprietà delle simmetrie (mantengono le distanze, gli angoli ecc..) posso dire che la retta f è parallela alla retta r e che se prendo un punto a caso D sulla retta r avrò il suo simmetrico D', [sulla retta f], tale che PD=PD'.
Nella mia libertà di scelta se prendo il punto A in modo che sia intersezione di s con f avrò il suo simmetrico B che appartiene alla retta r e tale che BP=PA allineati sulla retta t.

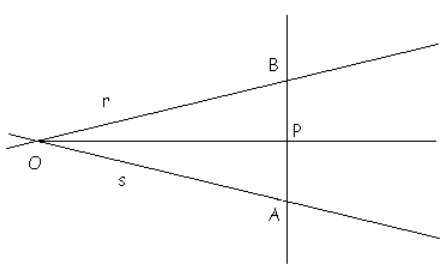
B) Prendo P sulla bisettrice dell'angolo; allora, sapendo che la bisettrice è anche l'asse di simmetria che scambia metà angolo con l'atra metà posso dire che (utilizzando la costruzione analoga a quella precedente): AP=PB e che OA=OB. Allora il triangolo OBA è isoscele e so che la mediana OP della base AB è anche asse della base. [[(e anche l'altezza), quindi gli angoli AP(^)O e BP(^)O sono retti.]]

Soluzione proposta da:
Alunni Paolo Agnes e Tania Amodeo
Classe 3^a P - S.M.S. di San Genesio (PV)

a) Abbiamo disegnato due rette incidenti; abbiamo preso un punto P sul piano non appartenente alle rette. Abbiamo disegnato la retta passante per O e P, e abbiamo preso il simmetrico di O rispetto a P.
Chiamiamo Q il punto trovato. Poiché P deve essere punto medio di AB, AB e OQ potrebbero essere le diagonali di un parallelogramma.
Per trovare A e B occorre disegnare il parallelogramma. Per trovare A abbiamo disegnato la parallela alla retta "s" passante per Q. Il punto A è l'intersezione delle due rette.
Per trovare il punto B abbiamo disegnato la parallela ad "r" passante per il punto Q.
Il punto B è l'intersezione delle due rette.

Soluzione proposta da:
Seconda classe A, turno mattina.
Scuola media Istituto "Dante Alighieri" di Rosario (Santa Fe, Argentina)
Nome degli alunni:
Armas, Alejandro. Baccino, M. Cecilia. Gorostiaga, Lucia. Lignos, Melina.
Martínez, Eugenia. Pérez, Luciana. Ronga, Joaquin. Sosa, Guadalupe.

a) [...]

b) [...]

Possibilità Nº 2
Il punto P deve essere costruito sulla bisettrice di [uno degli] angoli formati tra le rette r e s dato che: Se P è il punto medio del segmento AB, OP sarà asse del segmento AB se OP e AB saranno perpendicolari. [[Questo sarà vero, solo se]] [Allora] il triangolo OAB sarà isoscele, caso in cui OP è necessariamente la bisettrice dell’angolo AOB.

Soluzione proposta da:
Classe 3^a B Scuola Media L. da Vinci, Rufina (FI)

a) [...]

b) [...]

2) Ricordiamo che [[ogni punto sul]] la bisettrice [[è equidistante dai lati dell’angolo e che questa stessa]] è asse di simmetria dell’angolo. Immaginiamo quindi di prendere il punto P sulla bisettrice e di condurre per esso la perpendicolare alla bisettrice medesima: il segmento AB sarà diviso in due parti congruenti di [per] cui la bisettrice sarà anche asse. [[Inoltre avremo OA=OB, quindi il triangolo OAB sarà sempre isoscele.... ]]

Soluzione proposta da:
Classe 3a A - S.M.S. di Roveredo in Piano (PN)

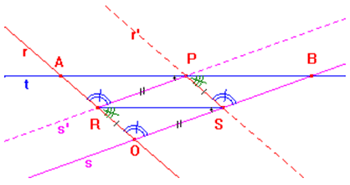
a) Date le rette r ed s incidenti in O ed il punto P non appartenente ad esse.

1. Retta s' parallela ad s, passante per P; sua intersezione R con r;
2. Retta r' parallela ad r, passante per P; sua intersezione S con s;
3. Segmento RS;
4. Parallela t al segmento RS, passante per P ;
5. Intersezioni di t: con r (A), con s (B).

• Il poligono OSPR è un parallelogramma per costruzione.
• I Triangoli PBS e RSO sono congruenti (gli angoli di vertice P ed R sono congruenti avendo i lati paralleli per costruzione, i segmenti PS ed RO sono lati opposti del parallelogramma e quindi congruenti, gli angoli di vertice S ed O sono congruenti perché i lati risultano paralleli per costruzione); anche il triangolo APR risulta congruente con RSO (il ragionamento è analogo a quello sopra).
• Consegue che i segmenti AP e PB sono congruenti (essendo congruenti ad RS), quindi P è il punto medio del segmento AB (della retta t).

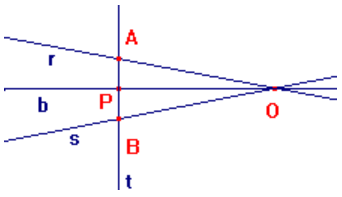
b) La bisettrice (b) è asse di simmetria dell'angolo; posto P sulla bisettrice si traccia la perpendicolare ad essa passante per P e si determina il segmento AB intersecandola con i lati dell'angolo; A e B risultano simmetrici rispetto b e P è il punto medio del segmento AB.

| Home Page Cabri | Torna a FLATlandia | Archivi |