 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Novembre 2001
Il testo del problema:
Sia ABC un triangolo qualunque.
Da un punto S sul lato AB condurre la retta parallela al lato CB fino ad
incontrare in P il lato AC.
Siano R e Q le proiezioni ortogonali di S e P sulla retta CB.
a) Di quale tipo è il quadrilatero SPQR?
b) Determinare una possibile posizione per il punto S affinché l'area di SPQR sia la metà dell'area di ABC. Tale posizione è unica?
(Facoltativo)
c) Qualora sia verificata la condizione (b), a quale ipotesi deve soddisfare il
triangolo ABC affinché SPQR sia un quadrato?
Motivare le risposte.
Commento
Care ragazze, cari ragazzi,
abbiamo ricevuto quattordici risposte: sei provengono dalle scuole medie
inferiori, sette dalle dalle scuole superiori e una di provenienza sconosciuta.
Le scuole che hanno partecipato sono:
Il problema proponeva di inscrivere un rettangolo in un triangolo e di individuare due situazioni particolari: quando la superficie del rettangolo è metà di quella del triangolo e, in tal caso, quando il quadrilatero diventa quadrato. Era richiesta come facoltativa la dimostrazione della unicità del caso particolare.
Il problema è stato affrontato in vari modi. Chi ha
utilizzato i teoremi della geometria euclidea (proprietà dei punti medi,
similitudine), chi ha fatto ricorso alle proprietà della simmetria (centrale o
assiale).
L'uso delle simmetrie ha ingenerato però qualche confusione; qualcuno ha
iniziato introducendo la simmetria e concluso con la congruenza dei triangoli,
producendo un eccesso di giustificazioni; qualcuno invece si è basato sulla
evidenza della simmetria tralasciando alcune necessarie giustificazioni.
Pochi hanno tentato la dimostrazione della unicità, senza riuscirvi. Un modo per verificare la unicità del rettangolo la cui area sia metà di quella del triangolo, è di cercare la soluzione per via algebrica. Ricorrendo alla similitudine si giunge ad una semplice equazione di primo grado, la cui soluzione, se esiste, è unica.
Poche sono le risposte completamente corrette. Molti hanno
considerato nell'ultima parte del problema solo casi particolari. Ben cinque
risoluzioni sono inaccettabili per incompletezza o mancanza delle
giustificazioni.
Inoltre, anche nelle risposte accolte, abbiamo riscontrato varie imprecisioni
nella esposizione.
Una di queste è la confusione fra proiezione ortogonale e distanza.
Abbiamo scelto di riportare le seguenti soluzioni:
Per le scuole medie inferiori
Per le scuole superiori
NOTA: Le correzioni al testo o i commenti sono scritti in parentesi quadra. Sono racchiuse in doppia parentesi quadra le parti ritenute superflue.
Soluzione proposta da:
Alunni: Feroldi F. 3C, Rovesti P. 3C, Masella M. 3A, Fanetti G. 3A
Istituto Comprensivo 2 - S. M. Suzzara (MN)
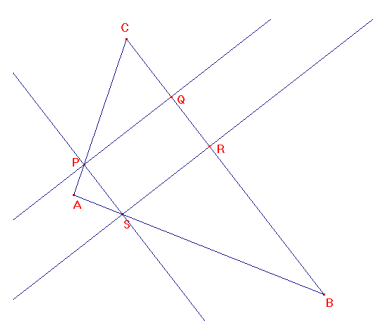
A) il quadrilatero SPQR è un rettangolo infatti, SP è parallelo a QR per costruzione, SR parallelo a PQ perché perpendicolari allo stesso lato CB; inoltre gli angoli in Q ed R sono entrambi retti (perché Q ed R sono le proiezioni di P ed S su BC) di conseguenza sono retti anche gli angoli P ed S.
B) Il punto S deve essere posizionato nel punto medio del lato AB. In questo caso tracciando la parallela al lato BC che passa per A otteniamo un fascio di rette parallele tagliate da alcune trasversali. Poiché S è il punto medio di AB, P è punto medio di HQ. PS, unendo i punti medi di due lati di un triangolo, è metà del terzo lato.
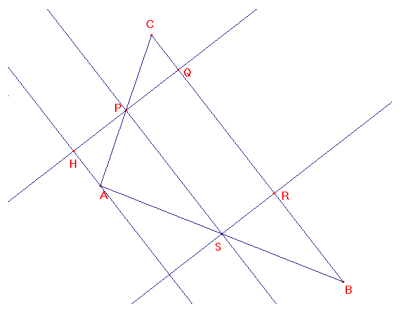
L'area del rettangolo SPQR è PS x PQ; l'area del triangolo ABC è (BC x QH) / 2; poiché BC = 2PS e QH = 2PQ, l'area del triangolo ABC è (2PSx 2PQ)/ 2 = 2(PS x PQ), cioè l'area del triangolo è doppia dell'area del rettangolo.
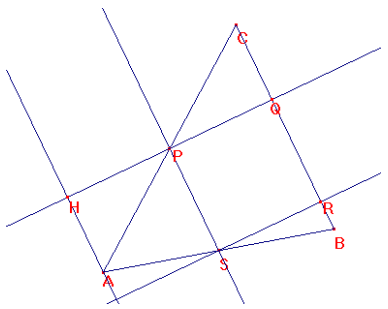
C) La base BC del triangolo ABC deve essere uguale all'altezza HQ ad essa relativa; in questo caso, infatti, i due lati consecutivi (PS e PQ) del rettangolo risultano uguali perché metà di segmenti uguali.
Soluzione proposta da:
Classe 3 B - SM "L. da Vinci"
- Rufina (FI)
A) Di che natura sarà il poligono SRPQ?
Il poligono SPQR è un rettangolo perché costruito tracciando le parallele
SP a CB e le perpendicolari passanti a S e P al lato CB medesimo [risultando
cosi' perpendicolari anche a CB].
B) Quale posizione dovrà assumere il punto S affinché l'area del
poligono SPQR sia equivalente alla metà dell'area del triangolo ABC?
Perché si verifichi la condizione richiesta il punto S dove essere preso
sul punto medio del lato AB.
Considero infatti il triangolo ABC costituito dal poligono SPQR e dai triangoli SRB,PCQ,PAS. Con simmetria centrale costruisco il simmetrico dei due triangoli SRB e PCQ (centro in S, punto medio di AB e centro in P punto medio di AC); si forma così un rettangolo SPQ'R' [occorre prima dimostrare l'allineamento dei punti R', A, Q', come evidenziato nella figura] equivalente al rettangolo SPQR perché hanno stessa [uguale o congruente] altezza e stessa base.
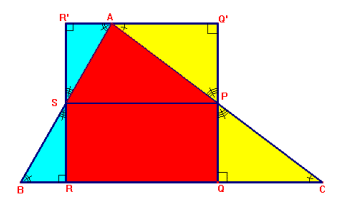
Inoltre il rettangolo QRR'Q' è equivalente al triangolo ABC perché composto dalle stesse figure del triangolo.
C) Quale ipotesi deve soddisfare il triangolo ABC affinchè SPQR
sia un quadrato?
Per quanto già detto la condizione richiesta si verifica nel caso in cui il
poligono QRR'Q' sia un rettangolo con le dimensioni una doppia dell'altra.
Quindi il triangolo ABC di partenza dovrà avere altezza e base uguali.
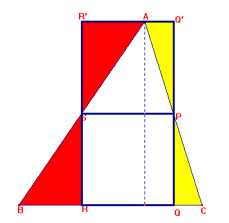
Soluzione proposta da:
Gruppo: De Bernardi - Ferrario - Gallazzi - Mecchina - Santoro - Vargiu
S.M.S. "E. De Amicis" - Busto Arsizio (VA) Classe 3°D
B) [Sia S punto medio di AB]
Ribaltando (simmetria assiale con asse SP) il quadrilatero SPQR attorno al lato SP ottengo il rettangolo SPXZ che è uguale a SPQR perchè il movimento è una isometria. Allora il quadrilatero QRZX è equivalente al triangolo ABC in quanto i triangoli SAZ e SBQ come AXP e PRC sono uguali secondo il 1° criterio di uguaglianza [Occorre prima dimostrare che il punto A appartiene al lato SZ].
Per i triangoli SAZ e SBQ :
- Gli angoli: BSQ = ZSA perchè opposti al vertice
- SB = SA e SQ = SZ per costruzione.
Per i triangoli PRC e PAX:
- Gli angoli: SPC = APX perché opposti al vertice
- AP = PC per il teorema di Talete.
Pertando QRXZ è equivalente a ABC ed è il doppio di SPQR.
SPQR è metà di ABC.
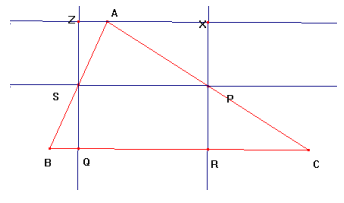
C) La dimostrazione è ovvia! Qualora sia verificata la
condizione (B), il triangolo ABC deve soddisfare alla condizione che la base CB
e la relativa altezza AK devono essere congruenti!
Infatti [supposto che SPQR sia un quadrato] AK è il doppio del lato del
quadrato, la lunghezza di CQ più quella di RB equivale alla lunghezza del lato
SP, ma la base [CB] è composta da: CQ, RB e il lato del quadrato; quindi
l'altezza AK é uguale alla base CB.
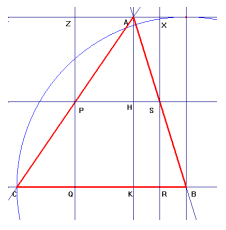
Soluzione proposta da:
Classe 3^ A - S. M. di Roveredo in Piano
(PN)
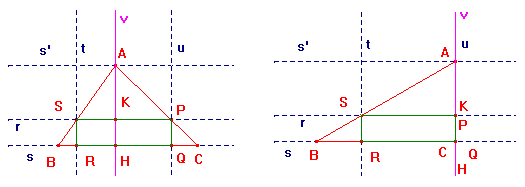
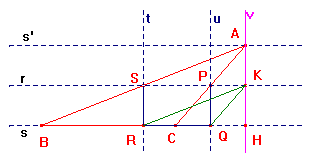
COSTRUZIONE.
1. Due rette parallele (s, s');
2.Triangolo ABC: A su s', B C su s;
3. Costruzione come indica il testo del problema (... retta r parallela a s per
S; retta t perpendicolare a s, per S; retta u perpendicolare a s per P; .....);
4. Retta v, perpendicolare a s e passante per A;
5. Intersezione H di v con s; intersezione K di v con r.
Consideriamo A punto di animazione: * H ( piede dell'altezza relativa al lato BC dal vertice A) coincide con A o con B (triangolo rettangolo); * è esterno al segmento AB (triangolo ottusangolo); * sta tra A e B (il triangolo può essere rettangolo, acutangolo, ottusangolo, l'angolo di vertice A dipende dalla distanza delle rette s, s' e dal segmento BC).
a)
Il quadrilatero SPQR è rettangolo per costruzione (lati opposti su rette
parallele e gli angoli risultano retti perché ottenuti disegnando le rette t ed
u perpendicolari ad s ed r).
b)
COSTRUZIONE
6. Segmenti RK, KQ.
Il punto S coincide con il punto medio del lato AB.
Soluzione proposta da:
Alunni: Agnes, Amodeo, Braschi, Civardi, Izzo, Loffredo, Pozzato, Tasti
Classe III P - S.M. "Dalla
Chiesa" - S. Genesio (PV)
a) La figura SPQR ha due coppie di
lati opposti paralleli ( BC//SP per costruzione e SR//PQ perché rette
perpendicolari ad una stessa retta). E’ quindi un parallelogramma. Dal momento
che possiede anche 2 angoli retti per costruzione, è un rettangolo.
Ci accorgiamo che il triangolo ABC e il triangolo ASP sono simili: questo
perché SP//BC e quindi gli angoli PCB=APS e CBS=PSA perché sono angoli
corrispondenti; l’angolo BAC è in comune.
b) Per fare in modo che l’area di SPQR sia la metà dell’area di ABC, il punto S deve coincidere con il punto medio del lato AB.
- B è il simmetrico di A in una simmetria centrale di
centro S.
Il punto P è punto medio di AC, dato che i triangoli ABC e ASP sono simili, di
conseguenza anche il punto C è simmetrico di A in una simmetria centrale di
centro P.
- Tracciamo una retta parallela ai segmenti SP e BC
passante per il punto A e la chiamiamo “s”.
Prolungo PQ e chiamiamo M il punto d’intersezione con la retta “s”.
Prolungo RS e chiamiamo N il punto d’intersezione con la retta “s”.
I due triangoli PCQ e AMP sono congruenti. Lo deduciamo dal fatto che si
corrispondono in una simmetria centrale di centro P perché: [la dimostrazione
che segue e' superflua se si fa notare che M e' il simmetrico di Q]
- PA=PC
- (gli angoli) CQP=PMA perché angoli retti
- (gli angoli) QPC=MPA perché angoli opposti al vertice
Per gli stessi motivi anche i triangoli SNA e SRB sono
congruenti perché si corrispondono in una simmetria centrale di centro.
Il rettangolo MNRQ è equiesteso al triangolo ABC per somma di figure
congruenti. Poiché NS=RS, il rettangolo SPQR ha area uguale 1/2 dell’area
MNRQ, quindi l’area di SPQR è uguale a ½ dell’area di ABC.
[...]
Soluzione proposta da:
Monica Landoni
Classe 2LT - Liceo scientifico tecnologico
Istituti Istruzione Superiore "Cesaris" - Casalpusterlengo (Lodi)
a)
Il quadrilatero ottenuto è un rettangolo. E’ un parallelogramma perché ha PS
// CB per costruzione,
PQ ed RS sono le [[...]] distanze di due rette parallele, quindi sono
isometriche e parallele.
E’ un rettangolo perché PQ ed RS ( distanze) formano angoli retti .
b)
L’unica [Una] posizione per cui è possibile il verificarsi del rapporto tra
le due aree è quando il punto S è il punto medio di AB. Infatti, in tal caso,
[per la proprietà dei punti medi ...] abbiamo che PS è [[pari al]] la metà di
BC; per questo anche SR è metà dell’altezza AH.
L’area del triangolo si trova facendo il semiprodotto tra l’altezza e la
base del triangolo; allora l’area del triangolo è uguale al prodotto tra BC e
AH diviso 2.
L’area del rettangolo è data da RQ * SR =1/2BC * 1/2AH =1/4(BC *AH) = 1/2
area (ABC).
c)
Il triangolo ABC, di base AB, dovrebbe avere l’altezza AH isometrica alla
base, in tal caso i lati del rettangolo, isometrici rispettivamente a metà base
e a metà altezza risultano uguali.
Soluzione proposta da:
Marco Guernieri e Riccardo Zambarbieri
Classe 2^A s t - Istituto "E. Ferrari" (TO)
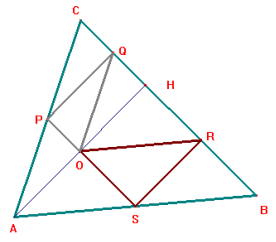
B)
S deve coincidere con il punto medio di AB.
Infatti, per il teorema di Talete P coinciderà con il punto medio di AC.
Conducendo il segmento AH perpendicolare a CB, che
incontra PS in O, il triangolo ABC viene suddiviso in due triangoli rettangoli,
composti a loro volta da quattro triangoli congruenti.
AHC=AOP+OPQ+PQC+OHQ=4*OPQ
ABH=ASO+SBR+ORH+SRO=4*SRO
Il rettangolo SPQR è composto da quattro triangoli uguali
a due a due:
SPQR=2*OPQ+2*SRO
ABC=2*SPQR
Dimostro che i triangoli OHQ e OPQ sono congruenti:
-OQ in comune
-gli angoli OHQ e OPQ sono congruenti perché retti
-gli angoli POQ e OQH sono congruenti perché alterni interni (parallele PS e
CB, trasversale OQ)
Analogamente si dimostra che AOP è congruente a PQC ed a OPQ.
Dimostro che ASO e SBR sono congruenti:
-AS=SB perché S è il punto medio di AB
-gli angoli OSA e RBS sono congruenti perché corrispondenti (parallele OS e RB,
trasversale AB)
-gli angoli OAS e RSB sono congruenti perché corrispondenti (parallele OA e RS,
trasversale AB)
Analogamente si dimostra che anche i triangoli ORH e SRO sono congruenti ad ASO e SBR.
| Home Page Cabri | Torna a FLATlandia | Archivi |