 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Marzo 2002
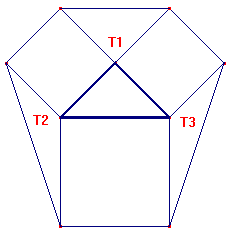
a) Disegnare un quadrato su ciascun lato di
un triangolo rettangolo isoscele. Congiungendo i vertici dei quadrati,
come nella figura allegata, si ottengono tre triangoli T1, T2, T3 fra loro
equivalenti.
Dimostrare tale affermazione.
b) La proprietà precedente vale anche nel caso
di un qualsiasi triangolo?
Giustificare la risposta.
Commento
Abbiamo ricevuto quindici risposte: dieci dalle scuole medie inferiori e cinque
dalle scuole superiori.
Le scuole che hanno partecipato sono:
Nel problema di Marzo si chiedeva di dimostrare
l'equivalenza di tre triangoli che si formano costruendo un quadrato su ciascun
lato di un triangolo assegnato. In questo mese è stata introdotta una novità
rispetto al metodo finora seguito: onde evitare noiose descrizioni, è stata
allegata al testo la figura relativa al caso particolare proposto nella prima
parte del problema. Non era richiesta giustificazione della sua costruzione.
La particolare situazione raffigurata, in cui era evidente la congruenza di uno
dei tre triangoli da esaminare con quello assegnato, aveva lo scopo di suggerire
il percorso più immediato per risolvere poi il problema nel caso generale
richiesto nella seconda parte: bastava infatti dimostrare l'equivalenza con il
triangolo dato di uno solo dei tre triangoli ottenuti dalla costruzione.
I ragazzi della scuola media hanno dimostrato di aver gradito questo tipo di
problema e hanno risposto in numero superiore al solito. Purtroppo molti hanno
considerato, anche nella seconda parte, solo situazioni particolari: triangolo
rettangolo scaleno o triangolo non rettangolo, ma isoscele.
Qualcuno ha dichiarato di non saper risolvere il caso generale, qualcuno ha
affermato che questo non vale (per chi usa software geometrici basta una
verifica numerica, calcolando l'area, per accorgersi del contrario).
Anche fra i ragazzi delle scuole superiori c'è chi non ha interpretato
correttamente il testo del problema nella seconda parte.
In generale si sono delineati due percorsi di risoluzione: c'è chi ha fatto
ricorso al calcolo delle aree, chi ha indagato sulle proprietà geometriche della
figura, utilizzando le proprietà del quadrato, la congruenza di opportuni
triangoli rettangoli o le trasformazioni geometriche.
Nessuna delle soluzioni proposte è completamente valida in quanto chi ha
individuato il percorso più immediato ha poi commesso imprecisioni e/o errori
nelle giustificazioni; chi ha presentato una soluzione corretta nella
esposizione non ha però individuato il modo più breve per la dimostrazione.
Prima di presentare le soluzioni scelte è opportuno fare ancora una
osservazione. Non è corretto affermare la congruenza degli angoli di due
triangoli rettangoli dicendo che sono complementari o la congruenza di due
angoli dicendo che sono differenza di angoli supplementari: due angoli sono
congruenti fra loro se sono complementari (o supplementari) di uno stesso angolo
(o di angoli congruenti) e, ancora, due angoli sono congruenti se sono somma o
differenza di angoli congruenti (non complementari o supplementari).
Sono state scelte le soluzioni inviate da:
NOTA: come al solito, le correzioni e i commenti sono inseriti in parentesi quadra.
Soluzione Proposta da:
Classe 2A (prima parte) e Classe 3A (seconda parte)
S.M. "Zanella", Roveredo in Piano (PN)
a) (classe 2A)
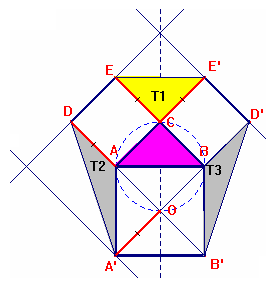
Il triangolo ABC (rettangolo isoscele, rettangolo in C) ha i cateti congruenti con metà diagonale del quadrato ABB'A' (quadrato costruito sull'ipotenusa AB) ed è congruente col triangolo T1;
Del triangolo T2 consideriamo il lato AD e la sua altezza A'O, congruenti ai cateti del triangolo T1. I Triangoli T1 e T2 sono equivalenti.
Analogo ragionamento vale per T1 e T3.
b) (classe 3A)
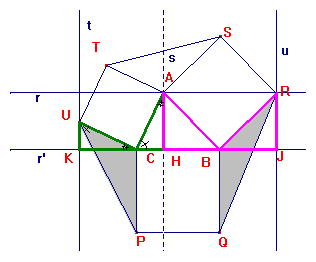
Costruiamo il triangolo ABC con A sulla retta
r parallela al lato CB (retta r’). Triangolo T1, di vertici AST; triangolo T2,
di vertici PCU, triangolo T3, di vertici QRB.
Questa costruzione ci permette di studiare il movimento della figura
all’animarsi di A sulla retta sui cui è posto, in particolare otteniamo i luoghi
di U e di R, luoghi che ci hanno suggerito come procedere nel ragionamento [i
luoghi, qui "osservati" ma non giustificati, si formano solo in questa
particolare costruzione in cui il punto A si muove su una retta parallela a CB e
il segmento CB resta fisso].
Retta s, perpendicolare ad r’per A e loro intersezione H;
Retta t perpendicolare ad r’(o parallela ad s) per U e loro intersezione K (è luogo di U all'animarsi di A su r); retta u perpendicolare ad r’(o parallela ad s) per R e loro intersezione J (è luogo di R all'animarsi di r);
I triangoli UKC e AHC sono congruenti (sono
rettangoli, rispettivamente, in K ed in H e le ipotenuse sono lati consecutivi
del quadrato CATU, gli angoli in C [KCU e HCA]sono complementari e lo sono
anche rispettivamente degli angoli di vertice U [KUC] e di vertice A [HAC]
[quindi HCA=KUC perché complementari dello stesso angolo); sono congruenti
anche i triangoli AHB e BJR (ragionamento analogo a quello sopra).
Segue che i segmenti KC, AH, BJ risultano congruenti.
I triangoli UCP (T2) e QBR (T3) (anche il triangolo ABC) sono equivalenti avendo un lato ( è lato del quadrato CBQP) e la rispettiva altezza congruenti (lato CP e altezza CK, lato BQ e altezza BJ).
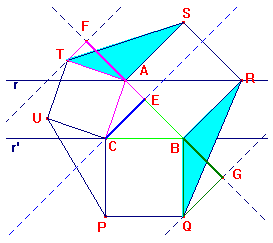
Facciamo un’analoga costruzione per i triangoli TAS (T1) e BQR (T3) in cui i segmenti AF, CE, BG sono congruenti; i triangoli T1, T2, T3, quindi, sono equivalenti.
Il caso a) (triangolo rettangolo isoscele) è un caso particolare per il quale valgono le stesse conclusioni.
Soluzione Proposta da:
Classe 3A - Scuola Media di Venasca (CN)
a)
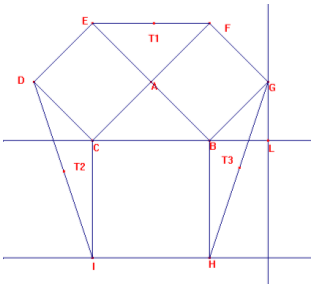
Indicata con l la misura dei cateti del triangolo
rettangolo isoscele ABC assegnato (vedi figura), T1 è anch’esso, per
costruzione, un triangolo rettangolo isoscele e congruente ad ABC, per cui la
sua area è uguale a 1/2 l^2.
T3 è equivalente a T1 perché la sua area si ottiene moltiplicando l’altezza BL
per la base BH, fratto 2.
Ma BH=BC=l*sqr(2) e BL = l/sqr(2) perché è il lato del triangolo rettangolo
isoscele avente BG come ipotenusa.
Quindi l’area di T3=1/2 BH*BL = 1/2 di l*sqr(2)*(l/sqr(2)) = 1/2 l^2.
T3 e T2 sono triangoli congruenti per il primo criterio di congruenza dei
triangoli in quanto hanno congruenti due lati (DC= BG e CI= BH) e l’angolo fra
essi compreso (rispettivamente DCI e GBH = 135°)
Pertanto i tre triangoli T1, T2 e T3 sono equivalenti c.v.d
Soluzione Proposta da:
Davide Montalbano, Ilaria Andena, Sarah Taha, Silvia Gasti
Classe IIIM - S.M. "Bergamaschi", Torrevecchia Pia (PV)
La manipolazione della figura mediante gli strumenti di Cabri II ci ha suggerito di partire con la dimostrazione richiesta al punto b)
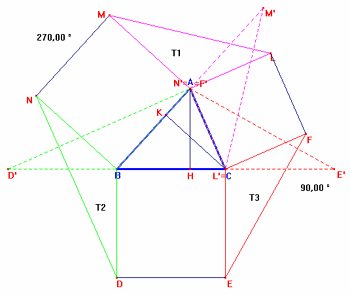
Considerato che:
la rotazione di 270° in senso antiorario di centro B, trasforma il triangolo
T2 nel triangolo D’N’B con N’![]() A
[essendo NB=BA perché lati dello stesso quadrato] e D’ allineato con B e C
(infatti l’angolo D’BA è congruente all’angolo DBN, essendo il suo
corrispondente in una rotazione, e perciò è anch’esso supplementare di ABC, per
cui BD’ e BC sono semirette opposte). Quindi AH, altezza del triangolo ABC
relativa alla base BC, è altezza anche del triangolo D’N’B relativa alla base
D’B. I due triangoli ABC e D’N’B, avendo basi congruenti (D’B = BD perché
corrispondenti in una rotazione e BD = BC perché lati di un quadrato e quindi,
per la proprietà transitiva della congruenza, BC = D’B) e altezza ad esse
relative in comune, hanno la stessa area. Per la proprietà transitiva, essendo T2
congruente e quindi equivalente a D’N’B, è
A
[essendo NB=BA perché lati dello stesso quadrato] e D’ allineato con B e C
(infatti l’angolo D’BA è congruente all’angolo DBN, essendo il suo
corrispondente in una rotazione, e perciò è anch’esso supplementare di ABC, per
cui BD’ e BC sono semirette opposte). Quindi AH, altezza del triangolo ABC
relativa alla base BC, è altezza anche del triangolo D’N’B relativa alla base
D’B. I due triangoli ABC e D’N’B, avendo basi congruenti (D’B = BD perché
corrispondenti in una rotazione e BD = BC perché lati di un quadrato e quindi,
per la proprietà transitiva della congruenza, BC = D’B) e altezza ad esse
relative in comune, hanno la stessa area. Per la proprietà transitiva, essendo T2
congruente e quindi equivalente a D’N’B, è
T2 equivalente al triangolo ABC.
Analogamente dimostriamo che gli angoli ACB e FCE sono supplementari e che la rotazione di 90° in senso antiorario di centro C porta F in A e E in E’ allineato con B e C. Quindi AH è altezza anche del triangolo ACE’ relativa al lato CE’ per cui i triangoli ABC e ACE’ sono equivalenti e di conseguenza
T3 è equivalente al triangolo ABC
Ripetiamo un procedimento analogo sul triangolo T1. Poiché gli angoli MAL e CAB sono supplementari e AL = AC perché lati di un quadrato, la rotazione di 270° in senso antiorario di centro A, porta L in C e M in M’ allineato con A e B. Il segmento CK è perciò altezza relativa al lato AB nel triangolo ABC e altezza relativa al lato AM’ nel triangolo ACM’ e poiché è anche M’A = AB (perché entrambi uguali ad MA), i triangoli ABC e ACM’ sono equivalenti. Di conseguenza
T1 è equivalente al triangolo ABC
Per la proprietà transitiva della relazione di equivalenza, essendo T1, T2, T3 equivalenti al triangolo ABC, sono tra di loro equivalenti.
Il caso del triangolo rettangolo isoscele considerato al punto a) è solo un caso particolare, che risulta così dimostrato.
Soluzione Proposta da:
Classe II E - L.S. “G. Galilei” Bitonto (BA)
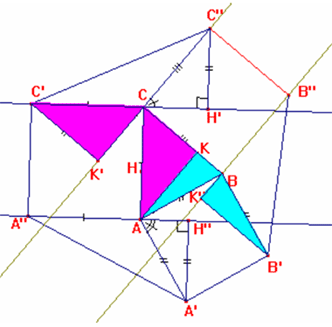
a) I triangoli AA’A” e BB’B” sono
congruenti e quindi equivalenti per il primo criterio di congruenza (AA”=BB”,
AA’=BB’, gli angoli A”AA’=B”BB’ =135°). CC’C” è equivalente ai primi due per
avere base e altezze congruenti (CC’=AA”=BB”, CC”=A’H=B’H).
Quest’ultima relazione discende dal fatto che le rette AA” e BB” essendo
inclinate [formando un angolo] di 45° su AA’ e BB’ contengono le diagonali del
quadrato costruito su AB, che sono tra loro perpendicolari e tali che A’H=B’H=AC.
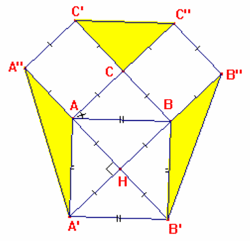
b) Anche se il triangolo ABC è
qualsiasi, continua a sussistere la proprietà, cioè i triangoli AA’A”, BB’B” e
CC’C” sono equivalenti.
Infatti si riconosce (fig. 1) che AA’A” e CC’C” hanno le basi congruenti (AA”=CC’
lati opposti dello stesso quadrato) e le altezze congruenti (C”H’=A’H” perché
entrambi congruenti a BH, altezza relativa al lato AC in ABC, come si deduce
dalla congruenza delle coppie di triangoli rettangoli CH’C” e CHB ed ancora BHA
e AA’H”. Infatti questi hanno le ipotenuse congruenti in quanto lati dello
stesso quadrato e angoli acuti congruenti perché complementari dello stesso
angolo: C”CH’=HCB e HAB=H”AA’).
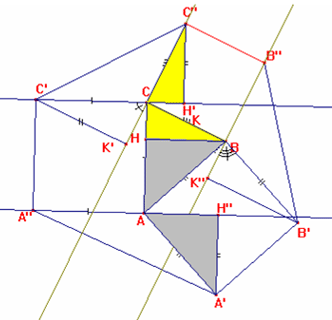
In maniera analoga (fig. 2), CC’C” e BB’B”
sono equivalenti per avere le basi congruenti (CC”=BB”) e le altezze (C’K’=B’K”)
congruenti, in quanto congruenti entrambi a AK, altezza relativa al lato CB in
ABC, cosi come si deduce dalla congruenza dei triangoli rettangoli CC’K’=CAK e
B’BK”=ABK.
Da quanto dimostrato per transitività si deduce la tesi.
Soluzione Proposta da:
Cristina
Bernacchia
Classe II C LS "Michelangelo" - Forte dei Marmi (LU)
Risposta domanda a)
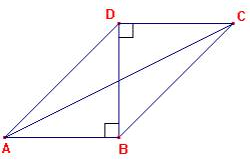
Costruisco il triangolo ABD uguale per
costruzione al triangolo T1 avente l'angolo retto in B.
Costruisco poi BCD uguale al triangolo T1, esso ha BD in comune con il triangolo
ABD e l'angolo retto in D. Prendendo in considerazione il quadrilatero ABCD
unisco poi A con C. Si formano così due triangoli, ACD e ACB, essi hanno un lato
che coincide con il cateto AB e [o] DC, un secondo lato che coincide con
l'ipotenusa AD e [o] BC, l'angolo ADC = ABC dato che essi sono formati da
90°+45° = 135° e che somma di angoli
uguali sono uguali.
Allora per il primo criterio di uguaglianza i due triangoli ACD e ACB sono
uguali. Inoltre i due sono uguali a T2 e T3 poiché un lato è un cateto del
triangolo iniziale T, l' [un] altro uguale all'ipotenusa e l'angolo compreso tra
essi è 360°-90°-90°-45°=135° allora per il primo criterio di uguaglianza
T[2]=T[3]=ADC=ABC.
Sapendo che ABCD può essere formato da due triangoli uguali a T1, o dai due
triangoli T2 e T3, [[...]] T1, T2, T3 sono equivalenti [perché ciascuno è metà
della stessa superficie].
| Home Page Cabri | Torna a FLATlandia | Archivi |