 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Maggio 2002
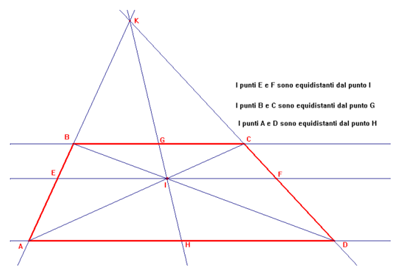
In un qualunque trapezio ABCD sia I il punto in cui si intersecano le diagonali AC e BD.
a) Condurre per I la retta parallela alle basi del
trapezio. Essa incontra i lati obliqui AD e BC rispettivamente in E e F. Che
cosa rappresenta il punto I per il segmento EF?
b) Prolungare i lati obliqui, sia K il loro punto di incontro. In quali punti la
retta IK taglia le basi del trapezio?
Motivare le risposte.
Figura inviata dagli alunni delle
classi quinte
Scuola Elementare “Galileo Galilei” - Alessandria
COMMENTO
Nel mese di Maggio abbiamo ricevuto undici risposte una delle quali da una scuola elementare. Le restanti dieci risposte si sono distribuite in modo uguale fra scuole medie inferiori e superiori, alcune scuole hanno inviato più di una soluzione.
Le scuole che hanno partecipato sono:
Consapevoli del gravoso lavoro di chiusura dell'anno
scolastico, abbiamo proposto per il mese di Maggio un problema abbastanza
semplice che, articolato in due parti, conduce a scoprire una proprietà presente
in tutti i trapezi: la retta che congiunge il punto comune alle diagonali con il
punto comune ai prolungamenti dei lati obliqui, divide a metà le due basi.
C'è chi, approfondendo l'indagine sulla figura, ha scoperto una caratteristica
ancor più generale che riporteremo nelle soluzioni da proporre all'attenzione
dei partecipanti sul sito web di FLATlandia.
Le soluzioni pervenute non presentano in sostanza errori di rilievo. Tuttavia,
come spesso succede quando le proprietà della figura sono immediate, si
riscontrano in alcune di esse considerazioni non opportunamente introdotte o
conclusioni affrettate. Come di consueto saremo più severi con i ragazzi della
scuola superiore che dovrebbero, a questo
punto dell'anno scolastico, saper gestire in modo esauriente una dimostrazione,
una volta individuato il ragionamento che porta alla soluzione del quesito
proposto.
Riteniamo, in proposito, di dover esprimere alcune osservazioni:
Abbiamo apprezzato il lavoro della quinta classe di scuola
elementare.
Utilizzeremo la loro figura per presentare il problema sul sito web. Abbiamo
scelto inoltre di presentare le seguenti soluzioni:
NOTA: come al solito, le correzioni e i commenti sono inseriti in parentesi quadra. Le parti superflue o quelle mancanti in doppia parentesi quadra.
Soluzione proposta da
Taha Sarah, Andena Ilaria, Montalbano Davide, Di Miceli Rosalinda, Secchi
Federica, Baietta Fabiola
classe 3M Scuola media “Bergamaschi” di Torrevecchia Pia (PV)
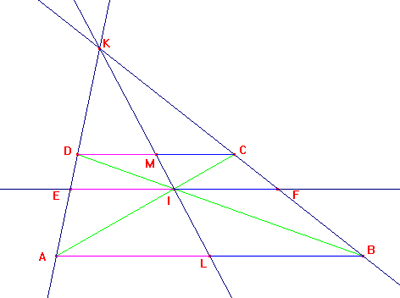
a) Considero i triangoli ADB e EDI; hanno
I due triangoli, per il primo criterio di similitudine,
sono simili; quindi
AB : EI = AD : DE (*)
Analogamente dimostro che sono simili i triangoli ABC e CFI; quindi
AB : IF = CB : CF (*)
Considero le parallele AB, EF, DC tagliate dalle trasversali DA e CB; per il
teorema di Talete
DA : ED = CB : CF
perciò i rapporti al secondo membro delle proporzioni (*) sono uguali, quindi
risulta
AB : EI = AB : IF dalla quale, applicando la proprietà del permutare delle
proporzioni, ottengo
AB : AB = EI : IF e perciò
EI = IF, ossia I è il punto medio di EF
b) In modo analogo dimostro che M, punto di
intersezione di DC con la retta KI, è punto medio di DC.
Considero i triangoli KDM e KEI. Essendo DM e EI parallele, i triangoli sono
simili, per il primo criterio di similitudine e quindi
DM : EI = KD : KE
Analogamente dimostro che sono simili i triangoli KMC e KIF, per cui
MC : IF = KC : KF
per il teorema di Talete è
KD : KE = KC : KF e quindi dalle proporzioni precedenti si ricava che
DM : EI = MC : IF --> DM : MC = EI : IF ma essendo EI = IF, per la
dimostrazione a) ricavo
DM = MC, ossia M è il punto medio di DC
In modo analogo, per la similitudine dei triangoli KEI e
KAL [dove L è il punto di intersezione della retta IK con la base AB], scrivo
EI : AL = KE : KA
e per la similitudine dei triangoli KIF e KLB
IF : LB = KF : KB
inoltre per il teorema di Talete è
KE : KA = KF : KB e quindi
EI : AL = IF : LB --> EI : IF = AL : LB per cui
AL = LB, ossia L è punto medio di AB
Soluzione proposta da
Classe 2 A: Prima parte (a). Redivo
Nicolò (3 A): Seconda parte (b).
Scuola Media di Roveredo in Piano (PN)
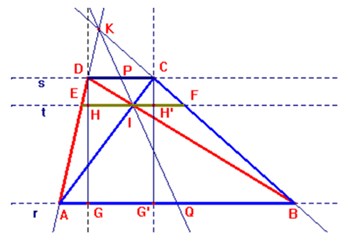
a) (Classe 2 A.)
Il trapezio è stato costruito su due rette (r, s) parallele (A,B su r; DC su s).
La retta t è parallela a r per I. Retta perpendicolare ad r per D, sue
intersezioni con r (G) e con t (H); retta perpendicolare a r per C e sue
intersezioni con r (G’) e con t (H’).
1. I triangoli ABD, ABC: - sono equivalenti (stesso lato [base] AB e stessa altezza del trapezio); - hanno in comune il triangolo ABI che viene sottratto da entrambi: dal triangolo ABD si ottiene il triangolo AID e da ABC otteniamo il triangolo BCI. Quindi i triangoli ADI e BCI sono equivalenti.
2. Triangolo ADI è la somma dei triangoli EID e AIE che hanno in comune il lato EI e le cui altezze DH e HG (rispetto al lato [base] EI) danno per somma l’altezza del trapezio DG. Anche la somma dei segmenti CH’ (altezza del triangolo IFC rispetto al lato [base] IF) e H’G’ (altezza del triangolo BFI rispetto al lato [base] IF) è altezza del trapezio (i triangoli IFC e IBF hanno il lato IF in comune e danno per somma il triangolo BCI).
3. I segmenti DH e CH’ sono congruenti (distanza di due rette parallele) e li indichiamo con “h”; i segmenti HG e H’G’ sono congruenti (distanze tra le rette r e t) e li indichiamo con “k”. Calcoliamo le doppie aree dei triangoli equivalenti AID e BCI che indichiamo con 2A: EI * h + EI * k = 2A; IF * h + IF * k = 2A. Consegue che le misure di IE e IF sono uguali, quindi il punto I è il punto medio del segmento EF.
b) (Nicolò Redivo, Classe 3 A)
(La classe 2^ non ha ancora consolidato le conoscenze sulla similitudine).
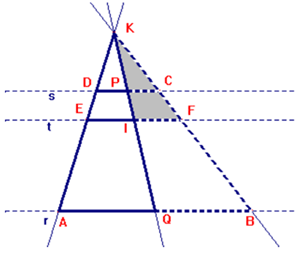
I triangoli KPC e KIF risultano simili (angoli corrispondenti congruenti essendo i lati [DC ed EF] paralleli per costruzione); vale la proporzione tra le misure dei lati: KP : KI = PC : IF; anche i triangoli KDP e KEI sono simili per la congruenza degli angoli [corrispondenti], per cui vale: KP : KI = DP : IE. Dalle due proporzioni possiamo scrivere: PC : IF = DP : IE (permutando i medi, PC : DP = IF : IE), da cui si deduce che P è il punto medio del segmento DC come lo è I del segmento EF.
Ragionamento analogo vale per le coppie di triangoli simili KQB, KIF e KAQ, KEI in cui i segmenti QB, IF e AQ, EI sono in proporzione.
La retta KI taglia le basi del trapezio in parti uguali, nei loro punti medi.
Soluzione proposta da
Sara Vettori ed Helena Nocentini
Scuola Media “L. da Vinci" - Rufina (FI)
Prima risposta:
parte a) […]
parte b
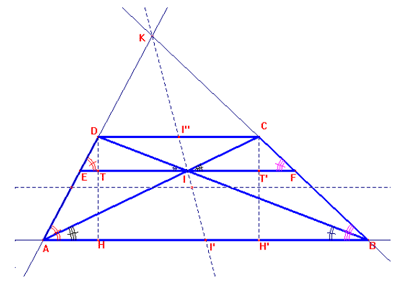
Consideriamo i triangoli KDC, KEF e KAB. Sono omotetici
tra di loro perché individuati da rette uscenti da un punto comune, K, e da
rette parallele che intersecano le rette sopra dette. [[Quindi]] gli angoli in
D,E e A sono uguali perché corrispondenti, formati dall’intersezione delle basi
DC, EF e AB, con il lato obliquo AD.
Stessa cosa vale per gli angoli in B, F e C, formati dall’intersezione delle
basi con il lato obliquo CB.
Chiamo I’ e I’’ i punti di intersezione delle basi AB e DC con la retta IK.
Per la similitudine stabilita [fra le coppie di triangoli KEF e KEI, KAB e KAI’,
e KDC e KDI’’] avremo:
EF : EI = AB : AI’ = DC : DI’’
Poiché al primo membro abbiamo un rapporto 2 : 1, tale rapporto varrà anche al
secondo e terzo membro. La retta IK quindi rappresenta la mediana del triangolo
KEF, ma anche di tutti i triangoli omotetici ad esso.
Seconda risposta:
parte a) […]
Generalizzazione:
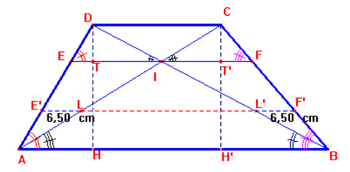
Risulta evidente dall’osservazione delle proporzioni [AB :
EI = DH : DT e AB : IF = DH’ : DT’ considerate nella prima parte] che ogni
parallela [alle basi] condotta per un punto qualsiasi [E’] di un lato obliquo
interseca le diagonali [e l’altro lato obliquo] individuando segmenti
congruenti, basi di una coppia di triangoli equivalenti [E’L’D, CLF’].
Perciò i segmenti individuati dall’intersezione di ogni parallela alle basi del
trapezio con un [[qualsiasi punto del]] lato obliquo e la rispettiva diagonale,
sono congruenti [E’L = L’F’].
Parte b) […]
| Home Page Cabri | Torna a FLATlandia | Archivi |