FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Gennaio 2002

a)  Costruire tre circonferenze di raggio 1 (uno) a due a due tangenti esternamente. Giustificare la costruzione.

b)  Indicati con A, B, C i punti di tangenza, considerare su ciascuna circonferenza il minore dei due archi ottenuti. Sia ABC il "triangolo curvilineo" delimitato da tali archi.
Determinare la posizione del centro e la lunghezza del raggio della circonferenza inscritta in ABC, motivando le risposte.

c)  Calcolare l'area del "triangolo curvilineo" ABC.

Commento

Abbiamo ricevuto diciotto risposte provenienti da dodici scuole (sei scuole medie inferiori e sei superiori). Ci e' pervenuta anche una risposta da una classe terza di un liceo scientifico, ma, come è scritto nel messaggio di presentazione del problema del mese, non possiamo più pubblicarla.

Le scuole che hanno partecipato sono:

• LG "Orazio" Roma RM due risposte
• SM "Panzacchi" Ozzano Emilia BO
• Istituto Comprensivo 2 Suzzara MN
• LS "E. Amaldi" Bitetto BA
• SM "Dalla Chiesa" S. Genesio PV
• ITI "B. Pascal" Cesena FC
• SM "Zanella" Roveredo in Piano PN
• ITI, LST "Berenini" Fidenza PR sei risposte
• Ist. Compr. "De Amicis" Busto Arsizio VA
• L.Linguistico "D. Alighieri" Padova PD
• LS "B. Pascal" Merano BZ
• SM "L. Da Vinci" Rufina FI

Nel problema proposto a Gennaio si chiedeva di costruire tre circonferenze di ugual raggio, a due a due tangenti, e di determinare il centro della circonferenza inscritta nel "triangolo curvilineo" da esse racchiuso. Si chiedeva inoltre di calcolare la misura del raggio della circonferenza inscritta e la misura dell'area di tale triangolo.

I quesiti posti non erano difficili e, proprio per questo, saremo più rigorosi nella valutazione dei vostri elaborati.

Pochi sono gli errori riscontrati: il calcolo del raggio della circonferenza inscritta, in due risposte, e una giustificazione alla prima costruzione in un'altra risposta.

Nella maggior parte delle soluzioni abbiamo però trovato spesso incomplete e/o imprecise le giustificazioni alle costruzioni. Probabilmente l'immediatezza delle proprietà da rilevare e dei calcoli da eseguire ha contribuito a rendere le vostre risposte un po' precipitose.

Riteniamo necessario fare alcune osservazioni:

• ribadiamo ancora una volta che è opportuno descrivere le costruzioni, ma, soprattutto per i ragazzi di scuola superiore, è doveroso giustificarle:
• quando si assegna una generica unità di misura non è necessario attribuirle una estensione (il centimetro o altro);
• ad una unità di misura non si può assegnare un valore numerico diverso da "uno", qualsiasi sia la grandezza che la rappresenta;
• nei calcoli con risultati decimali non finiti è preferibile esprimere tali risultati mediante simboli (pi greco, radice quadrata, 1/3 ...), soprattutto da parte dei ragazzi di scuola superiore;
• se si opta per il calcolo con numeri decimali approssimati, è opportuno usare almeno due cifre decimali.

Riteniamo infine doveroso da parte nostra fare un elogio ai ragazzi delle scuole medie inferiori in quanto si sono dimostrati più attenti, sia nelle descrizioni sia nelle motivazioni, di molti loro compagni più grandi.

Il problema di questo mese non si prestava a diversi percorsi di risoluzione, quindi presenteremo una sola risposta per ciascuno dei due ordini di scuola.
Per la scuola media inferiore abbiamo scelto quella dell'Istituto Comprensivo di Suzzara e, per le scuole superiori, la risposta di Studer Alessandro dell'ITI "Berenini" di Fidenza.
Come di consueto inseriremo le nostre correzioni o osservazioni fra parentesi quadra.

Soluzioni

Soluzione proposta da
Feroldi Fabio, Rovesti Pietro, Di Giacomo Ascanio
classe 3C  -  Istituto Comprensivo 2 - Suzzara (MN)

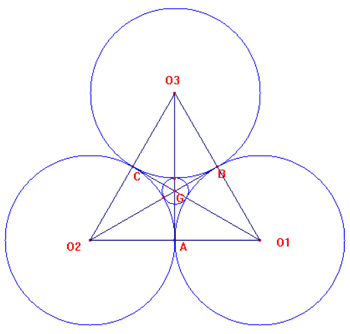
a) Disegniamo un triangolo equilatero di lato 2 [e vertici O1O2O3]; disegniamo le circonferenze con centro nei vertici del triangolo e passanti ciascuna per i punti medi di 2 lati consecutivi e perciò di raggio 1.

Tali circonferenze sono tangenti esternamente a due a due, infatti :

O1O2= 2= R1+R2 O1O3= 2= R1+R3 O2O3= 2= R2+R3

Cioè la distanza dei centri è sempre uguale alla somma dei raggi.

b) Il centro del cerchio inscritto nel “triangolo curvilineo” ABC è determinato dal punto G incontro delle mediane del triangolo O1O2O3, infatti:

G è equidistante dai vertici del triangolo e perciò è equidistante dalle 3 circonferenze; tale distanza è il raggio del cerchio inscritto.

Calcoliamo la lunghezza del raggio:

O1C = sqr (22-12) =1,73

O1G= 1,73:3*2 = 1,16

Raggio = O1G-R1=1,16-1= 0,16

c) L’area del triangolo curvilineo ABC può essere calcolata togliendo dall’area del triangolo O1O2O3 i tre settori circolari interni al triangolo di ampiezza 60° ciascuno.

Area triangolo = 2*1,73 :2=1,73

Area settori =(1*1*3,14):6*3= 1,57

Area triangolo curvilineo =1,73-1,57= 0,16

Soluzione proposta da
Alessandro Studer
2°B St.  - ITIS Berenini - Fidenza (PR)

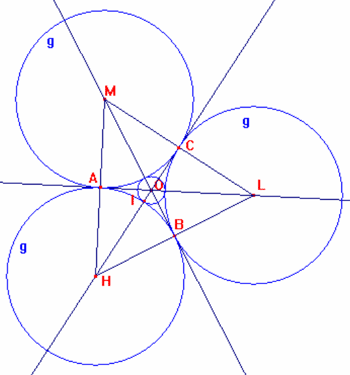
a) I centri delle tre circonferenze devono coincidere con i vertici di un triangolo equilatero di lato 2 (due) perché due circonferenze sono tangenti quando la distanza tra i centri è uguale alla somma dei due raggi e il raggio del cerchio deve essere congruente alla metà del lato del triangolo equilatero.

Il posizionamento dei centri sui vertici di un triangolo equilatero soddisfa questa condizione per il fatto che i lati del triangolo sono uguali.

b) La posizione del centro della circonferenza inscritta nel triangolo curvilineo ABC è collocata nell’intersezione delle altezze, mediane e bisettrici cioè nel circocentro, baricentro e ortocentro del triangolo equilatero HLM.

Questo perché la mediana, l’altezza e la bisettrice del triangolo HLM lo sono anche nel triangolo curvilineo ABC [essendo i tre archi congruenti fra loro].

La lunghezza del raggio della circonferenza iscritta in ABC risulterà essere uguale alla distanza tra il vertice e l’ortocentro (HO) meno il raggio del cerchio (HI).

HO è pari a 2/3 di HC perché il baricentro O divide la mediana HC in due parti una il doppio dell’altra.

HC si trova applicando il Teorema di Pitagora.

HC = sqrt(2^2-1^2) = sqrt(3)

HO = 2/3*sqrt(3)

HI = 1

OI = HO-HI = (2/3*sqrt(3))-1=0.15

c) L’area del triangolo ABC viene calcolata come differenza dell’area del triangolo HLM meno la somma dei tre settori circolari HBA; LBC; MAC che essendo ciascuno 1/6 di cerchio (ognuno [ogni angolo al centro] misura 60°, perché angolo del triangolo equilatero) danno luogo complessivamente ad un totale di 1/2 cerchio.

Area HLM = (HC*ML)/2=sqrt(3)

Area semicerchio “g” = 1/2 (HI^2)*(pi greco) = 1/2*(pi greco)

Area ABC = A(HLM)-A(“1/2 g”) = sqrt(3)- 1/2*(pi greco)

| Home Page Cabri | Torna a FLATlandia | Archivi |