 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Dicembre 2001
a) Per distanza di un punto da una
circonferenza si intende il minimo segmento che congiunge quel punto con
un punto della circonferenza.
Come costruire tale distanza?
Giustificare la risposta.
b) Dati ora quattro punti in uno stesso
piano, non tutti sulla stessa retta, disegnare una circonferenza
equidistante da essi.
Motivare la costruzione.
c) Il problema proposto in (b) ha un'unica soluzione?
Commento
Abbiamo ricevuto in tutto undici risposte provenienti da
dieci scuole. Per quanto ci risulta, solo due scuole medie inferiori hanno
tentato l'impresa.
Il problema di Dicembre proponeva una riflessione sul concetto di distanza (fra
un punto ed una circonferenza) e richiedeva un "pizzico" di fantasia per
costruire una circonferenza equidistante da quattro punti. Si chiedeva poi, per
stimolare la ricerca di eventuali altre soluzioni, se fosse l'unica soluzione
possibile.
Nelle risposte pervenute sono stati individuati due percorsi per la costruzione
della suddetta circonferenza e, per ciascuno di essi, qualcuno ha indagato su
quante soluzioni fossero possibili in base alla scelta dei quattro punti.
In nessuna risposta sono stati individuati tutti i casi che potevano
presentarsi, ma ciò non era richiesto.
Sono state considerate complete le soluzioni in cui risulta:
Poche sono le risposte che soddisfano tutti questi
requisiti; si sono riscontrate infatti varie carenze e/o errori nella prima e
terza parte. Quasi tutti i partecipanti hanno fornito una costruzione
accettabile nella seconda parte: la maggior parte ha considerato la
circonferenza per tre dei punti dati e dimezzato la distanza del quarto da tale
circonferenza, alcuni invece hanno considerato due circonferenze concentriche
ciascuna per due dei punti assegnati e dimezzato la loro distanza.
A corredo del commento verrà presentata, sul sito di FLATlandia, a cura del
comitato, una serie di figure che illustrano varie possibilità di soluzione del
quesito (b).
Le scuole che hanno partecipato sono:
Si è convenuto di presentare le seguenti soluzioni:
NOTA: Le correzioni al testo o i commenti sono scritti in parentesi quadra. Sono racchiuse in doppia parentesi quadra le parti ritenute superflue.
SOLUZIONI
 |
 |
 |
|
Si possono ottenere
quattro circonferenze distinte fornite dalle terne di punti |
In questo
caso si ottengono tre circonferenze distinte fornite dalle terne di punti (A,B,C),(A,D,C),(B,D,C) |
Si hanno infinite soluzioni: tutte le circonferenze concentriche con quella per i quattro punti |
 |
 |
 |
|
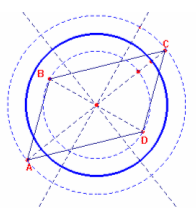
Si hanno tre distinte
circonferenze fornite dalle coppie di segmenti |
Se AD//BC si hanno due sole circonferenze fornite dalle coppie di segmenti (AB,CD), (AC,BD) | Se AB//CD e AD//BC si ha una sola soluzione data dalla coppia di segmenti (AC,BD) |
Soluzione proposta da un gruppo di
alunni classe seconda
liceo scientifico tecnologico ITI "Cesaris" - Casalpusterlengo (LO)
a)
Consideriamo una circonferenza c di centro O e un punto P ad essa esterno.
Congiungiamo P con O. Il segmento PO interseca la circonferenza in H. PH è la
distanza di P da c .
Infatti congiungendo P con un qualsiasi altro punto R della circonferenza, PH <
PR, utilizzando il teorema che dice "in un triangolo, la differenza di due lati
è minore del terzo lato e applicandolo al triangolo PRO si ha
PO - OR < PR cioè, poiché OR = OH, PH < PR
Se il punto P fosse interno alla circonferenza, la sua distanza è data dal segmento PH, dove H è l'intersezione tra c e il prolungamento, oltre P, del raggio passante per P. In questo caso preso un qualsiasi altro punto R di c e ragionando sul triangolo ORP si ottiene ancora
PR > RO - PO = HO - PO = HP.
Se il punto P appartenesse alla circonferenza la sua distanza sarebbe nulla.
b)
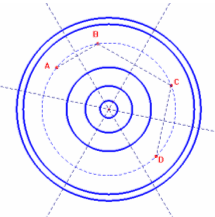
Se i quattro punti appartenessero ad una circonferenza, questa sarebbe la
[una delle infinite] circonferenza cercata (da cui distano tutti zero) [tutte le
circonferenze concentriche con questa sono una soluzione].
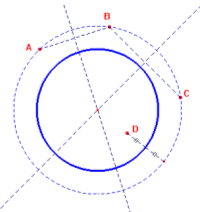
[Altrimenti] costruiamo la circonferenza c di centro O passante per 3 dei quattro punti. Il quarto punto D potrebbe essere interno o esterno. La circonferenza equidistante dai quattro punti è ovviamente quella di centro O e di raggio uguale alla media aritmetica tra il raggio di c e la misura OP [(r+OP)/2].
Dati i quattro punti questo ragionamento si può rifare per ogni scelta dei tre iniziali e quindi ci sono 4 possibili circonferenze.
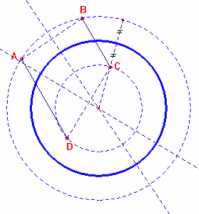
Si possono anche costruire circonferenze equidistanti dai quattro punti e che ne lascino due interni e due esterni.
Si osserva che se due punti sono esterni (o interni) alla circonferenza ed equidistanti da essa le loro distanze dal centro O devono essere uguali per quanto visto nel punto a).
Costruiamo una delle possibili soluzioni.
Il centro O della circonferenza cercata dovrà appartenere quindi all'asse del segmento AD e anche all'asse del segmento BC. Quindi il centro O si trova nella loro intersezione Il raggio della circonferenza cercata è la media aritmetica dei raggi delle circonferenze di centro O e passanti rispettivamente per A e D.
In questo modo la circonferenza è equidistante dai quattro punti A, B, C, D. Potrei rifare il ragionamento prendendo le coppie A,C e B,D oppure le coppie A,B e C,D
c)
Il problema non ha un'unica soluzione, come visto nel punto b)
Soluzione proposta dalla Classe 2 TB
Liceo Scientifico "N. Tron" - Schio (VI)
[...]
DOMANDA B
DIMOSTRAZIONE
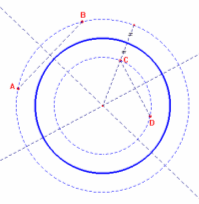
1. esso è appartenente alla circonferenza appena costruita: le circonferenze equidistanti ai 4 punti sono infinite, cioè tutte le circonferenze concentriche a quella di partenza.
2. esso è interno o esterno alla circonferenza costruita:
DOMANDA C
DIMOSTRAZIONE
Soluzione proposta dagli Alunni:
Agnes, Amodeo, Ariodante, Braschi, Izzo, Pozzato
Classe 3°P - Scuola Media “C.A. Dalla Chiesa” – San Genesio ed Uniti (PV)
a)
-P esterno alla circonferenza:
Congiungendo P con O centro della circonferenza otteniamo il segmento PO. Chiamiamo A il punto di intersezione tra il segmento e la circonferenza. Il segmento PA è la distanza di P dalla circonferenza.
-P interno alla circonferenza:
Tracciamo il raggio passante per P. Il punto di intersezione del raggio con la circonferenza lo chiamiamo A. La distanza è PA.
PA è il segmento di lunghezza minima perché se prendiamo un altro punto K sulla circonferenza e congiungiamo i punti P, O, K si ottiene il triangolo PKO; se PK fosse uguale a PA , OK e PK sarebbero sovrapposti a PO e se PK<PA non si sarebbe potuto formare il triangolo [giustificazione non del tutto rigorosa ed incompleta].
b)
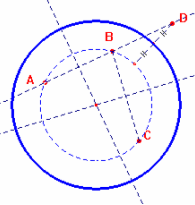
Chiamiamo A, B, C, D quattro punti non allineati del piano.
Consideriamo il triangolo ABC. Il punto d’intersezione degli assi dei segmenti AB e AC è il centro della circonferenza circoscritta al triangolo ABC, che chiamiamo O.
Tracciamo il segmento che congiunge O con D e chiamiamo N
il punto di intersezione con la circonferenza.
Troviamo il punto medio M del segmento ND.
Tracciamo la circonferenza di centro O con apertura OM. Questa è la
circonferenza che cercavamo, perché i punti A, B,C distano dalla circonferenza
NM e il punto D dista dalla circonferenza MD, poiché NM=MD i punti sono ad ugual
distanza.
Nel caso in cui D sia interno alla circonferenza passante per A,B e C, la costruzione è la stessa.
[...]
| Home Page Cabri | Torna a FLATlandia | Archivi |