 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Aprile 2002
Motivare le risposte.
 |
 |
 |
Scuola Media Statale “Bergamaschi” Per meglio capire le figure nello
spazio, |
Commento
Nel mese di Aprile abbiamo ricevuto quattro risposte due delle quali dalla scuola media inferiore. Forse i ragazzi che ci seguono non amano molto i quesiti sulla geometria dello spazio oppure in questo periodo sono maggiormente impegnati in altre attività. Le scuole che hanno partecipato sono:
Il problema proponeva tre quesiti sul concetto di luogo
geometrico di punti nello spazio. Nelle risposte pervenute sono stati affrontati
tutti i quesiti, ma nessuna di esse è da ritenersi pienamente soddisfacente.
Nella prima e seconda parte del problema, anche nel caso in cui sia stato
correttamente individuato il luogo richiesto, non è stata dimostrata la sua
unicità. Vi ricordiamo che si definisce LUOGO l'insieme di TUTTI e SOLI i punti
che godono di una data proprietà.
Nella terza parte, in una sola risposta ci si è preoccupati di dimostrare la
complanarità delle due rette che poi individueranno il punto che rappresenta il
luogo richiesto; anche in questo caso però la risposta non è esauriente. Inoltre
nessuno dei partecipanti ha notato che tale punto è il centro della sfera
passante per i quattro punti assegnati. In analogia con la circonferenza nel
piano, esiste ed è unica la sfera che passa per quattro punti, a tre a tre non
complanari.
Abbiamo stabilito di presentare ugualmente le parti di soluzioni ritenute più
valide accompagnate da nostre osservazioni o completamenti, racchiuse, come di
solito, in parentesi quadre.
Ci dispiace per lo studente di L'Aquila del cui lavoro non possiamo riportare
alcuna parte in quanto, come abbiamo più volte ribadito, le risposte dei ragazzi
delle scuole superiori debbono essere pienamente giustificate.
Riporteremo dunque le soluzioni:
NOTA: come al solito, le correzioni e i commenti sono inseriti in parentesi quadra. Le parti superflue o quelle mancanti in doppia parentesi quadra.
SOLUZIONI
Soluzione proposta da:
Classe 2 B - Liceo Scientifico "E. Amaldi" - Bitetto BA
a)
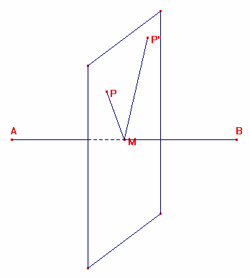 fig. 1
fig. 1
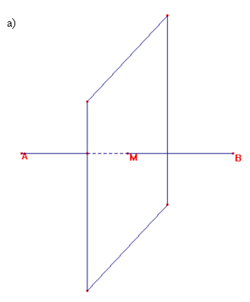
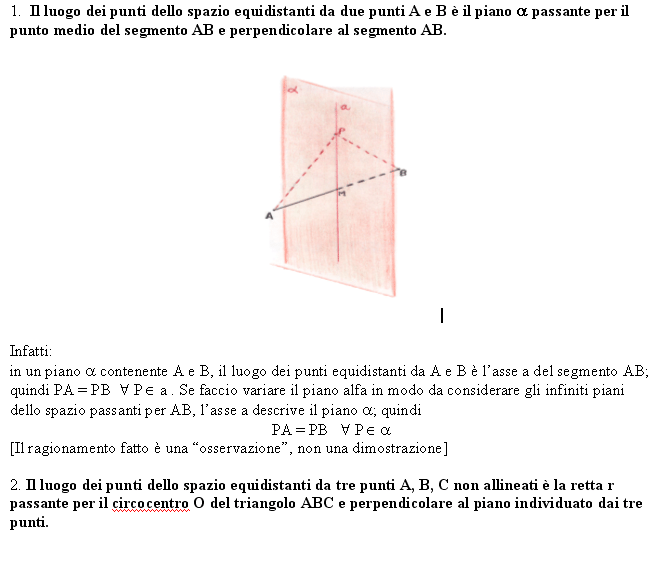
L'insieme dei punti nello spazio equidistanti
da A e B, distinti, è il piano perpendicolare, nel punto medio M del segmento AB,
al segmento stesso AB.
Infatti (vedi fig.1) se P è un punto di tale piano, PA e PB sono ipotenuse dei
triangoli rettangoli PMA e PMB, ed essendo MA=MB, sarà PA=PB.
[[NOTA: occorre ora dimostrare che i punti di tale piano "p" sono gli unici
punti dello spazio equidistanti da A e B.
Supponiamo che esista un altro punto Q, non appartenente a "p", tale che sia QA=QB.
Il triangolo QAB sarà allora isoscele su AB, risulterà QM perpendicolare ad AB e
quindi appartenente ad un piano "q" perpendicolare ad AB in M.
Poiché non possono esistere due piani distinti perpendicolari ad una retta in un
suo punto sarà "p"="q"]].
b)
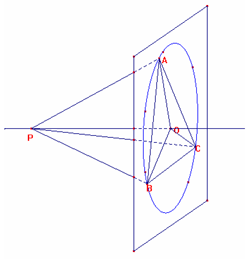 fig. 2
fig. 2
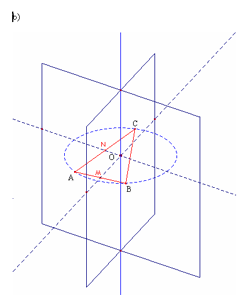
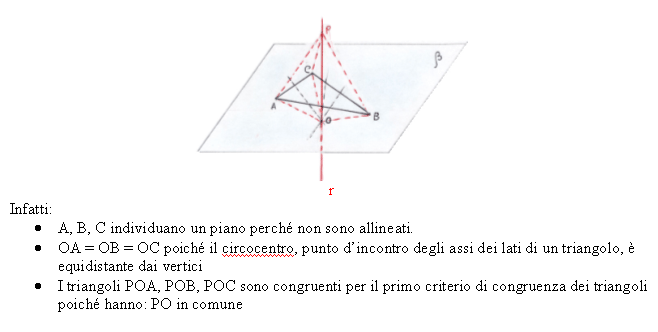
Nel secondo caso, i tre punti non allineati formano un
triangolo ABC. Sul piano da essi determinato, costruiamo il suo circocentro O
(in fig.2, la conica-ellisse simula la circonferenza circoscritta ed i vertici
A, B, C risultano equidistanti da O, cioè AO=BO=CO).
L'insieme dei punti nello spazio, equidistanti da A, B e C è la retta
perpendicolare nel circocentro O del triangolo ABC al piano del triangolo.
Infatti, se P è un qualsiasi punto su tale perpendicolare le tre distanze PA, PB
e PC sono tutte uguali tra loro essendo ipotenuse dei triangoli rettangoli PAO,
PBO e PCO (infatti se una retta è perpendicolare ad un piano, ogni retta del
piano passante per l'intersezione è perpendicolare alla retta) ed essendo AO=BO=CO.
[[NOTA: I punti di tale retta sono i soli equidistanti da A, B e C essendo essa
intersezione dei tre piani perpendicolari al lati del triangolo ABC nei loro
punti medi]].
c) [[...]]
Soluzione proposta da:
Paolo Agnes - classe III P - SM "C. A. Dalla Chiesa", S. Genesio
a. [[...]]
b. [[...]]
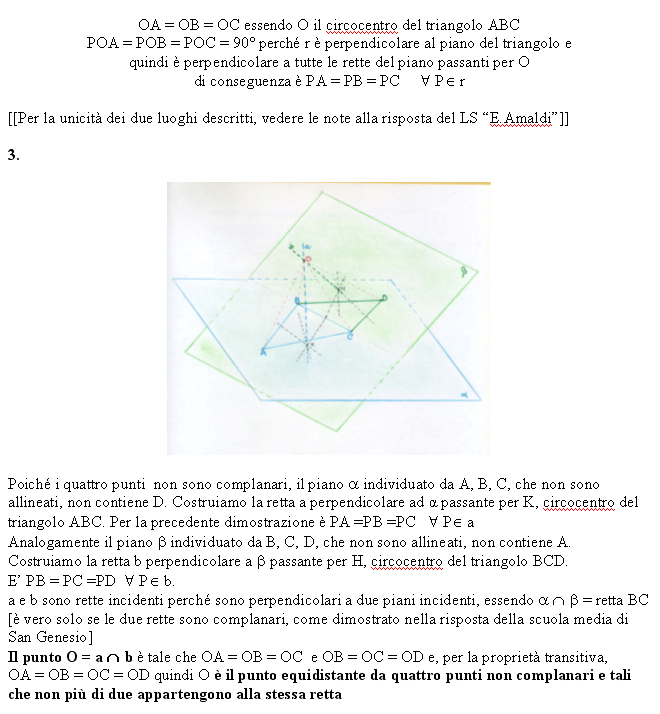
c. Presi quattro punti non complanari A, B, C e D
considero tre punti per volta. Questi individuano un piano. Sul piano ABC
considero il triangolo ABC e trovo il suo ortocentro [circocentro], che chiamo
Q.
Chiamo "s" la retta passante per Q e perpendicolare al piano.
Sul piano ABD considero gli assi di AB e BD e trovo l'ortocentro [circocentro]
di ABD. Chiamo P il punto ottenuto, e la retta perpendicolare al piano e
passante per esso la chiamo "t".
Considero il piano individuato dalla retta "s" e dall'asse del segmento AB
passante per Q. Questo piano "alfa" è perpendicolare ad AB e passa per il suo
punto medio.
Considero ora il piano individuato dalla retta "t" e dall'asse di AB passante
per P. Anche questo piano "beta" è perpendicolare ad AB e passa per il suo punto
medio.
Pertanto i due piani "alfa" e "beta" coincidono essendo perpendicolari nello
stesso punto allo stesso segmento. Le rette "t" e "s" sono quindi complanari [[e
incidenti essendo esse perpendicolari, nello stesso piano, a due rette che si
incontrano, gli assi di AB passanti uno per P e uno per Q]].
Il punto O, intersezione di "t" e "s" è quindi equidistante da A, B, C e D nello spazio.
Soluzione proposta da:
Davide Montalbano, Ilaria Andena, Teresa Pedrini, Sarah Taha
Classe 3M - Scuola Media Statale “Bergamaschi”, Torrevecchia Pia
| Home Page Cabri | Torna a FLATlandia | Archivi |