 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Ottobre 2000
Il testo del problema:
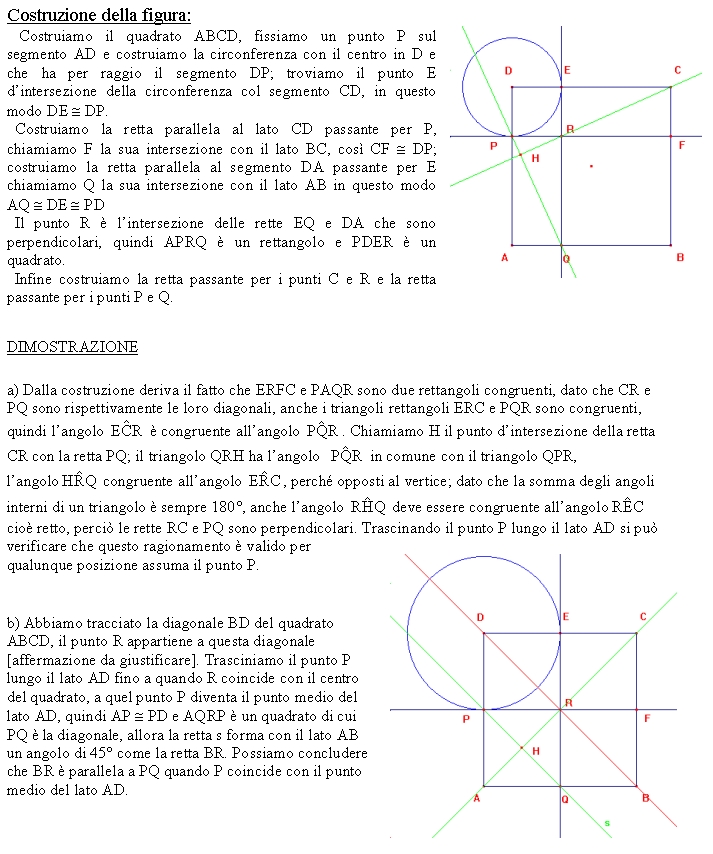
E' dato un quadrato ABCD. Considerare sul lato AD un punto P e sul lato AB un punto Q tale che sia AQ congruente a DP. Disegnare il rettangolo AQRP.
a) Dimostrare che la retta CR è perpendicolare
alla retta PQ.
b) Determinare la posizione del punto P affinché la retta BR sia
parallela alla retta PQ. Motivare la risposta.
Commento
Abbiamo ricevuto ventitre risposte provenienti da diciannove scuole, fra le quali quattro scuole medie e una scuola elementare. E' giunta una ulteriore risposta da una associazione culturale di Rosario, Argentina, purtroppo illeggibile. Abbiamo replicato al messaggio, ma non siamo riusciti a stabilire alcun contatto con quell'Istituto.
Le scuole che hanno partecipato sono:
Nel problema di questo mese si trattava di indagare la posizione reciproca di
due rette all'interno di un quadrato in una situazione generica, nella prima
parte, e quella di due rette in un caso particolare, nella seconda parte.
Alcune delle risposte pervenute non sono accettabili: in una è errata la figura
e quindi modificato il percorso della dimostrazione; in altre si è tentata una
dimostrazione senza tener conto di tutte le ipotesi del problema nella prima
parte; una ha invece modificato un dato del problema nella seconda parte.
In molte altre risposte il problema è stato risolto in modo impreciso o nella
descrizione della figura o nella esposizione; qualcuno si è dilungato
eccessivamente nelle giustificazioni, qualcuno e' invece stato troppo conciso a
scapito della completezza.
Nella maggior parte delle risposte il punto a) è stato dimostrato ricorrendo alla congruenza dei triangoli rettangoli sfruttando quindi gli angoli complementari. Qualcuno ha tentato approcci diversi e interessanti (rotazione, similitudine) senza riuscire a dare però una giustificazione esauriente.
Il punto b), apparentemente molto semplice, è stato affrontato in generale in due modi: chi ha fatto una dimostrazione diretta, a partire dalle ipotesi, ha individuato l'esistenza ma non la unicità del punto trovato; chi invece ha preso in esame la tesi per scoprire le condizioni che la determinano ha dimostrato solo la unicità del punto richiesto.
Immagine Animata Cabrijava
Realizzata dall'I.T.I. "Berenini" di Fidenza (PR)
Soluzione proposta da
Daniele Urzì, classe 3a B, liceo scientifico "G.Galilei" - Catania
a) Sia V l'intersezione tra le rette CR e PQ. Si prolunghi QR fino ad
incontrare DC nel punto T. Considerando le rette parallele DC e PR, tagliate
dalla trasversale CV, gli angoli TCR e PRV sono congruenti perché
corrispondenti. Poiché il quadrilatero PRTD ha gli angoli interni retti è un
rettangolo ed è semplice dimostrare che è anche un quadrato. Altrettanto
facilmente si dimostra che è TC congruente a RQ. Quindi i triangoli rettangoli
TRC e PRQ sono congruenti poiché hanno i cateti ordinatamente congruenti. In
particolare si ha [l'angolo] QPR congruente a TRC. In riferimento al triangolo
PVR, siccome gli angoli RPV e VRP sono complementari, l'angolo PVR è retto.
Così è dimostrato che le rette PQ e CR sono perpendicolari.
Nota:
Nel caso in cui P coincida con A o con D la proprietà del quesito a) è
verificata, poiché PQ e CR coincideranno alternativamente con due lati
consecutivi del quadrato.
Se P appartiene al prolungamento di AD dalla parte di D, la proprietà suddetta
si verifica considerando Q sul prolungamento di AB dalla parte di A. Se P giace
invece sul prolungamento di AD dalla parte di A, Q deve essere preso sul
prolungamento di AB dalla parte di B.
Soluzione proposta da
Stefania Bisogno, Classe 2 C Liceo Scientifico "Scorza" - Cosenza
DIMOSTRAZIONE DEL SECONDO PUNTO
Per dimostrare il secondo punto, sono partita già dal fatto che le rette BR
e PQ sono parallele. Così, si viene a formare il parallelogramma PQBR; pertanto
i lati PR e QB sono uguali, perché lati opposti di un parallelogramma. Allora,
dato che AQ=PR=PD, come precedentemente dimostrato, QB è uguale ad AQ e DP è
uguale ad AP: il punto P (così come il punto Q) è il punto medio del lato AD.
In tal modo, si è dimostrato che le due rette PQ e BR sono parallele solo se il
punto P coincide con il punto medio del lato AD.
Soluzione proposta da
Massimiliano Capecchi e Maddalena Pazzi
Classe 3a C Scuola Media "L. da Vinci" - Rufina (FI)
2. Considero la retta BR: essa è, nella mia figura, diagonale del quadrato
RQBK [K e' il punto di intersezione fra la retta PR e il lato CB] e quindi bisettrice
dell'angolo QBK. Nel rettangolo AQRP, viceversa, la retta QP è diagonale del
rettangolo medesimo e non è, quindi, bisettrice dell'angolo.
Solo quando il punto P è punto medio del lato AD, il quadrato ABCD sarà diviso
in 4 quadrati di cui le due rette PQ e BR saranno bisettrici e quindi tra loro
parallele (condotte ambedue dal vertice più in alto a destra a quello più in
basso a sinistra). In questa posizione il punto R coincide con il centro della
figura.
Soluzione proposta da
un gruppo di alunni della classe 3C Scuola Media L.Orsi di Novellara (RE)
| Home Page Cabri | Torna a FLATlandia | Archivi |