 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Novembre 2000
Il testo del problema:
Siano r ed s due rette incidenti in K e sia A un punto non appartenente ad esse.
a) Costruire un triangolo ABC in modo che le rette r ed s siano gli assi di due suoi lati. Quante sono le soluzioni possibili?
b) Se il punto A appartiene ad una delle due rette e' ancora possibile effettuare la costruzione? Se sì, quante soluzioni esistono?
Motivare le risposte.
Abbiamo ricevuto venti risposte provenienti da diciassette
scuole di cui tre scuole medie inferiori.
Ecco l'elenco delle scuole che hanno partecipato in questo mese:
Il problema proposto in questo mese chiedeva di costruire
un triangolo dati due suoi assi, prima in un caso generico, poi in una
situazione particolare, e di esaminare le varie possibilità di risoluzione.
Tre delle risoluzioni pervenute non sono accettabili perché largamente carenti;
sei risposte risultano invece incomplete o nella prima o nella seconda parte.
In tutte le rimanenti risposte il problema è stato risolto in modo
soddisfacente ricorrendo o alla simmetria assiale, nella maggior parte di esse,
o alla proprietà delle corde (considerando la circonferenza circoscritta ai
triangoli da costruire).
Sono state individuate le soluzioni generali, ma non sono stati indagati tutti i
casi particolari, soprattutto nella prima parte.
Si rendono necessarie alcune osservazioni:
- "Siano r ed s due rette incidenti …e sia A un punto…" NON
SIGNIFICA risolvere il problema proposto per ogni coppia di rette e per ogni
punto, ma, una volta fissate due rette generiche e un punto qualsiasi (non
appartenente o appartenente ad esse), determinare tutte le possibili soluzioni;
successivamente si possono esaminare posizioni particolari delle rette e/o del
punto.
- Nessuno ha messo in evidenza che le costruzioni individuate nella prima parte
sono le uniche possibili.
- Dopo aver individuato la soluzione generale e' opportuno esaminare anche le
posizioni particolari per verificare se rientrano nel caso generale o se
producono situazioni nuove, che saranno quindi da evidenziare.
Fra le risposte accolte, abbiamo concordato di presentare quella del Liceo scientifico "G.Galilei" di Bitonto completata da una osservazione di Daniele Urzì del Liceo Scientifico "G.Galilei" di Catania. Per la scuola media inferiore, riportiamo quella della SM di Rufina, anche se non prende in esame i casi particolari.
|
|
|
|
|
|
NOTA: Le correzioni o i commenti al testo sono riportate in parentesi quadra.
Soluzione proposta da:
2 E liceo scientifico "G. Galilei" Bitonto (BA)
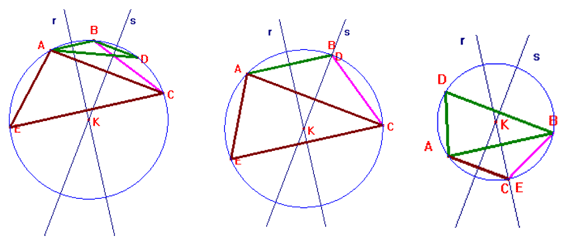
a) Indichiamo con sr la simmetria assiale rispetto
ad r e con ss la simmetria assiale rispetto all'asse s.
Sia B=sr(A) e C=ss(A), ABC è un primo triangolo di vertice A avente r come asse
di AB e s come asse di AC.
Sia D=ss(B), ABD è un secondo triangolo avente r come asse di AB e s asse di BD.
Sia E=sr(C), ACE è un terzo triangolo avente r come asse di CE e s come asse di
AC.
Per tutti questi triangoli K è il circocentro, infatti la
circonferenza di centro K e passante per A, passa anche per i punti B, C, D, E.
Dunque sono possibili in generale tre soluzioni.
Nel caso particolare che B cada su s, si ha che B=D e le soluzioni scendono a
due in quanto il triangolo ABD degenera in un segmento (vedi fig.2) [e il
triangolo ABC diventa isoscele]
Analogo discorso se C cade su r [C=E] (vedi fig. 3) [Manca
il caso in cui la soluzione è una sola, cioè un triangolo equilatero: si ha
quando A e' sulla bisettrice dell'angolo ottuso formato da r ed s e l'angolo
acuto misura 60°]
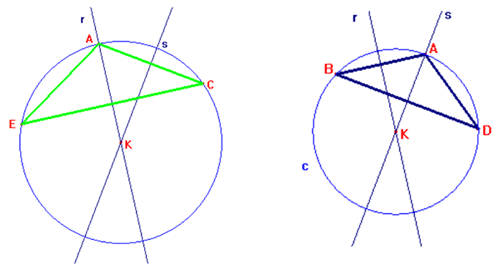
b) Se A appartiene a una delle due rette, la
soluzione è unica e si tratta del triangolo isoscele ACE (terza costruzione),
nel caso A appartenga a r o del triangolo ABD (seconda costruzione) nel caso che
A stia su s. I triangoli ACE e ABD sono isosceli perché dotati di un asse di
simmetria.
Infatti in questi casi particolari delle tre costruzioni del punto a) solo una
si può effettuare essendo A fisso [punto unito nella simmetria assiale]
rispetto a r o ad s.
Soluzione proposta da:
Daniele Urzì, classe III B liceo scientifico statale
"G.Galilei" (CT)
[...]
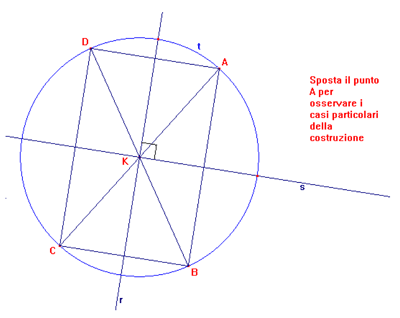
Se r e s sono perpendicolari basta [nel punto a)] considerare il rettangolo di
vertici A e i suoi simmetrici rispetto ad r, s, K e tracciare le diagonali:
tutti i triangoli rettangoli di vertice A sono quelli richiesti.
Quando invece A appartiene ad r o ad s e queste sono perpendicolari il triangolo
[il rettangolo] degenera sempre in un segmento e quindi il problema non ammette
soluzione.
Soluzione proposta da:
Massimiliano Bavecchi, III C SM
"Leonardo da Vinci" Rufina (FI)
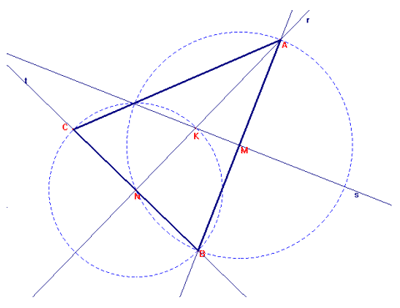
a) Ricordando che l'asse di un segmento è la retta
perpendicolare condotta per il suo punto medio, parto da A e traccio le
perpendicolari t ad r e w ad s, che intersecano rispettivamente in M ed in N i
due assi. Con il "Compasso" punto in M e con apertura AM, disegno una
circonferenza.
Individuo così un punto di intersezione tra la circonferenza e la retta t che
chiamo B. Nello stesso modo, con il "Compasso" punto in N e con
apertura NA traccio la circonferenza. Nel punto di intersezione di questa
circonferenza con la retta w individuo il vertice C del triangolo. Con l'opzione
triangolo traccio il triangolo ABC individuato mediante i punti così
determinati.
E' possibile effettuare tre costruzioni di triangoli aventi come assi le rette r
ed s, incidenti in K, partendo da un punto A esterno ad esse.
- Nella prima:
A va in B mediante r, A va in C mediante s [vedi costruzione precedente].
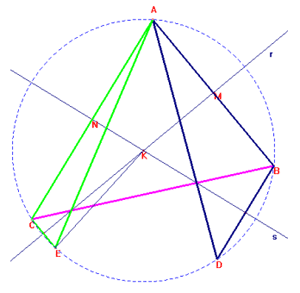
- Nella seconda:
A va in B mediante r, B va in D mediante s [con costruzione analoga].
- Nella terza:
A va in C mediante s, C va in E mediante r [come sopra].
b) Se il punto A appartiene ad una delle due
rette e' ancora possibile effettuare una sola costruzione, tracciando una
perpendicolare da A sull'altra retta e ancora applicando il procedimento
precedente.
Immagino il punto A sulla retta r. Chiamo M il punto di intersezione tra la
retta s e la perpendicolare ad essa w, passante per A.
Con centro in M e apertura del compasso AM trovo il punto B dato
dall'intersezione di w con la circonferenza. Una volta trovato B, traccio la
perpendicolare t da B alla retta r. Nell'intersezione di t ed r si troverà il
punto N. Punto poi in N con apertura BN, e traccio la circonferenza di diametro
BC (l'intersezione della circonferenza con la retta t individua il punto C).
Il triangolo ABC è l'unico che posso costruire; infatti il simmetrico di A
rispetto alla retta r è un punto che coincide con A stesso.
| Home Page Cabri | Torna a FLATlandia | Archivi |