FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Maggio 2001

Il testo del problema:

a) Sono dati un rettangolo ABCD di base AB e altezza AD ed un punto E situato sulla semiretta di origine A contenente B.
Costruire il rettangolo AEFG, con A e F vertici opposti, equivalente ad ABCD e situato dalla stessa parte di ABCD rispetto alla retta AE. Giustificare la costruzione.

b) Quale figura descrive il punto F al variare di E sulla semiretta AB?
Quale "legge" matematica è rappresentata da tale figura?

c) Siano r e t due semirette di origine O. Riportare su r i segmenti OS e OP, congruenti rispettivamente ai lati AB e AD del rettangolo assegnato, e su t i segmenti OR e OQ, congruenti rispettivamente ai lati AG e AE del rettangolo costruito in a).
Dimostrare che i punti S, P, Q, R appartengono ad una stessa circonferenza.

Commento

Abbiamo ricevuto tre risposte; ci hanno seguiti fino all'ultimo problema di questo anno scolastico due scuole superiori ed una scuola media inferiore:

• Scuola Media di Roveredo in Piano (PN)
• LS "E. Amaldi" Bitetto (BA)
• LS "G. Galilei" Bitonto (BA)

Il problema di questo mese comprende due fasi di lavoro. Nella prima, punti a) e b), si giunge alla costruzione di un luogo geometrico, grafico della legge di proporzionalità inversa; nella seconda parte, punto c), si utilizza la proporzionalità inversa fra due coppie di segmenti per dimostrare l'appartenenza di quattro punti ad una stessa circonferenza.
Riconosciamo che il problema proposto non era semplice, soprattutto per i più piccoli.
Le risposte inviate dai ragazzi dei due licei sono complete e corrette, abbastanza simili nella prima fase si differenziano nettamente nella dimostrazione del punto c).
Nella risposta della scuola media inferiore, una seconda classe, si fornisce una costruzione interessante, anche se un po' laboriosa, del luogo richiesto. In essa si fa ricorso al secondo teorema di Euclide anziché utilizzare le proprietà dell'equivalenza. Questi ragazzi hanno tentato poi di dimostrare il quesito del punto c), documentandosi anche su questioni che esulano dal loro iter scolastico, ma hanno gettato la spugna ad un passo dalla conclusone.

Abbiamo stabilito di presentare  le tre soluzioni che ci sono pervenute, corredate dalle loro figure, inserendo nella risposta della scuola di Roveredo, con una nota, una possibile conclusione per il punto c).

NOTA: Le correzioni al testo o i commenti sono scritti in parentesi quadra. Sono racchiuse in doppia parentesi quadra le parti ritenute superflue.

Soluzione proposta da:
Classe 2B - Liceo "E.Amaldi" - Bitetto (BA) 

In riferimento alle figure allegate,

a) Dato il rettangolo ABCD, sulla semiretta AB prendiamo un punto E (a destra di B, o a sinistra) e lo congiungiamo con D.
Dal vertice B mandiamo la parallela alla retta DE e chiamiamo G l'intersezione di tale retta con la retta AD.
Il triangolo ABD, metà del rettangolo ABCD, è somma dei 2 triangoli ABG e BDG, ma tale triangolo BDG è equivalente a BEG (hanno la stessa base BG e altezze DH, EK congruenti perchè comprese tra 2 parallele); quindi ABD equivale ad ABG+BGE=AEG e pertanto ABCD equivale ad AEFG.

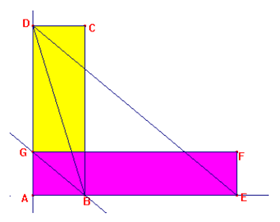
b) Il vertice F, al variare di E sulla semiretta AB, descrive un ramo di iperbole tangente alle semirette AB e AD (vedi file Fl2bAmaldi1.htm che abbiamo editato in CabriWeb con l'aiuto del nostro docente). Se indichiamo con b, h, x e y le misure di AB, AD, AE e AG, dall'equivalenza dei due rettangoli si ottiene y=bh/x legge della proporzionalità inversa.

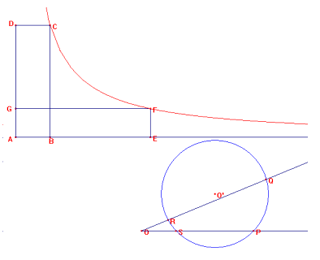
Riportiamo le misure b, h in OS e OP, le misure x, y in OQ e OR e consideriamo la circonferenza passante per i tre punti S, P, Q (circoscritta al triangolo SPQ, con O' intersezione dell'asse di SP con quello di PQ). Se indichiamo con R' l'intersezione della circonferenza con OQ, per il teorema delle secanti sarà OR'/OP=OS/OQ. Ma dall'equivalenza precedente y=bh/x diventa OR/OP=OS/OQ e per l'unicità della 4ª proporzionale otteniamo infine OR'=OR. Pertanto i quattro vertici S,P,Q,R appartengono alla stessa circonferenza.

Soluzione proposta da:
Classe 2E - Liceo scientifico "G. Galilei" Bitonto (BA)

a) Disegnato il rettangolo ABCD di base AB e altezza AD e preso il punto E sulla semiretta AB , per ottenere il rettangolo AEFG equivalente ad ABCD eseguiamo le seguenti costruzioni:

1. Si costruisce il triangolo ABN equiesteso ad ABCD avendo la stessa base e altezza AN=2AD;
2. Si congiunge E con N e si traccia per B la retta parallela a NE che incontra la semiretta AD in M. Si è ottenuto il triangolo AEM equiesteso ad ABN perché somma di triangoli equiestesi, infatti AEM=ANE+NEM, ABN=ANE+EBN con ANE parte comune e NEM equiv. EBN in quanto triangoli con la stessa base NE e stessa altezza perché compresi nella stessa striscia di piano delimitata dalle rette parallele NE e MB.
3. Si costruisce il rettangolo AEFG di base AE e altezza AG=1/2AM, equivalente ad AEM. Per la proprietà transitiva dell'equiestensione si ha che ABCD equiv. ABN equiv. AEM equiv. AEFG.

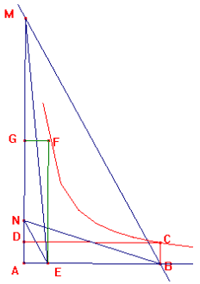
b) Al variare di E sulla semiretta AB, F descrive il ramo di iperbole equilatera avente per asintoti le semirette AB e AD, giacché indicata con k=area(ABCD) e detto AE=x, AG=y si ha xy=k, legge della proporzionalità inversa.

c) Riportati i segmenti OS=AB, OP=AD sulla semiretta Or e OR=AG e OQ=AE sulla semiretta Ot, osserviamo che i triangoli OPQ e ORS sono simili avendo l'angolo O in comune e i lati che lo comprendono in proporzione, giacché da AB*AD=AE*AG segue che OS*OP=OQ*OR e quindi OS:OQ=OR:OP. Ne consegue che gli angoli OQP e OSR sono congruenti, perché corrispondenti. 

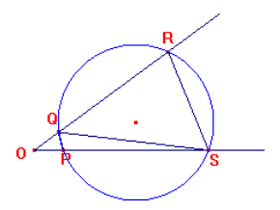
L'angolo PQR, essendo adiacente e quindi supplementare di OQP, lo sarà anche di PSR. Ne consegue che il quadrilatero PSRQ, avendo una coppia di angoli opposti supplementari, è inscrittibile in una circonferenza e pertanto i punti P, S, R, Q appartengono alla stessa circonferenza. Per costruire la circonferenza, basta tracciare gli assi di una coppia di lati del quadrilatero PSRQ.

Soluzione proposta da:
Classe 2^A - Scuola Media di Roveredo in Piano (PN) 

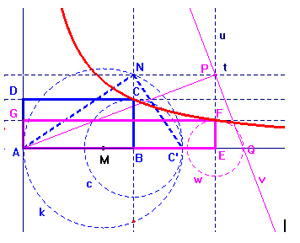
FIG. 1

a) (Fig.1)
Dato il rettangolo ABCD.

1. Circonferenza c di centro B, passante per C;
2. Intersezione di c con la semiretta AB alla destra di B: C';
3. Punto medio M tra A e C';
4. Circonferenza k di centro M, passante per A;
5. Intersezione di k con la retta BC: consideriamo N dalla parte di C rispetto alla retta AB.
   * In questo modo abbiamo determinato il triangolo AC'N, rettangolo in N (inscritto alla semicirconferenza di centro M e diametro AC') le cui proiezioni dei cateti sull'ipotenusa risultano congruenti alle dimensioni del rettangolo ABCD.
6. Retta t parallela alla semiretta AB, passante per N,
7. Punto E sulla semiretta AB;
8. Retta u perpendicolare alla semiretta AB; sua intersezione con t: P;
9. Segmento AP ;
10. Retta v, perpendicolare ad AP per P; sua intersezione con la semiretta AB: Q;
    * E è punto di animazione.
    Il triangolo rettangolo (per costruzione) APQ ha l'altezza rispetto all'ipotenusa, PE, congruente al segmento NB (altezza rispetto all'ipotenusa del triangolo AC'N). Il prodotto delle dimensioni delle proiezioni dei cateti sull'ipotenusa è uguale al quadrato della dimensione dell'altezza rispetto l'ipotenusa (Euclide); essendo l'altezza costante al variare di E, lo sarà anche il prodotto delle dimensioni dei segmenti AE ed EQ.
11. Circonferenza w di centro E, per Q; sua intersezione con u dalla parte di C: F;
12. Perpendicolare ad u per F e sua intersezione con la retta AD: G. Poligono (rettangolo) AEFG con i lati congruenti alle proiezioni dei cateti sull'ipotenusa (triangolo APQ).

b)
- Luogo di F al variare di E sulla semiretta AB: ramo di iperbole.
- Le grandezze rappresentate sono inversamente proporzionali.

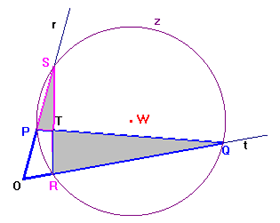
FIG. 2

c) (Fig.2)

(Costruzione: asse di due dei lati del quadrilatero PRQS; intersezione W; circonferenza z di centro W per S)
[La costruzione è solo una verifica, segue un tentativo di dimostrazione]

• Sappiamo che: il prodotto tra OP e OS è uguale al prodotto tra OR e OQ (per quanto detto al punto a)), da cui: il rapporto tra OP e OR equivale al rapporto tra OQ ed OS.
  Il rapporto precedente riferito alle dimensioni dei lati dei triangoli OPQ e ORS indica che essi sono simili, perché hanno l'angolo di vertice O in comune.
• Consideriamo i triangoli PST ed RQT (T è intersezione dei segmenti SR e PQ) che risultano simili avendo gli angoli corrispondenti congruenti (gli angoli di vertice T, opposti al vertice; gli angoli in S ed in Q sono congruenti per quanto detto al punto precedente). Il rapporto tra PT e ST equivale al rapporto tra RT e TQ.
• Si deduce l'uguaglianza tra i prodotti di ST, RT e PT, TQ.

Considerazioni:
Abbiamo trovato (aiutati dall'insegnante) nel manuale di Cabri, il teorema della potenza di un punto (Libro III degli elementi di Euclide, Proposizione 35), ci sembra però, che noi avremmo bisogno del suo inverso.

Quanta fatica!

[NOTA: dalla congruenza degli angoli PST e TQR si può dedurre (esiste un teorema apposito) che i punti S e Q appartengono ad un arco di circonferenza di estremi P ed R; lo stesso ragionamento si può fare a partire dai punti P ed R]

| Home Page Cabri | Torna a FLATlandia | Archivi |