 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Gennaio 2001
Il testo del problema:
a) E' dato un angolo XVY, di vertice V, minore di un
angolo piatto.
Considerato un punto I sulla sua bisettrice, I distinto da V, costruire le
circonferenze passanti per I e tangenti ai lati dell'angolo.
b) Che cosa rappresenta il punto I per i triangoli di vertice V formati dalle corde che congiungono i punti di contatto?
Giustificare le costruzioni e motivare le risposte.
Abbiamo ricevuto sei risposte, tre da ragazzi delle scuole
superiori e tre dalle scuole medie.
Le scuole che hanno partecipato sono:
Nel problema proposto si chiedeva la costruzione delle circonferenze tangenti ai lati di un angolo in un caso particolare, cioè passanti per un punto sulla bisettrice, e si chiedeva inoltre quale fosse il ruolo di quel punto rispetto a due particolari triangoli.
In una risposta non è stato interpretato correttamente il testo della prima parte. L'errore ha però avuto conseguenze interessanti, perché ha portato i ragazzi, con la guida dell'insegnante, alla scoperta, tramite il software Cabri, di due parabole luogo dei centri delle circonferenze passanti per il punto assegnato e tangenti ad un solo lato dell'angolo.
Nelle risposte accolte abbiamo individuato due modi per
ottenere la costruzione richiesta.
C'è chi ha fatto ricorso alla proprietà delle bisettrici, chi ha utilizzato la
proprietà dei segmenti di tangenza ad una circonferenza condotti da uno stesso
punto e chi ha fatto un miscuglio fra i due procedimenti. Non sempre il metodo
usato viene giustificato in modo esuriente.
Non tutti hanno interpretato secondo le aspettative la seconda parte. C'è chi
ha trovato che il punto assegnato e' equidistante dalle basi dei due triangoli
senza però motivare la risposta.
Pubblichiamo la prima parte della risposta inviata dalla Scuola Media di S. Genesio, simile a quella dell'IPSSAR "Artusi" e la soluzione completa proposta dalla classe 2E del L.S. "G.Galilei" di Bitonto (BA).
NOTA: Le correzioni o i commenti al testo sono riportate in parentesi quadra.
Soluzione proposta da:
Classe 3^ P - Scuola Media di S. Genesio (PV)
Se la circonferenza deve passare per I ed
essere tangente ai lati dell'angolo, la immaginiamo inscritta in un triangolo
avente per base la perpendicolare alla bisettrice e passante per I.
Costruiamo l'angolo XVY, poi la bisettrice dell'angolo, e prendiamo un punto I
su quest'ultima; tracciamo la retta perpendicolare alla bisettrice passante per
I.
Per trovare l'incentro del triangolo troviamo le intersezioni tra tale
perpendicolare e i lati dell'angolo, chiamandole M ed N.
Costruiamo la bisettrice dell'angolo VMN e troviamo l'intersezione tra le
bisettrici [punto O].
Questo punto è il centro di una circonferenza tangente ai lati dell'angolo [di
raggio OI].
La seconda circonferenza sarà inscritta in un quadrilatero avente come tre
lati, i lati dell'angolo e il segmento MN.
Perché un quadrilatero sia circoscrittibile ad una circonferenza le bisettrici
degli angoli [interni] devono passare per uno stesso punto.
Tracciamo la bisettrice dell'angolo MNX.
Facciamo l'intersezione tra le due bisettrici e chiamiamo il punto ottenuto K.
Tracciamo la circonferenza che è tangente ai lati dell'angolo il cui centro è
il punto K [di raggio KI].
Soluzione proposta da:
Classe 2E - Liceo scientifico "G. Galilei" Bitonto (BA)
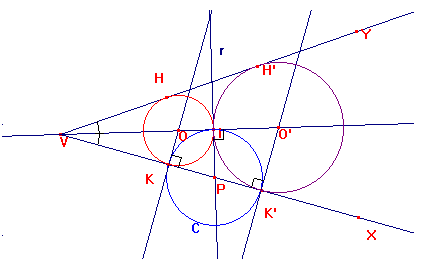
a) È dato un angolo XVY e un punto I appartenente alla sua bisettrice.
Si conduce la retta r perpendicolare alla bisettrice e passante per I.
Si costruisce la circonferenza C di centro P, punto di intersezione tra r e il
lato VX dell'angolo, e raggio il segmento PI.
Siano K e K' i punti intersezione fra C e VX e conduciamo per essi le rette
perpendicolari a VX. Siano O e O' i punti di intersezione tra dette
perpendicolari e la bisettrice.
Le circonferenze di centro O e raggio OK, di centro O' e raggio O'K', sono le
circonferenze richieste, poiché per costruzione passano per I e sono tangenti
ai lati dell'angolo dato.
Infatti OI=OK e O'I=O'K' perché segmenti di tangenza condotti da punti esterni
a C ed inoltre essendo la bisettrice asse di simmetria per l'angolo, lo è anche
per le circonferenze costruite e questo garantisce la tangenza al lato VY nei
punti H e H' simmetrici di K e K' rispetto alla bisettrice.
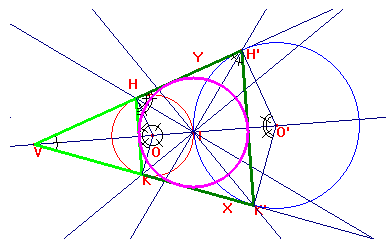
b) Si traccino le corde HK e H'K'. Il punto I
risulta essere l'ex-incentro del triangolo VKH, rispetto al lato HK, perché
punto di incontro della bisettrice dell'angolo in V e di quella dell'angolo
esterno KHY : infatti gli angoli IHY e IHK risultano congruenti perché angoli
alla circonferenza a cui corrispondono angoli al centro congruenti(HOI=IOK
perché supplementari di angoli congruenti per il teorema delle tangenti
condotte da un punto esterno).
Per il triangolo VK'H', I risulta essere l'incentro, perché punto di incontro
delle bisettrici dei suoi angoli interni, H'VK' e VH'K': infatti VH'I=IH'K'
perché corrispondono angoli al centro congruenti (H'O'I=IO'K') per il teorema
citato precedentemente.
| Home Page Cabri | Torna a FLATlandia | Archivi |