 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Febbraio 2001
Il testo del problema (quasi un gioco):
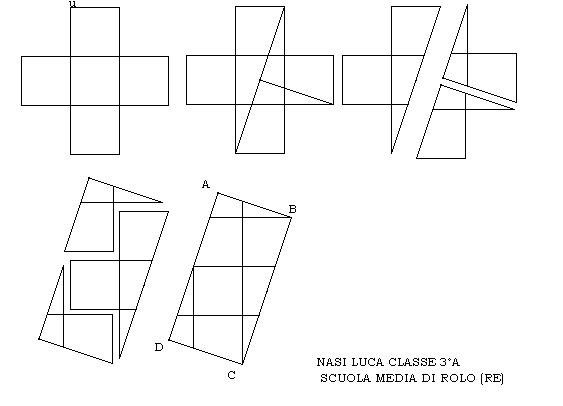
Disegnate un quadrato di lato 1 (uno) rispetto ad una unità di misura u
e, su ciascun lato, esternamente, disegnate ancora un quadrato di lato 1u.
Si ottiene una croce formata da cinque quadrati che dovrete ritagliare
lungo il suo perimetro.
Avete ora a disposizione due tagli da effettuare sulla croce (passando
per il centro della figura iniziale): col primo si divide la figura in due
parti, col secondo una sola di queste viene divisa ancora in due parti.
I tre pezzi così ottenuti dovranno essere tali che, ricomposti come in un
puzzle, formino un rettangolo, equivalente alla croce, con una dimensione
doppia dell'altra.
Giustificare la costruzione del rettangolo e calcolare la lunghezza dei suoi lati rispetto alla unità u.
Commento
Il problema di Febbraio era stimolante ma insidioso, come dice giustamente Daniele Urzì, un ragazzo appassionato di questioni geometriche, che ci invia le sue soluzioni anche se “fuori gara” per superati limiti di età. Commenta così la sua soluzione:
…Il problema era effettivamente “quasi un gioco”. Ma appunto, “quasi”, perché, una volta trovata la soluzione, che da un punto di vista intuitivo è semplice, viene il compito gravoso di giustificarla.
Essendoci nella figura tante proprietà “evidenti” bisogna fare bene attenzione, perché il rischio, in questi casi, è di fare delle affermazioni senza però le dovute giustificazioni…
Oltre a quella prima citata, abbiamo
ricevuto diciassette risposte di cui cinque provengono da scuole medie
inferiori.
Il problema proponeva di tagliare una croce formata da cinque quadrati per
trasformarla in un rettangolo equivalente e formato da due quadrati.
In una sola risposta non è stato individuato il taglio corretto: probabilmente
il solutore non ha controllato con carta e forbici la sua congettura o non ha
interpretato correttamente la richiesta.
In tutte le altre risposte sono state individuate correttamente, in modo
intuitivo o in seguito al calcolo algebrico, le linee secondo cui tagliare la
figura, ma, nella maggior parte di esse, la costruzione del rettangolo richiesto
è stata basata sulla evidenza e scarsamente o incompletamente giustificata.
Questo può essere accettato, come più volte detto, per le scuole medie
inferiori, ma non per i ragazzi delle superiori ai quali si chiede di avvalorare
le loro intuizioni in modo consapevole.
Siamo dispiaciuti per i ragazzi che si sono cimentati nel problema e che non
troveranno pubblicati i loro lavori. Come alle Olimpiadi, l’importante è
partecipare.
Vediamo brevemente le fasi della dimostrazione:
Le diagonali secondo cui eseguire i tagli devono essere uguali, perpendicolari e dividersi in due parti congruenti. La dimostrazione più interessante di questo punto è stata effettuata in una delle due risposte dell’istituto “Michelangelo”.
Le diagonali suddette dividono la croce in quattro poligoni congruenti. Questo fatto è stato parzialmente evidenziato, ma non giustificato, nelle risposte dell’ITG “Rondani” e del LS “Galilei” di Adria.
Una volta ricomposta la figura (sovrapponendo, traslando o ruotando) si deve verificare che si ottiene un quadrilatero dimostrando che le due semidiagonali che si ricongiungono si dispongono su una stessa retta. Questo si intuisce implicitamente nella risposta del LS “Galilei” di Bitonto e viene superato, inconsapevolmente, sia nella seconda parte della risposta della Scuola Media di Rufina, sia in quella dell’ITG “Rondani”
Il problema dell’allineamento, se non è esplicitamente posto, spesso sfugge ai ragazzi quindi, come già detto nello scorso anno, ci sembra utile proporlo almeno in uno dei problemi dell’anno.
Dobbiamo inoltre far notare che chi ricorre ai movimenti nel piano è tenuto a precisare il verso (oltre il centro e l’angolo) nelle rotazioni e, nelle traslazioni, secondo quale vettore.
Le scuole che hanno partecipato sono:
Scuola Media di San Genesio (PV)
Scuola Media di Rolo (RE)
SM "Graziosi" di Savignano s.P. (MO)
Scuola Media di Rufina (FI)
Scuola Media di Roveredo in Piano (PN)
LG "ISISS" di Oderzo (TV)
LS "B. Russell" di Roma (RM)
LS "G.Galilei" Bitonto (BA)
LS "G. Galilei" di Adria (RO)
LS "E. Amaldi" di Bitetto (BA)
ITCG "E. Majorana" di Castrolibero (CS)
LS "F. D'Assisi" di Roma (RM)
ITI "Fermi" di Mantova (MN)
ITI, LST "Berenini" di Fidenza (PR)
LS "Michelangelo" di Forte dei Marmi (LU), (due risposte)
ITC "C. Rondani" Parma (PR)
Abbiamo stabilito di riportare in questa pagina:
per le scuole medie inferiori:
le figure della scuola di Rolo a corredo del testo del problema.
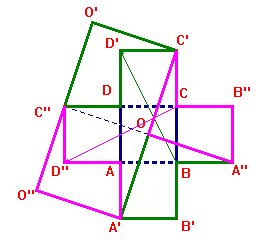
la figura con animazione della scuola di Roveredo, seguita dalla risposta di S. Genesio
la conclusione, con figura, della costruzione della scuola di Rufina
per le scuole superiori:
la risposta del LS “G. Galilei” di Bitonto
la prima parte della risposta del LS “Michelangelo
la parte conclusiva della costruzione inviata dall’ITG “Rondani”, essendo la prima parte incompleta sia nelle descrizioni sia nelle giustificazioni.
NOTA: Le correzioni o i commenti al testo sono riportate in parentesi quadra.
SOLUZIONI
Scuola Media di Roveredo in Piano. (PN)
SELEZIONARE
QUI PER VEDERE
LA FIGURA ANIMATA CABRIJAVA
Scuola media di S.
Genesio (PV)
Classe 3 P
Siamo
la classe 3°P della scuola media di S.Genesio (Pavia), e vi inviamo la nostra
risoluzione al problema, pubblicato su FLATlandia, del mese di febbraio.
Discutendo in classe abbiamo capito che la misura dei lati del rettangolo non
poteva essere un numero intero perchè 1*2=2unità quadrate oppure 2*4=8 u.q.
e
quindi abbiamo cercato altri segmenti.
Il
primo tentativo è stato quello di tracciare la [una] diagonale del rettangolo
formato da 3 quadrati e con Pitagora [applicando il teorema di …] abbiamo
calcolato la sua misura.
Abbiamo trovato radice quadrata di 10, allora l'altra dimensione doveva essere
la metà: radice quadrata di 10 diviso 2 e il prodotto viene 5unità quadrate.
Così abbiamo capito che eravamo sulla strada giusta e il primo taglio l'abbiamo
fatto lungo la diagonale e il secondo con qualche tentativo abbiamo cercato un
segmento lungo come metà diagonale [e perpendicolare alla precedente].
A questo punto abbiamo unito i tre pezzi così ottenuti e abbiamo trovato il rettangolo equiesteso alla figura di partenza.
[…]
Scuola
Media di Rufina (FI)
Classe 3C
Il gruppo di alunne (Pazzi M. e Aimavilli I. in primo luogo) hanno messo mano alla prima parte dell'attività, nella quale c'è stato effettivamente anche il ritaglio e la manipolazione della figura. Successivamente con Cabrì alcuni altri, Bavecchi, Santoni e Capecchi, hanno reso un "doppione" di quel che era stato fatto con la carta. [tratto dal commento dell'insegnante]
[…]
Alunno Bavecchi Massimiliano
Costruzione del rettangolo:
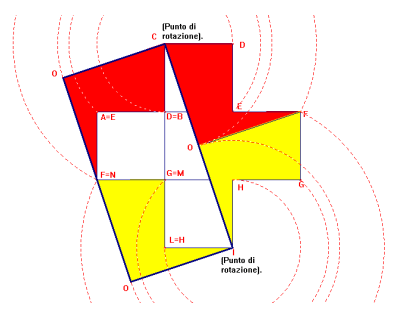
Facendo
ruotare di 90° la figura COFED, intorno al punto F in senso orario, si formerà
un quadrato OFCI di lato congruente a metà diagonale (OI=OF).
Quindi facendo ruotare le 2 figure COFED e OIHGF, che compongono tale
quadrato rispettivamente di 270 ° [rispettivamente] intorno al punto C, in
senso antiorario e intorno al punto I, in senso orario , si andranno a formare
due quadrati di lato CO e OI , ciascuno congruente al quadrato OFCI. Uniti
formeranno un rettangolo di base CI, diagonale del rettangolo CDIL e di altezza
ON congruente a OF ossia metà diagonale del rettangolo CDIL.
Così si è formato un rettangolo di base doppia dell’altezza.
LS "G. Galilei"
- Bitonto (BA)
Classe 2E
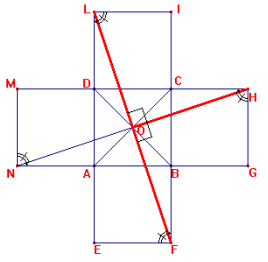
Per ottenere dalla croce di area 5u2, con due tagli che passino dal centro O del quadrato ABCD di partenza, tre parti tali che, come un puzzle, formino un rettangolo equiesteso e avente una dimensione doppia dell'altra abbiamo fatto il seguente ragionamento:
1) Imponendo che l'altezza del
rettangolo misuri x, la base 2x e l’area 5, abbiamo l'equazione: 2x2=5,
da cui x=(sqr(10))/2.
Pertanto i lati del rettangolo da ottenere sono sqr(10) e (sqr(10))/2.
2) Il triangolo LEF, rettangolo per
ipotesi in E, ha LE=3u, EF=1u e quindi LF=sqr(10),
applicando il teorema di Pitagora.
Dunque il primo taglio da effettuare sarà lungo il segmento LF che costituirà
la base del rettangolo.
3) Gli assi mediani del quadrato di partenza ABCD (retta per O parallela ad AD e retta per O parallela ad AB) sono per costruzione anche assi di simmetria della croce e dei rettangoli EFIL e NGHM, pertanto O è anche centro di simmetria di queste figure (ogni figura dotata di due assi di simmetria perpendicolari è dotata di centro di simmetria, punto di incontro dei due assi). Pertanto le diagonali LF e NH sono congruenti (diagonali di rettangoli congruenti) e si tagliano scambievolmente a metà in O.
4) Gli angoli in cui tali diagonali dividono gli angoli retti in H,L,N,F sono a due a due congruenti, perché alterni interni di rette parallele per costruzione, e complementari.
5) Le diagonali LF e NH sono inoltre perpendicolari in O, poiché nel triangolo OTF , dove T è il punto intersezione di OH con CB, i due angoli acuti OTF e OFT sono complementari (OTF=OHG [perché] corrispondenti di [rispetto ai segmenti] HG e CB paralleli, tagliati da NH)

6) Operati i tagli e ricomposti secondo la figura 2, ci rendiamo conto che [NON BASTA! Occorre giustificare che] i due pezzi verde e fucsia completano perfettamente il poligono azzurro dando luogo al rettangolo richiesto, grazie alle ampiezze degli angoli sopra considerati [PERCHE' …].
Alessandro Navari,
LS "Michelangelo" - Forte dei Marmi (LU)
Classe 2C PNI
Dopo la costruzione del quadrato dato il
lato, e dei quadrati su ogni dei lati del quadrato di partenza ho
proceduto al taglio della croce.
Con il primo taglio dovevamo dividere in due parti uguali la figura e la ho
tagliata seguendo la diagonale NF.
Con il secondo taglio ho diviso in due parti uguali una delle due figure
risultanti dal primo taglio.
Per giustificare la costruzione finale del rettangolo e dire che un lato è
doppio dell’altro ho effettuato la seguente dimostrazione.
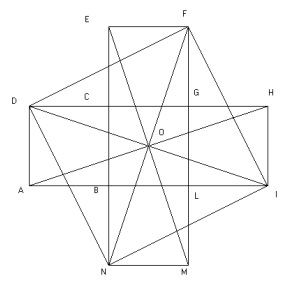
Per prima cosa ho dimostrato che tutte le diagonali dei rettangoli NMEF e ADIH sono uguali per i seguenti motivi: se consideriamo i triangoli NMF, NEF, DIH, AHI sono tutti uguali per il primo criterio poiché hanno i cateti minori uguali che sono i lati dei quadrati, i cateti maggiori uguali per somma di segmenti uguali (lati dei quadrati), e l’angolo retto compreso fra essi [questa dimostrazione è superflua].
Dopo questo ho tracciato i segmenti DF,
FI, IN, ND e dimostrato che sono uguali e che sono i lati del quadrato che ha
come diagonali DI, FN.
Se considero i triangoli DGF, FLI, IBN, DCN dico che sono uguali per il primo
criterio perché hanno come cateti minori i lati dei quadrati, come cateti
maggiori la somma di [due] segmenti uguali (lati dei quadrati) e l’angolo
retto compreso tra loro, quindi i lati tracciati prima sono uguali.
Per dimostrare che questi lati formano
un quadrato sfrutto gli angoli dei triangoli precedenti.
Per un noto teorema sappiamo che a cateto minore corrisponde angolo minore e
viceversa a cateto maggiore corrisponde angolo maggiore. La somma degli angoli
interni dei triangoli è 180°.
Gli angoli dei nostri triangoli li chiamiamo X, Y, Z. Z è l’angolo opposto
all’ipotenusa (90°), X l’angolo opposto al cateto maggiore e Y è
l’angolo opposto al cateto minore.
Tutti i triangoli sono rettangoli ed essendo Z retto, allora X+Y=90°.
Essendo l’angolo DFI formato
dall’angolo X e dall’angolo Y, è di [misura] 90° come [e nello stesso modo
si dimostra che] sono retti tutti gli angoli della figura [DFIN].
Adesso ho dimostrato che è un quadrato e so che le diagonali del quadrato sono
bisettrici e che si dimezzano scambievolmente [e sono fra loro perpendicolari].
[…]
Rizzardi Pier
Alessio, ITG "Rondani" (PR)
Classe 2I
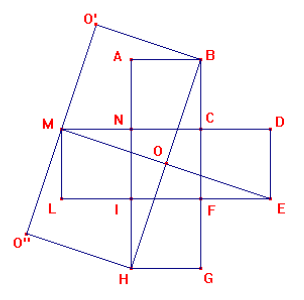
[…]
Il lato OE è uguale al lato OH perché metà di lati uguali. Quindi la figura OHGFE incastrandosi con la figura OMLIH, congruente alla prima per dimostrazione precedente, darà origine a un quadrato MOHO’’. Facendo lo stesso con la figura OEDCB si nota la comparsa di un rettangolo che ha le dimensioni una doppia dell’altra, essendo BOMO’’ congruente a OHO’’M
| Home Page Cabri | Torna a FLATlandia | Archivi |