Soluzioni Dicembre 2000

FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Data una circonferenza k di diametro AB tracciare una corda AC e prolungarla di un segmento CD congruente a CB.

a) Dimostrare che, dovunque sia C, l'asse del segmento BD passa per il punto medio della semicirconferenza di diametro AB e contenente C.

b) Qual è il luogo descritto dal punto D al variare di C su k? Giustificare la risposta.

Abbiamo ricevuto cinque risposte provenienti da cinque scuole di cui due scuole medie inferiori.
Le scuole che hanno partecipato sono:

Nel problema proposto si trattava di dimostrare prima una proprietà invariante della figura assegnata e di individuare poi il luogo descritto dall'estremo di un segmento, ottenuto prolungando una corda di circonferenza, al variare dell'altro estremo sulla circonferenza. In tutte le risposte pervenute sono state svolte le due parti del problema, ma non sempre in modo corretto e completo, soprattutto nella seconda parte. Una risposta non è stata accettata in quanto presentava un errore nel metodo della dimostrazione nella prima parte e una errata interpretazione del luogo. Si rendono necessarie alcune osservazioni:

Fra le soluzioni accolte abbiamo scelto di presentarne una della scuola superiore (LS "G. Galilei" di Bitonto) e una di scuola media inferiore (SM di Roveredo in Piano): anche se incomplete nella seconda parte, esse sono esaurienti nella prima e corrette nella esposizione.

Soluzione proposta da:
Classe 3^ A - Scuola Media Statale di Roveredo in Piano (PN)

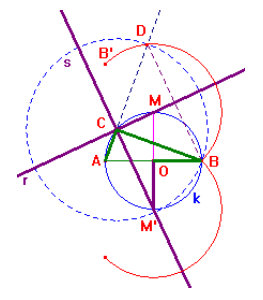(Semiretta AC con C sulla circonferenza k di centro O, circonferenza di centro C per B e sua intersezione con la semiretta AC: D; asse r del segmento BD)

a)
1. Tracciando il segmento CB si ottiene l'angolo retto ACB (C sta sulla circonferenza e i lati passano per gli estremi del diametro);
2. L'asse r del segmento BD è bisettrice dell'angolo retto DCB (retto, perché adiacente dell'angolo ACB retto);
3. Tracciamo la bisettrice s dell'angolo retto ACB; le rette r ed s risultano tra loro perpendicolari perché bisettrici di angoli adiacenti;
4. Sappiamo che se un angolo alla circonferenza è retto le intersezioni dei lati con la circonferenza individuano un diametro, quindi M ed M' (intersezioni di r ed s con k) determinano un diametro di k, che risulta perpendicolare ad AB (all'angolo alla circonferenza M'CB di 45° corrisponde un angolo al centro M'OB di 90°).
Quindi ogni punto estremo dei due diametri è punto medio della semicirconferenza, su cui sta, individuata dall'altro diametro.
b)
[Il luogo è descritto, ma non pienamente giustificato]
Luogo: la semicirconferenza (alla destra della perpendicolare al diametro AB, passante per A) di centro M e diametro BB' (B' è il simmetrico di B rispetto ad M) e la sua simmetrica rispetto al diametro AB.
Il segmento BD è una corda della circonferenza di centro M e si fa diametro quando contiene il centro. L'asse r, durante il movimento di C
sull'arco BMA da B ad A, compie una rotazione di 90° di centro M, ed essendo bisettrice dell'angolo BCD, provoca una rotazione doppia [cioè di 180°] di D e lo porta da B a B'.
Se C si muove nell'arco AM'B da A verso B il punto D completa il luogo e le considerazioni sono analoghe alle precedenti.

Soluzione proposta da:
Classe 2 E - Liceo scientifico "G. Galilei" Bitonto (BA)

a)
Disegnata la circonferenza k di diametro AB, tracciata la corda AC, con C più vicino ad A che a B (vedi fig.1) e prolungata di un segmento CD=CB si fanno le seguenti considerazioni:
1) Il triangolo ACB è rettangolo in C essendo inscritto in una semicirconferenza,
2) il triangolo DCB per costruzione è rettangolo in C e isoscele, per cui l'angolo CBD misura 45°,
3) r, asse di DB, passa da C, divide l'angolo DCB in parti congruenti essendo anche bisettrice nel triangolo isoscele CBD,
4) se M è l'ulteriore punto di intersezione di r con la circonferenza k, si ha che BCM=BCN=45° ed in quanto angolo alla circonferenza insiste sull'arco BM=1/4 di k (un arco che e' visto da un punto della circonferenza sotto un angolo di 45° è sempre un quarto della circonferenza),
5) ne consegue che M è punto medio della semicirconferenza ACM.
Nel caso in cui C è proprio il punto medio dell'arco AB, la tesi è ovvia conseguenza del punto 3). In questo caso particolare si può osservare che r risulta tangente in C a k in quanto l'angolo OCN diventa retto, conseguenza del fatto che OBNC è un quadrato. Se C è più vicino a B (vedi fig 2), l'osservazione 4) va così modificata:
4 bis) l'angolo alla circonferenza ACM=45° perchè opposto al vertice di BCN=45° e quindi l'arco AM=1/4 di k.
Analoghi discorsi se C appartiene all'altra semicirconferenza di diametro AB.


Fig. 1	Fig. 2

b)
Poiché M appartiene all'asse di BD per dimostrazione precedente ne consegue che MD=MB con MB=MA essendo queste ultime corde che insistono su archi congruenti, quindi MA=MB=MD.
Questo vale qualunque sia la posizione di C su k.
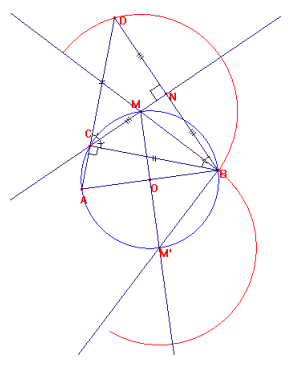
Il luogo descritto da D sono la semicirconferenza di centro M e raggio MB e la semicirconferenza di centro M' e raggio M'B, dove M' è il punto medio dell'altra semicirconferenza (fig. 3). [. . .]
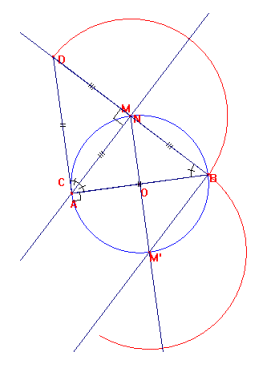
[In fig. 4 il caso C=A]


Fig. 3	Fig. 4