FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Aprile 2001

Il testo del problema:

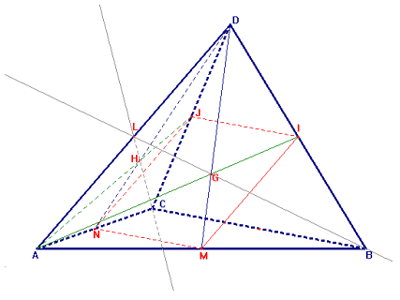
E' data una piramide a base triangolare (cioè un tetraedro) di vertici A, B, C, D.
Consideriamo i punti medi M e N rispettivamente degli spigoli AB e AC e li congiungiamo con il vertice D.
Consideriamo inoltre i punti medi I e J rispettivamente degli spigoli BD e CD e li congiungiamo con il vertice A.
Indichiamo con G l'intersezione di MD con AI e con H l'intersezione di ND con AJ.
Tracciamo i segmenti MN, IJ, GH.

  1. Dove si incontrano le rette BG e CH?
  2. Di che natura è il quadrilatero MNIJ?
  3. Qual è il rapporto fra i segmenti GH e MN?
  4. Qual è il rapporto fra i volumi delle due parti in cui il tetraedro viene diviso dal piano AIJ?

Giustificare le risposte.

Commento

Abbiamo ricevuto cinque risposte, una sola delle quali proviene da una scuola media.
Il problema di questo mese riproponeva le proprietà dei punti medi e delle mediane di un triangolo applicate però ad una figura tridimensionale: un tetraedro.
Ricordiamo che il tetraedro non è necessariamente un poliedro regolare né una piramide retta, nel testo si parla infatti di piramide triangolare senza altri attributi. Una delle risposte pervenute non è quindi accettabile perché in essa si considera esclusivamente un tetraedro regolare.
Anche noi però abbiamo commesso un errore: nel punto 2) del testo abbiamo chiesto qual è la natura del quadrilatero MNIJ pensandolo come parallelogramma; in realtà il parallelogramma è MNJI.
Solo i ragazzi della scuola media hanno quindi risposto correttamente dicendo che quel quadrilatero è intrecciato (anche se hanno tratto le loro deduzioni nel caso particolare del tetraedro regolare). I ragazzi delle superiori invece, anche se hanno interpretato la nostra intenzione, sono caduti nel nostro stesso errore non segnalando lo scambio di lettere.
Abbiamo convenuto di presentare, con le dovute osservazioni, entrambi i tipi di risposta.

Le scuole che hanno partecipato sono:

Nessuna delle soluzioni accolte è integralmente corretta, per cui riporteremo per qualche risposta prescelta le parti più significative:

Ricordiamo che alle soluzioni inviate dalle scuole medie non richiediamo che siano sempre esaurienti nelle giustificazioni, ma che siano perlomeno complete nella esposizione.

NOTA: Le correzioni al testo o i commenti sono scritti in parentesi quadra.
Sono racchiuse in doppia parentesi quadra le parti ritenute superflue.

Soluzione proposta da:
Classe 3P - Scuola Media di San Genesio (Pavia)

Dopo alcuni tentativi per capire quali fossero le relazioni tra i vari enti geometrici fatti col disegno e con Cabri, per trovare la soluzione del problema la prof. ci ha portato in classe cannucce e scovolini per pipa, ago e filo per unire i vertici con i punti medi, e così la costruzione ci è apparsa subito molto chiara.
Abbiamo costruito un tetraedro regolare, ma rileggendo bene il testo abbiamo dedotto che il tetraedro poteva non essere necessariamente regolare. Le osservazioni che abbiamo fatto valgono comunque anche per un tetraedro non regolare, poiché si basano su proprietà delle mediane vere per un triangolo qualsiasi.

1) I segmenti DM, DN, AI e AJ sono mediane, in quanto congiungenti i vertici D e A con i rispettivi punti medi dei lati opposti. Quindi i punti G e H sono rispettivamente baricentro dei triangoli ABD e ACD.
Le rette BG e CH, passando rispettivamente per i baricentri G e H tagliano il lato AD, spigolo in comune alle facce ABD e ACD, nel suo punto medio.

2) Nel tetraedro regolare il quadrilatero MNIJ è un quadrilatero intrecciato con i lati MN e IJ di uguale lunghezza perchè congiungenti punti medi di due triangoli equilateri uguali, e paralleli perchè i triangoli DBC e ABC si corrispondono in una rotazione attorno all'asse BC di 60°.
[[I segmenti MJ e IN sono uguali e perpendicolari perchè diagonali del quadrato MNJI (MI=NJ perchè congiungenti punti medi di triangoli equilateri uguali) [parte incompleta e superflua]]].
Abbiamo controllato con Cabrì che anche nel tetraedro non regolare si mantengono sia il parallelismo, sia l'uguaglianza dei lati MN e IJ [questa affermazione poteva essere facilmente giustificata].
[...]

Soluzione proposta da:
Politi Stefano e Langella Emiliano - L.S. "F. d'Assisi" Roma

1) Se prendiamo in considerazione il triangolo ADB e le mediane DM e AI risulta che il punto G è il baricentro. Quindi la retta passante per il vertice B e per il baricentro incontrerà DA nel suo punto medio.

Se prendiamo in considerazione il triangolo ADC e le mediane AJ e DI [DN] risulta che il punto H è il baricentro. Quindi la retta passante per il vertice B[C] e per il baricentro incontrerà DA nel suo punto medio.
Quindi BG e CH si incontrano nel punto medio del lato DA.

2) Se consideriamo il triangolo ACB, il segmento NM è la congiungente dei punti medi dei lati AC e AB, quindi è la parallela a CB e congruente alla sua metà.

Se consideriamo il triangolo DCB, il segmento IJ è la congiungente dei punti medi dei lati DC e DB, quindi è la parallela a CB e congruente alla sua metà.
Quindi MN è parallela e congruente a JI, quindi il quadrilatero JINM [come evidenziato nel commento era corretto scrivere IJNM] è un parallelogramma.

3) Se consideriamo DG osserviamo che è il doppio di GM perché la parte di mediana che va dal vertice al baricentro è doppia di quella che va dal baricentro al punto medio del lato.
Quindi il segmento DG è 2/3 della mediana GM[DM].

Per lo stesso discorso fatto sulla mediana DN risulta che DH è 2/3 di DN.
I triangoli DHG e DNM sono simili perché hanno un angolo in comune e 2 lati in proporzione e il rapporto che lega i lati è 2/3. Da questo deduciamo che HG è 2/3 di MN.

Soluzione proposta da:
Classe 2E - L.S. "G. Galilei" Bitonto (BA)

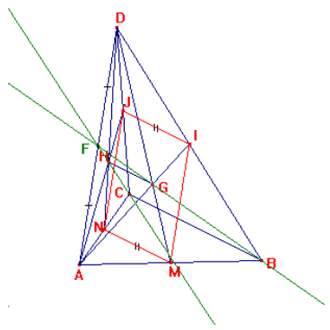
1) Costruita la piramide triangolare ABCD e presi in considerazione i punti medi indicati nella traccia, si ha che G, essendo il punto intersezione di MD con AI, entrambe per costruzione mediane nella faccia ABD, ne è il baricentro e quindi appartiene alla faccia; analogamente H è il baricentro e appartiene alla faccia ACD, in quanto punto di incontro di sue mediane: ND e AJ.
La retta BG, pertanto, conterrà la terza mediana di ABD e quindi intersecherà AD nel suo punto medio F (le tre mediane di un triangolo si intersecano nel baricentro), così come la retta CH conterrà la terza mediana di ACD e intersecherà ancora AD nel punto medio F. Quindi le rette BG e CH si incontrano nel punto medio dello spigolo AD .

2) Nel triangolo di base ACB, MN è il segmento congiungente i punti medi di due lati per cui è parallelo al terzo lato BC ed è congruente alla sua metà. Analogamente nel triangolo DCB, faccia laterale della piramide, JI è il segmento congiungente i punti medi di due lati e quindi è ancora parallelo al terzo lato BC e congruente alla sua metà. Ne consegue che MN=IJ e MN // JI per transitività e dunque il quadrilatero MNIJ [come evidenziato nel commento era corretto scrivere MNJI] è un parallelogramma, avendo due lati opposti paralleli e congruenti.

3) Il baricentro di un triangolo divide ogni mediana in due parti di cui quella che contiene il vertice è doppia dell'altra, pertanto DG=2GM e DH=2HN. Nel triangolo sezione DMN, il segmento HG individua sui lati DN e DM segmenti proporzionali e pertanto è parallelo al terzo lato NM. Ne consegue che il triangolo DHG risulta simile ad DNM e il rapporto di similitudine è dato da DH/DN=2/3, da cui anche HG/NM=2/3.

4) Il piano AIJ divide il tetraedro in due piramidi: ABCIJ di base il trapezio CBIJ e la piramide AIJD di base il triangolo DIJ. Si osserva che le due piramidi ottenute hanno la stessa altezza, data dalla distanza del vertice comune A dal piano di base comune DCB, poiché le basi sono le parti in cui la faccia DCB resta divisa dal segmento IJ parallelo al lato BC. Pertanto il rapporto fra i volumi delle due piramidi è uguale a quello delle aree delle basi, tenendo conto della formula V=Ab*h/3.
Considerando che IJ è il segmento congiungente i punti medi di due lati di DCB, esso stacca il triangolo DIJ che è simile a DCB [con] rapporto [di similitudine] ½ e pertanto Area(DIJ)=(1/4)*Area(DA[C]B), da cui Area (BCJI)=(3/4)*Area(DA[C]B) e infine Area(DIJ)=3[(1/3)]*Area(BCIJ). Per quanto detto in precedenza allora anche il rapporto fra i volumi delle due piramidi [nell'ordine citato all'inizio] è 3.

| Home Page Cabri | Torna a FLATlandia | Archivi |