 FLATlandia
FLATlandia FLATlandia
FLATlandia
Ottobre 1999
Il testo del problema:
Dato un quadrato, costruire un rettangolo in esso inscritto con i lati
paralleli alle diagonali del quadrato.
Consideriamo ora la famiglia dei rettangoli aventi le caratteristiche
richieste:
a) qual è la relazione fra i loro perimetri?;
b) qual è il rettangolo di area massima? Qual è il rapporto fra la sua
area e quella del quadrato assegnato?
Motivare le risposte
Premessa:
Il problema proponeva innanzi tutto di determinare una costruzione che, anche
se semplice, doveva essere descritta. Seguivano poi due quesiti e il calcolo di
un rapporto.
Pochi hanno descritto la costruzione e non tutti hanno motivato le risposte ai
quesiti. Le soluzioni inviate dagli allievi di scuola elementare e di scuole
medie, anche se carenti nelle giustificazioni, testimoniano comunque un lodevole
impegno.
Fra le risposte giunte dalle scuole superiori alcune non sono accettabili per la
completa mancanza di giustificazioni (una di esse inoltre esamina solo casi
particolari).
Anche fra le soluzioni considerate "accettabili" si riscontrano
comunque imprecisioni e carenze di vario tipo.
Si rendono necessarie alcune osservazioni:
Le scuole che hanno partecipato sono:
Per il mese di ottobre sono state accettate le soluzioni delle seguenti scuole:
NOTA: Come consuetudine nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre.
SOLUZIONE
AL PROBLEMA DI OTTOBRE PROPOSTA DALLA CLASSE 2 B
Liceo
Sc. “Francesco d’Assisi” ROMA
SECONDA PARTE DELLA SOLUZIONE INVIATA DA:
IPSSAR "P.Artusi" di Forlimpopoli;

SOLUZIONE INVIATA DA:
Classi II-A Scuola Media di Roveredo di Piano (PN).
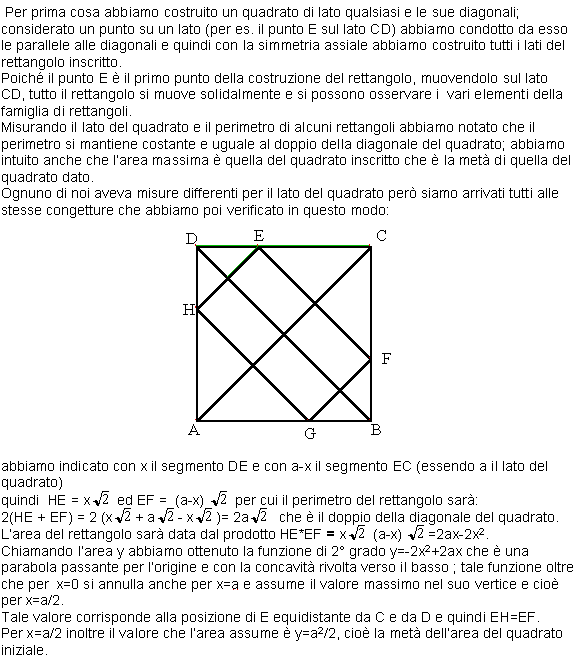
COSTRUZIONE:
disponibili 2 animazioni CabriJava (vedi sotto)
1. circonferenza c di centro O;
2. retta r passante per O;
3. retta s perpendicolare ad r e passante per O;
4. intersezioni della circonferenza c con le rette r ed s (E, F, G, H);
5. poligono (quadrato) EFGH;
6. punto A sul lato EF (sovrapposto segmento EF per esigenze di animazione);
7. parallela t alla retta s [passante per A];
8. retta u simmetrica di t rispetto la retta s;
9. intersezioni delle rette u e t con il quadrato EFGH;
10. poligono (rettangolo) ABCD;
11. punto medio M del segmento EF;
PUNTO DI ANIMAZIONE IN A SUL SEGM. EF.
RISPOSTE:
a) I rettangoli che si ottengono animando [o TRASCINANDO: l'animazione e'
presente solo in Cabri II] A sul segmento EF sono ISOPERIMETRICI.
b) Il rettangolo di area massima si ottiene quando A coincide con M, cioè
quando il rettangolo si fa quadrato.
2. L'area del quadrato EFGH è doppia dell'area del quadrato ABCD.
SOLUZIONE INVIATA DA:
Classi III-A Scuola Media di Roveredo di Piano (PN).
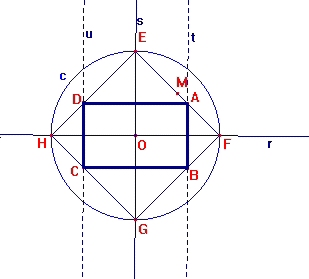
COSTRUZIONE PER OTTENERE RETTANGOLI ISOPERIMETRICI:
disponibili 2 animazioni CabriJava (vedi sotto)
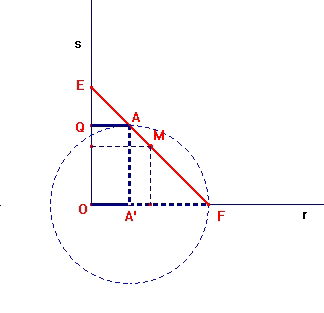
1. due semirette (r, s) perpendicolari con la stessa origine in O;
2. segmento OF [su r];
3. segmenti OA' ed A'F [su r];
4. parallela ad s passante per A';
5. circonferenza con centro in A' passante per A'F,
6. punto A (intersezione della circonferenza con la parallela ad s [passante
per...]); [ segmenti A'A ed AQ (utilizzando una perpendicolare ad s)]
PUNTO DI ANIMAZIONE A' SUL SEGM. OF.
7. luogo del punto A animando A' (EF);
8. segmento EF e suo punto medio M. I rettangoli (OQAA') che si generano sono
isoperimetrici essendo la somma dei lati , OA', AA' costante (=OF);
b)
1. L'area massima la si ottiene quando il rettangolo si fa quadrato (A coincide con il punto medio del segmento EF).
2. Quando A si trova in M il poligono OQAA' è quadrato ed i triangoli
rettangoli (per costruzione) AA'F ed EQA sono isosceli con i cateti congruenti
ai lati del quadrato.
La somma delle aree dei due triangoli equivale all'area del quadrato, quindi:
Area OEF = 2 Area OQAA'.
Il ragionamento si trasferisce sulla prima costruzione (della 2A):
L'area del quadrato EFGH è doppia dell'area del quadrato ABCD
(A coincide con M).
SOLUZIONE INVIATA DA:
Seconde classi liceo scientifico "G. Galilei" Bitonto
Parte a)
Costruito [manca la descrizione] il quadrato ABCD e il rettangolo PQRS [con P su AB] in esso inscritto con i lati paralleli alle diagonali (vedi Galilei Bitonto parte a ottobre 99.fig allegata), si ha che:
PBU [i punti U,V,Z,T sono rispettivamente le intersezioni dei lati del
rettangolo con le diagonali del quadrato] è un triangolo rettangolo isoscele,
poiché in un quadrato le diagonali sono bisettrici degli angoli e sono
perpendicolari fra loro e quindi PUB = 90° e PU = BU.
Analogamente APT è rettangolo isoscele e quindi PT = AT.
In un quadrato le diagonali sono assi di simmetria, pertanto anche BU = PU = QU
= SZ = RZ, AT = PT = ST = QV = VR. Da ciò segue che il perimetro del rettangolo
è congruente alla somma delle diagonali del quadrato, qualunquesia il
rettangolo al variare di P su AB. Vale a dire che tutti i rettangoliinscritti
sono isoperimetrici.
Parte b)
Nel quadrato ABCD viene inscritto ulteriormente il quadrato EFGH ( vedi
Galilei bitonto parte b.fig) [con E su AB] . Il quadrato EFGH ha area maggiore
di un qualsiasi rettangolo PQRS, infatti:
il rettangolo ILMN [i punti I, L, M, N sono rispettivamente le intersezioni dei
lati del rettangolo con i lati del quadrato inscritto] è in comune ed EILF >
LQRM, avendo altezze congruenti FL = LQ e [EF =] FG > QR (QR contenuto in
FG). Quindi l'area di EFLI è maggiore di quella di LQRM e, per simmetria [LA
SIMMETRIA DI ...], la tesi.
L'area del quadrato inscritto è 1/2 di quello assegnato, poiché EF = AC/2,
essendo la congiungente i punti medi dei lati del triangolo ABC e quindi l'area
di EFGH = EF^2 = (AC^2)/4, mentre l'area di ABCD = (AC^2)/2.
| Home Page Cabri | Torna a FLATlandia | Archivi |