 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Novembre 1999
Il testo del problema:
a) Costruire un triangolo isoscele la cui base sia metà del lato. Motivare la costruzione.
b) Dimostrare (ricorrendo eventualmente ad una opportuna costruzione) che la bisettrice di un angolo alla base del suddetto triangolo taglia il lato opposto in due parti una doppia dell'altra.
Nota: gli allievi della scuola media inferiore non erano tenuti a rispondere alla parte b).
Per il problema di Novembre 1999 abbiamo ricevuto ventitre risposte
provenienti da: dieci scuole superiori, sei scuole medie, una scuola
elementare; due risposte non forniscono indicazioni sulla scuola e/o sulla
classe.
Il problema proposto richiedeva a tutti la costruzione di un
particolare triangolo isoscele e ai ragazzi delle superiori la
dimostrazione di una sua proprietà.
Abbiamo ricevuto due risposte complete anche da due scuola medie inferiori,
la "Don Bosco" di Padova e la Scuola Media di Roveredo; ci
complimentiamo con loro.
Un ragazzo della scuola media "Vochieri" ha fatto una
costruzione secondo una congettura che non ha giustificato: abbiamo pensato di
proporla ugualmente, perché può essere interessante per gli altri trovarne la
dimostrazione.
Ricordiamo ai ragazzi delle scuole medie che le costruzioni richieste vanno
sempre giustificate, anche se appaiono "evidenti". Ricordiamo anche
che due circonferenze secanti o una circonferenza e una retta secante, hanno due
punti in comune ed è corretto citarli entrambi.
Fra le risposte inviate dai ragazzi delle superiori tre non sono accettabili
perché presentano gravi imprecisioni o incompletezze nella seconda parte. Le
risposte con indicazioni incomplete non verranno riportate anche se corrette.
Un'ottima soluzione è giunta da una classe terza liceo scientifico di Roma:
l'abbiamo valutata ma non verrà presentata essendo FLATlandia un'attività
rivolta ai ragazzi del biennio di scuola superiore.
Fra le soluzioni accolte si evidenziano ben cinque tipi di dimostrazioni, svolte
tutte in modo sostanzialmente corretto nel contenuto. Questo ci mette
nell'imbarazzo della scelta di quelle da presentare.
Abbiamo adottato, quando possibile, il criterio di scegliere le risposte delle
scuole "nuove" per dar loro il benvenuto nel mondo di FLATlandia
e di citare quelle analoghe.
Per quanto riguarda la forma, RIBADIAMO di attenersi alle istruzioni indicate
nella premessa ad ogni problema.
Le scuole che hanno partecipato sono:
Riportiamo qui di seguito:
E più in basso, complete di immagini:
NOTA: Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre.
Alessio Miceli
Scuola Media "A.Vochieri" - Alessandria
Ho costruito il triangolo isoscele con la base uguale a ½ [un mezzo] del
lato in questo modo:
Circonferenza raggio OS
Punto medio P del raggio
Circonferenza di raggio SP
Punti di intersezione A-B tra le due circonferenze
Retta per OS
Punto di intersezione C tra la retta e la circonferenza
Triangolo ABC
Ho fatto questa costruzione sulla base di questo ragionamento:
Per costruire un triangolo equilatero(base congruente con i lati) devo [posso]
intersecare due circonferenze che hanno lo stesso raggio, quindi per ottenere un
triangolo con la base uguale a un mezzo del lato devo [posso] dimezzare il
raggio di una circonferenza. Ho controllato le misure con "Distanza e
lunghezza" e ho verificato che corrispondevano all'ipotesi da verificare.
Acazi Martina e Manci Mariachiara
Classe II media sez. A
Scuola Media "Don Bosco" - Padova
a) Traccio una circonferenza con centro O e un suo diametro AB, quindi una
retta passante per O. Traccio il segmento AO, raggio della circonferenza e base
del triangolo isoscele.
Punto il compasso in A e traccio un archetto con apertura AB. Ripeto puntando il
compasso in O. Chiamo C il punto d'incontro degli archetti. Il triangolo AOC
risulta essere isoscele perchè i suoi due lati AC e OC risultano congruenti al
diametro AB (AB = 2AO).
b)Traccio la bisettrice dell'angolo A, chiamo M il puno d'incontro di questa
con il lato CO. Traccio il segmento CB e considero il triangolo ABC: esso
risulta isoscele, poichè AB = AC. Chiamo L il punto d'incontro tra la
bisettrice e il lato CB: Poiché il triangolo ABC è isoscele e CB è la sua
base, AL oltre che bisettrice risulta essere anche mediana rispetto al lato
CB.
Anche CO è mediana rispetto al lato AB, per quando già detto prima. Il punto M
è dunque il baricentro del triangolo, un punto notevole dei triangoli che ha la
proprietà di dividere le mediane in due parti una doppia dell'altra.
Quindi CM = 2MO.
Urzì Daniele
Classe II sez. B
Liceo Scientifico "G.Galilei" - Catania
a) Sia AB un segmento; esso sarà la base del triangolo
isoscele che vogliamo costruire.
Chiamiamo r l'asse di AB, poiché ogni punto di r
è equidistante da A e da B il vertice del
triangolo richiesto si trova su r.
Puntando il compasso in A e in B e con apertura
uguale a due volte AB, tracciamo un arco che intersecherà r in C;
congiungiamo C con A e B, essendo
CA=CB=2AB la costruzione è completa.
b) Tracciata la bisettrice dell'angolo BAC sia
D il suo punto di intersezione con il lato BC .Chiamiamo
E ed F i punti medi di CD e CA
rispettivamente; il segmento FE sarà parallelo al lato AD (perché
è il segmento che unisce i punti medi di due lati di un triangolo).
Si prolunghi ora il lato CA di un segmento AP=AB e
si congiunga P con B. Il triangolo APB è isoscele su base PB,
pertanto gli angoli alla base sono uguali. L'angolo CAB è esterno
rispetto al triangolo APB, avremo cosi' CAB= APB+ PBA = 2PBA; questo
significa che CAB=ABP e di conseguenza le rette PB
e AD sono parallele perché tagliate dalla trasversale
AB formano angoli alterni interni eguali.
Se adesso consideriamo il fascio di rette parallele FE, AD, PB
tagliato dalle trasversali CP e CB avremo, per il
teorema di Talete che a segmenti eguali sulla prima trasversale, CF=FA=AP,
corrispondono segmenti uguali sulla seconda trasversale: CE=ED=DB,
pertanto è CD=2DB.
Classe
V
A
Liceo
Classico
S.
Weil
- Treviglio
(BG)
A)
Dato un segmento AB, tracciare una circonferenza di raggio AB [con centro in B]
e prolungare il segmento fino ad incontrare la circonferenza nel punto C.
Tracciare
una circonferenza di centro A e di raggio AC e poi un'altra circonferenza di
centro B e di ugual raggio.
Considerare
uno dei due punti d'intersezione D delle circonferenze tracciate (di ugual
raggio) e congiungerlo con i punti A e B.
Si ottiene così un triangolo con il lato AD=DB=2AB.
IL punto B è stato risolto dall’alunna Linda Vitali.
B)
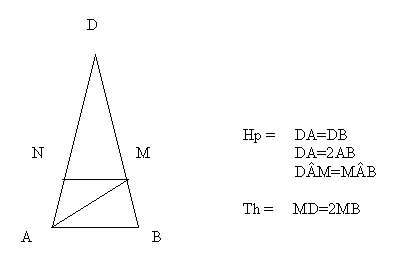
Tracciare NM parallelo ad AB.
Si ottiene così un triangolo DNM simile al triangolo ABD: i due triangoli hanno
gli angoli omologhi congruenti in quanto hanno l'angolo ADB in comune e gli
angoli alla base corrispondenti rispetto alle rette // MN e AB tagliate dalle
trasversali DA e DB.
Di conseguenza DN=2NM.
L'angolo NMA è uguale all'angolo MAB perché alterni interni, quindi il
triangolo ANM è isoscele perché l'angolo NMA è uguale all'angolo MAN [per
proprietà transitiva].
Quindi ND=2AN e DM=2MB.
Moscatelli Marco, Urbano Sara, Ventura Daniela
Classe 2A - Liceo Scientifico Tecnologico dell'Istituto Tecnico Industriale
e Liceo Scientifico Tecnologico "Cartesio" di Cinisello Balsamo (MI)
a) Costruzione del triangolo isoscele di base pari a metà del lato.
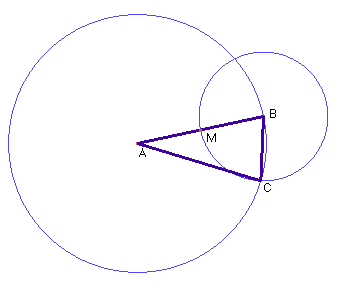
È dato il segmento AB lato del triangolo isoscele
Si traccia la circonferenza di centro A e raggio AB
Si individua il punto medio M del segmento AB
Si traccia la circonferenza di centro B e raggio BM
Si individua uno dei due punti di intersezione tra le circonferenze (denominato con C)
Si traccia il segmento AC, che essendo raggio della prima circonferenza sarà congruente ad AB
Si traccia il segmento BC che essendo raggio della seconda circonferenza sarà congruente a BM e perciò pari alla metà di AB, come richiesto.
b) dimostrare che la bisettrice di un angolo alla base del suddetto triangolo taglia il lato opposto in due parti una doppia dell'altra.
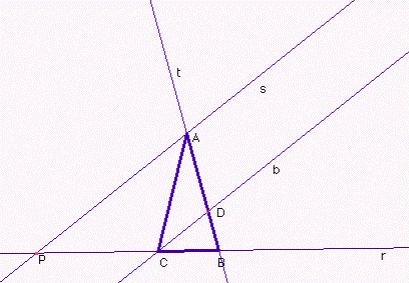
Si traccia la retta r di sostegno della base BC
Si traccia la bisettrice b dell'angolo alla base in C
Si indica con D il punto di intersezione con il lato opposto AB
Si traccia la retta t di sostegno al lato AB
Si traccia la parallela s, passante per A, alla bisettrice b
Si indica con P il punto di intersezione tra le rette s e r
Il
triangolo ACP è isoscele con base AP in quanto:
- Gli angoli CAP e ACD sono congruenti perché alterni interni
- Gli angoli DCB e APC sono congruenti perché corrispondenti
- Gli angoli DCB e ACD sono congruenti per costruzione
- Di conseguenza gli angoli APC e CAP, per transitività sono congruenti
Considero le parallele s, b e le trasversali r, t: per il Teorema di Talete CP:CB=AD:DB, inoltre siccome CP è congruente a AC si ha che AC:CB=AD:DB, inoltre AC è congruente al doppio di BC, si ha che 2BC:BC=AD:DB
Di conseguenza il rapporto tra AD e DB è 2 c.v.d.
Gruppo
di studenti delle seconde classi
Liceo Scientifico "G. Galilei" - Bitonto
A)
COSTRUZIONE
- Costruire un segmento EF;
- individuare il suo punto medio G
- Individuare una semiretta Ar nel piano
- Tracciare col compasso una circonferenza di centro A e di raggio EG
- Sia C il punto di intersezione tra tale circonferenza e la semiretta Ar
- Tracciare col compasso una circonferenza di centro A e di raggio EF
- Tracciare un'altra circonferenza di centro C e di raggio EF
- Individuare il punto di intersezione B tra le due circonferenze
- Costruire il triangolo ABC isoscele in quanto AB=BC=EF e con base AC=EG=1/2*EF=1/2*AB
per costruzione .
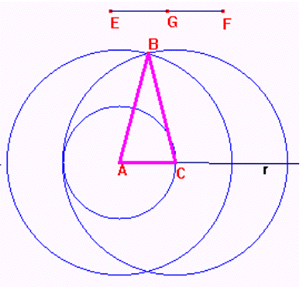
B) Prima risoluzione
Tracciare la bisettrice r dell'angolo ACB; sia I il punto d'intersezione di r con AB; condurre la parallela s ad r passante per il punto medio N di BC e sia L la sua intersezione con AB. Essendo BN congruente a CN, per Talete applicato alle rette parallele r ed s e alle trasversali BC e BA, BL è congruente a LI. Congiungere A ad N e considerare il triangolo ACN isoscele poichè AC è congruente a CN per ipotesi. Per la proprietà dei triangoli isosceli, CH, dove H è il punto d'intersezione fra CI ed AN, è sia bisettrice che mediana relativa alla base, per cui AH è congruente ad HN. Considerando le rette parallele r e s e le trasversali AB e AN, per Talete, LI è congruente ad AI e per transitività ad LB.
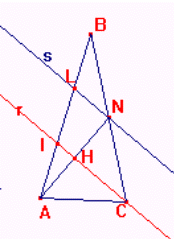
B) Seconda risoluzione
H: ABC isoscele su AB;
AB=1/2CA;
AD bisettrice dell'angolo CAB.
T: DB = 1/3CB
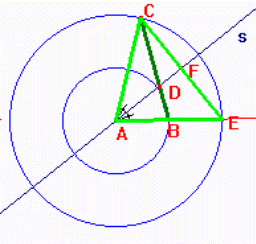
Dimostrazione
-Costruire la bisettrice s dell'angolo CAB;
- sia D il punto intersezione fra il lato obliquo CB e la bisettrice;
- considerare il triangolo ACE isoscele su CE, essendo AC = AE raggi della
stessa circonferenza;
in esso AF, in quanto bisettrice dell'angolo al vertice, è anche mediana
relativa alla base;
CB è la mediana di ACE relativa ad AE, perchè AB = BE per costruzione;
essendo AF e CB mediane del triangolo e D il loro punto intersezione, D è il
baricentro del triangolo ACE e quindi divide CB in parti tali che CD = 2DB
| Home Page Cabri | Torna a FLATlandia | Archivi |