 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Marzo 2000
Il testo del problema:
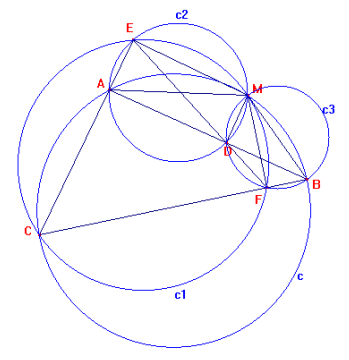
Dato un triangolo ABC costruire la circonferenza c ad esso
circoscritta, e da un punto M dell'arco AB di essa mandare le perpendicolari MD,
ME, MF rispettivamente sui lati AB, AC, BC .
Tracciare poi i segmenti MA e MB.
a) Trovare nella figura così formata quattro
quadrilateri inscrittibili.
b) Confrontare gli angoli AMB e EMF, poi gli angoli AME e BMF.
c) Dimostrare che i punti D, E, F sono allineati.
Motivare le risposte.
COMMENTO
Abbiamo ricevuto quindici risposte provenienti da dieci scuole. Quattro sono
scuole medie inferiori e sei risposte provengono da una stessa classe di scuola
media che si è organizzata in gruppi e ciascuno di essi ha inviato il suo
elaborato. Purtroppo non tutto il loro lavoro è accettabile, auguriamo a questi
ragazzi un miglior esito con i prossimi problemi.
Una scuola media non ci ha fatto pervenire il suo nome quindi non potrà essere
menzionata.
Il problema di marzo conduceva attraverso tappe successive alla scoperta
della cosiddetta retta di Simson.
La dimostrazione dell'allineamento di tre punti è una questione un po' delicata
che spesso trae in inganno: per questo ci è sembrato utile proporla almeno una
volta nei problemi di Flatlandia.
Fra le risposte pervenute dalle scuole superiori solo tre sono completamente accettabili anche se non è stata sempre citata la costruzione della circonferenza circoscritta; due sono incomplete in molte parti e una non è valida per diversi motivi:
Per quanto riguarda le scuole medie inferiori, due hanno risposto in modo
apprezzabile anche se incompleto ai punti (a) e (b) e una in modo completo al
punto (a). Le altre risposte non sono accettabili in quanto si limitano ad
elenchi o descrizioni senza alcuna giustificazione o con giustificazioni errate.
A chi ha provato a dimostrare il punto (c) dobbiamo far notare che la figura
EMFD non può essere vista come un triangolo finché non si e' dimostrato
l'allineamento dei tre punti E,D,F.
Le scuole che hanno partecipato sono:
Riportiamo la soluzione del liceo Galilei di Bitonto perché più completa anche se simile a quella del Galilei di Catania, e la soluzione dell'ITI Berenini, che si differenzia nella terza parte dalla precedente.
Soluzione proposta da
Gruppo di studenti delle seconde classi
Liceo Scientifico "G.Galilei" - Bitonto (BA)
Dato il triangolo ABC si costruisce la circonferenza c ad esso circoscritta
tracciando gli assi dei tre lati individuando in tal modo il circocentro O.
Tracciati i segmenti e le perpendicolari richiesti dalla traccia le risposte ai
3 punti sono le seguenti:
a) I quattro quadrilateri inscrittibili sono:
1) MACB perché inscritto nella circonferenza c;
2) MEAD perché gli angoli opposti MEA e MDA sono entrambi retti per
costruzione, soddisfacendo in tal modo la condizione necessaria e sufficiente di
inscrittibilità di un quadrilatero;
3) MFCE perché gli angoli opposti MFC e MEC sono entrambi retti per
costruzione;
4) MDFB è inscritto nella semicirconferenza c' di diametro MB in cui sono
inscritti i triangoli rettangoli MDB e MFB aventi la stessa ipotenusa MB.
b) Gli angoli AMB e EMF sono congruenti perché entrambi supplementari di BCA,
il primo nel quadrilatero AMBC e il secondo in EMFC;
AME=FME-FMA, BMF=BMA-FMA e quindi AME e BMF sono angoli congruenti per
differenza di angoli congruenti;
c) 1) BMF=BDF, perché angoli alla circonferenza c' che insistono sullo
stesso arco BF;
2) MDE=MEA[MAE], perché angoli alla circonferenza di diametro MA che insistono
sullo stesso arco ME;
3) AME=BMF perché dimostrato nel punto b);
4) AME+EAM=90° perché angoli acuti del triangolo rettangolo EAM;
5) MDB=90° per costruzione;
Dai punti precedenti segue che EDF=EDM+MDB+BDF=180° e quindi i punti E, D ed F
sono allineati.
Soluzione proposta da
Studenti della 1B dell'indirizzo scientifico tecnologico
ITIS "Berenini" di Fidenza (PR)
Innanzitutto precisiamo che abbiamo considerato il punto M sull'arco AB che non contiene C, anche se il testo non lo precisava esplicitamente.
a) Un quadrilatero inscrittibile è certamente AMBC in quanto
per costruzione ABC sono punti della circonferenza c e M è un punto dell'arco
AB della medesima circonferenza c.
Inoltre, poiché condizione necessaria e sufficiente affinchè un quadrilatero
sia inscrittibile in una circonferenza è che gli angoli opposti siano
supplementari, si trovano i seguenti quadrilateri inscrittibili:
EMFC è inscrittibile nella circonferenza c1 in quanto ha gli angoli opposti MEC
e MFC retti e quindi supplementari AEMD è inscrittibile nella circonferenza c2
in quanto ha gli angoli opposti MEA e MDA retti e quindi supplementari.
Inoltre i triangoli BMD e BMF sono rettangoli rispettivamente in D e in F
pertanto entrambi inscrittibili nella stessa semicirconferenza di diametro BM e
quindi il quadrilatero DMBF è inscrittibile in una semicirconferenza e quindi
anche in una circonferenza (c3).
b) Gli angoli AMB e EMF sono congruenti perché entrambi supplementari
dell'angolo ACF ( in quanto opposti rispettivamente nei quadrilateri inscritti
AMBC e EMFC ).
Anche gli angoli AME e BMF risultano congruenti perché si ottengono sottraendo
l'angolo AMF rispettivamente dall'angolo AMB e dall'angolo EMF che come detto
sopra sono congruenti.
c) Per dimostrare che D,E,F sono allineati è sufficiente dimostrare che gli
angoli EDA e BDF sono congruenti.
A tal fine osserviamo che l'angolo EDA e l'angolo EMA sono congruenti perché
sono angoli alla circonferenza c2 che insistono sullo stesso arco EA.
L'angolo EMA e l'angolo BMF sono congruenti per quanto affermato al punto b).
Inoltre l'angolo BMF e l'angolo BDF sono congruenti in quanto angoli alla
circonferenza c3 che insistono sullo stesso arco BF. Quindi per la proprietà
transitiva della congruenza l'angolo EDA risulta congruente all'angolo BDF e
quindi essendo A,D,B allineati risulta che anche D,E,F sono allineati.
| Home Page Cabri | Torna a FLATlandia | Archivi |