 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Maggio 2000
Il testo del problema:
Siano A, B, C, D i vertici di un parallelogramma nominati in verso antiorario. Sia I un punto qualunque della diagonale BD. Sia EF il segmento per I parallelo al lato AD che ha gli estremi E ed F che appartengono rispettivamente ai lati AB e CD. Sia GH il segmento per I parallelo al lato AB con gli estremi G ed H che appartengono rispettivamente ai lati AD e BC.
a) Dimostrare che dei quattro parallelogrammi che si formano quelli attraversati dalla diagonale sono simili.
b) Supposto che l'angolo ABC sia retto e che il segmento BI sia la terza parte di BD stabilire il rapporto delle aree dei parallelogrammi AEIG e CFIH.
c) Rispondere alla domanda del punto precedente nel caso in cui l'angolo ABC non sia retto ed I sia un punto qualunque della diagonale BD.
COMMENTO
Questo mese abbiamo ricevuto undici risposte provenienti da dieci scuole, fra
le quali due scuole medie e una scuola elementare. E' giunta una ulteriore
soluzione inviata da parte di alcuni allievi di una classe terza di liceo
scientifico cui abbiamo risposto a parte in quanto l'attività di Flatlandia
è rivolta agli studenti della scuola media e del biennio di scuola superiore.
Ci complimentiamo con le quinte classi del Circolo Didattico di Alessandria per
il lavoro da loro svolto, anche se largamente carente nelle giustificazioni.
Le scuole che hanno partecipato sono:
Il problema di questo mese non presentava particolari difficoltà: si trattava di esaminare i legami fra le figure ottenute scomponendo un parallelogrammo con due rette parallele ai lati ed intersecantisi su una diagonale. In effetti, come è stato rilevato in alcune risposte, il punto b) era un caso particolare del punto c) e presentava addirittura dei dati superflui.
In tutte le risposte pervenute il problema è stato risolto: qualcuno si è dilungato eccessivamente nelle giustificazioni, qualcuno e' invece stato troppo conciso a scapito della completezza; l'esposizone è in generale buona, pochi gli errori rilevati, dovuti soprattutto a distrazione.
Si sono delineate sostanzialmente due tipi di soluzioni sia per il punto a), in cui sono stati utilizzati il teorema di Talete o la similitudine di triangoli, sia per le parti b) e c), in cui sono stati utilizzati l'equiscomponibilità di figure o il calcolo delle aree.
Riportiamo la risposta della SM di Roveredo, citando quelle simili, la risposta dell'ITI "Berenini" (prima e seconda parte) e un commento al punto b) di Daniele Urzi', LS "G. Galilei" di Catania.
Riportiamo inoltre la figura animata dell'ITI "Berenini" e la risposta dell'ITI "Ferrari", simile nelle parti b) e c) a quelle inviate dal LS "Galilei" di Adria.
NOTA: le correzioni o i commenti al testo sono riportate in parentesi quadra.
Soluzione proposta da:
CLASSE 2^ A - Scuola Media Statale di Roveredo in P. (PN)
(Sezione Staccata della S.M.S. "G. Zanella" DI Porcia)
[Soluzioni simili a questa sono state inviate dagli allievi
dell'ITG "Buonarroti", del LS "G. Galilei" e dell' ITG
"Rondani"]
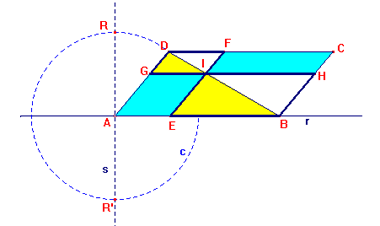
( r ed s sono rette perpendicolari passanti per A, centro della circonferenza
c;
D si muove lungo la circonferenza c, quando coincide con R o R' il
parallelogramma si fa rettangolo;
I si sposta lungo il segmento DB )
a)
c)
b)
Soluzione proposta da
Paolo Guasti, Jacopo Guarneri, Massimiliano Montuschi e Gian Luca Zuccheri
classe 1°B dell'indirizzo scientifico tecnologico - scuola ITIS "BERENINI"
di Fidenza.
a)
Le figure DGIF e IEBH sono parallelogrammi perché hanno coppie di
lati opposti paralleli.
Inoltre l'angolo GDF è uguale all'angolo EIH perché sono entrambi
corrispondenti dell'angolo AGI.
L'angolo DFI è uguale ad IHB perché corrispondente di DCB.
Perciò i due parallelogrammi hanno angoli congruenti.
GIF è congruente a GDF perché sono angoli opposti di un parallelogramma e EBH
è congruente a EIH perché sono angoli opposti di un parallelogramma; quindi,
per la proprietà transitiva, GIF è congruente a EBH ; analogamente si prova
che DGI è congruente a IEB.
Inoltre le coppie di lati che comprendono angoli congruenti sono proporzionali,
infatti, utilizzando il teorema di Talete nel fascio di rette AB // GH // DC
tagliate da AD e DB e nel fascio di rette AD // EF // BC tagliate da AB e DB, si
ottengono rispettivamente le seguenti proporzioni:
GD: DI = AG: IB
AE: DI = EB: IB
GD: AG = AE: EB, ma essendo AG = EI e AE= GI (segmenti paralleli compresi tra
rette parallele)si ottiene GD: AI =GI: EB.
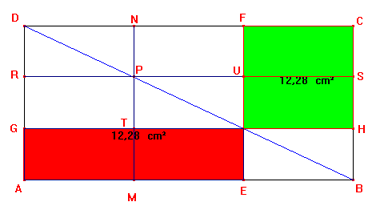
b)
I parallelogrammi AEIG IHCF che in questo caso sono rettangoli, hanno aree uguali perché se si considera il punto P di DB tale che PB= 2/3 DB e da esso si conducono il segmento RS // AB e il segmento MN // AD, detti T e U rispettivamente le intersezioni di MN con GH e EF con RS, i rettangoli AEIG e IHCF risultano scomposti in due rettangoli congruenti perchè AM =ME =EB =IH =US =1/3 AB e MT=ET=IU=FU=1/3 BC sempre grazie al teorema di Talete. Pertanto le aree di AEIG e IHCF sono uguali e quindi il loro rapporto è 1.
c)
NOTA: qui sotto vedete l'immagine statica, è disponibile la VERSIONE ANIMATA CABRIJAVA selezionando la figura.
Commento al punto b) proposto da:
Daniele Urzì - Classe II B
Liceo Scientifico "G.Galilei" Catania
Nel punto b) si ha che BI =(1/3) DB. Dalla similitudine dei triangoli
DGI ed IEB si ricava che il rapporto fra le superficie dei rettangoli DGIF e
IEBH è uguale a 4.
In generale è facile dimostrare che se la diagonale BD viene divisa in n parti
uguali ed è BI = (1/n) BD il rapporto tra i rettangoli sopra indicati è uguale
a (n-1)^2.
Soluzione proposta da:
Alberto Boscaggin
Classe 2a A st ITIS E. Ferrari ( TO )
a)
Il triangolo EIB è simile al triangolo ABD, poiché EI è parallela a AD Il
triangolo GID è simile al triangolo ABD, poiché GI è parallela a AB.
Quindi EIB è simile GID.
Essendo EIHB e GIFD due parallelogrammi, i lati opposti sono congruenti. I due
parallelogrammi hanno quindi [gli angoli uguali e] i lati ordinatamente in
proporzione, per cui sono simili.
b)
Il triangolo ABD è simile al triangolo EBI.
Il loro rapporto di similitudine è BD / IB, cioè BD / ( 1/3 * BD ), cioè 3
Quindi AB = 3 EB, cioè AB = 3 IH, da cui IH = 1/3 * AB
AD = 3 IE, cioè AD = 3 AG, da cui AG = 1/3 * AD
Il triangolo ABD è simile al triangolo GID
Il loro rapporto di similitudine è BD / ID, cioè BD / ( 2/3 * BD ), cioè 3 /
2
Quindi AB = 3 / 2 * GI, cioè AB = 3 / 2 * AE, da cui AE = 2 / 3 * AB
AD = 3 / 2 * GD, cioè AD = 3 / 2 * IF, da cui IF = 2 / 3 * AD
Il rapporto tra le aree è dato da ( AE * AG ) / ( IH * IF )
Sostituendo i valori trovati, abbiamo
( 2 / 3 * AB * 1 / 3 * AD ) / ( 1 / 3 * AB * 2 / 3 * AD ) = 1
c)
Il triangolo GID è simile al triangolo EBI.
Il loro rapporto di similitudine è ID / IB.= k
Quindi GI = k * EB, cioè AE = k * IH
Indichiamo con m [la misura del]l'altezza di GID relativa al lato GI e con n [la
misura del]l'altezza di EBI relativa a EB
Quindi m = k * n.
Il rapporto tra le aree dei due parallelogrammi è ( AE * n ) / ( IH * m ).
Infatti l'altezza di AEIG è congruente all'altezza di EBI e l'altezza di CFHI
è congruente all'altezza di GID. ( sono la distanza tra rette parallele ).
Sostituendo, abbiamo ( k * IH * n ) / ( IH * k * n ) = 1
| Home Page Cabri | Torna a FLATlandia | Archivi |